
はじめに
今回は万有引力の問題を解くためのポイントを確認していきます。
万有引力の問題の解法は、結論から先に言ってしまうと、物体がとる軌道によって解法が決まってきます。まずはそういったところの確認を行ってから、実際に問題を解いてみようと思います。
これから確認するポイントは3つあります。
①:地球上で受ける万有引力が重力であること
②:万有引力の問題の解法について
③:第1宇宙速度と第2宇宙速度について
それでは、順番に見ていきます。
1.地球上では「万有引力」=「重力」
まず1つ目ですが、物理基礎で学習してきた地球上の物体にはたらく重力mgという力は、実は、地球から受ける万有引力のことであったということです。

したがって、質量mの物体が受ける重力は重力加速度をgとすると、mgとなるわけですが、万有引力定数をG、地球の質量をM、半径をRとすると、万有引力は
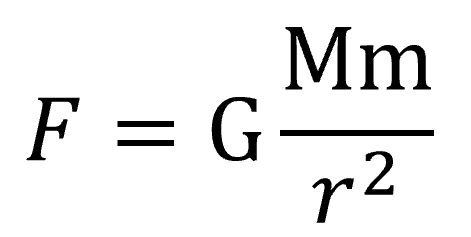
となって、これが高校物理では、重力mgと同値であるというわけです。

この式は、力のつり合いを示しているわけではないので注意してください。
重力と万有引力がつり合っているわけではありません。
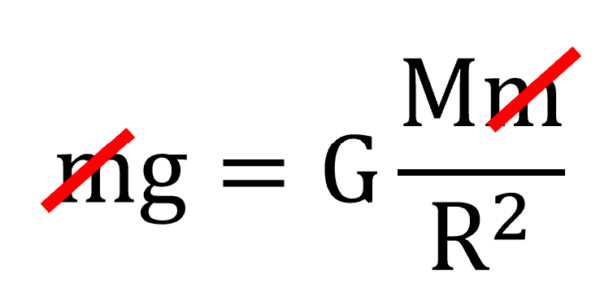
それで、両辺にあるmを消去して、この式の右辺を見ていきたいのですが、

Gは定数です。Mは地球の質量だから定数、地球の半径だからRも定数です。
これが全て定数ということは、これらを計算した結果も定数になります。

つまり、重力加速度gというのは、地球上の万有引力の定数部分を1つの文字に置き換えたものと言えるわけです。
実際に、GとMとRの値を代入して計算してみると、確かにg=9.8という結果が出てきます。

地球が自転していることを考慮すると、実際の重力加速度は、これよりもう少し小さくなるわけですが、問題を解く時には、地球上の万有引力と重力が等しいものとして取り扱います。
2.万有引力の解法
それでは、2つ目のポイントに移ります。冒頭でも述べた通り、万有引力の解法は、物体がとる軌道が円軌道かどうかによって決まります。
円軌道の場合
まずは、円軌道からですが、前回の講義でケプラーの法則であったり、万有引力による位置エネルギーの話をしました。
円軌道においても、これらは成立するのは当然なのですが、円軌道、つまり等速円運動している場合だと、速さは一定だから、例えば、面積速度が異なる2か所で同じであると言ったところで、問題を解くうえでは何の手掛かりにもなりません。

エネルギー保存則についても確かに成立はします。しかし、地球からの距離が常に変化しなかったら、そこから速度が求めることが出来ません。
つまり、円軌道の問題では、エネルギー保存則、面積速度一定の法則は成り立ちますが解法としては使えません。

そこで、ここでは運動方程式を立てることを考えていきます。物理基礎の範囲では、運動方程式から求められるのは、せいぜい力であったり加速度だけになるわけですが、等速円運動では、加速度がr分のv2であったり、rw2と特別な表記を持っています。

特別な表記を持っているが故に、rが分かればvがわかり、vが分かればrがわかり、wがわかればrがわかるというように、どちらか一方がわかれば、もう一方がわかってくるわけです。
また、vとwが分かっていれば、こちらの式から、軌道の周期がわかります。
円軌道以外の解法

それでは円軌道以外の軌道だったらどうするのか??
例えば楕円軌道だと、加速度の表し方がわからないので、高等学校の範囲では運動方程式は使えません。しかし、この時は逆にケプラーの法則であったり、エネルギー保存則が生きてきます。
次回の記事では、こういったことを押さえながら解説を行っていきます。
第1宇宙速度と第2宇宙速度
それでは最後に3つ目のポイントです。
第1宇宙速度と第2宇宙速度。

この2つの言葉は覚えてもらった方がいいと思います。
第1宇宙速度は、地球表面すれすれの円軌道を回る物体の最小初速度のことで、大気の影響などを受けない前提で、地球表面から物体を打ち出した時に、地球すれすれを回る物体の速度のことです。

要は、これより速度が小さいと地面に激突してしまうという訳です。
一方、第2宇宙速度とは、地上から無限遠方へ物体を飛ばすための最小初速度で、物体をある速度で飛ばした時に、はるか無限遠で静止する。そんな速度のことです。

つまり、物体を打ち出した時に、第1宇宙速度より小さければ、地面に激突しますが、大きすぎると、はるか彼方に飛び去って戻って来なくなるわけです。
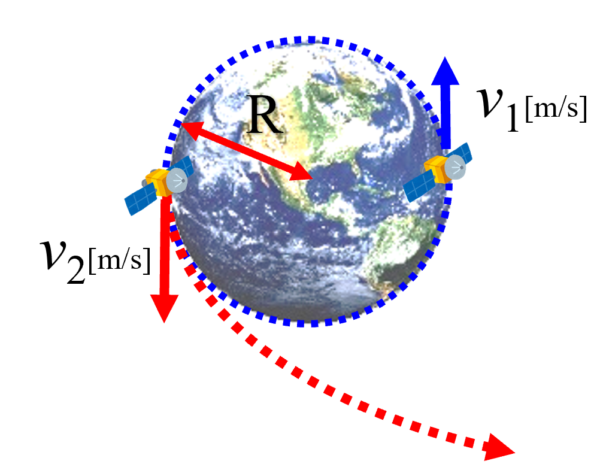
この第1宇宙速度と第2宇宙速度は、地球の半径をR、質量M、万有引力定数をGとすれば実際に求めることが出来ます。第1宇宙速度v1は、運動方程式より質量m[kg]の物体に加速度aを与えたのは万有引力であり、ここで等速円運動をしているので加速度の表記はR分のv12となって、v1を求めると次のようになります。
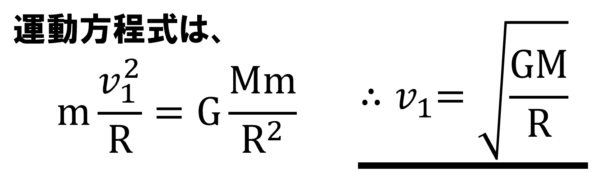
第2宇宙速度v2は、とても大きな負の位置エネルギーをゼロにするためには、とても大きな運動エネルギーを与えないといけませんから、次のような式から求められます。
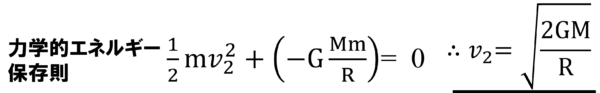

これは前回の講義でやりました。
第1宇宙速度と第2宇宙速度はルート2倍しか違わないというのは面白い結果です。速度が小さいと、宇宙に飛び立つことが出来ませんが、大きすぎるとどっかへ飛んで行ってしまって戻ってこない。その速度の違いがたったの1.4倍程度である。

無人ロケットを飛ばすのであればまだしも、人が乗ってたりしたら大変なことです。
こうして、第1宇宙速度と第2宇宙速度を求めたわけですが、先ほど説明した円軌道の解法にあてはまっていることを確認してください。第1宇宙速度は、円軌道なので、運動方程式を使いました。第2宇宙速度は円軌道ではないので、エネルギー保存則を使っています。



















