
偏差値競争によって強いられた学習習慣は物理教育を困難にする。
次の文章は、
の宿題に関する記述を抜粋したものである。
まずこちらから目を通していただきたい。
1.学生たちの授業に対する意識と物理の問題を解く実力について
【抜粋1】
私の経験では、あまりに多くの学生が、物理とは単純な事実の集合と一連の方程式からなっており、それらを覚えさえすれば、私の授業で評価Aがとれると期待している。
逆に、物理について深く考え、強固な概念的理解と適切でよく組織された知識を構築しなければ解けないような複雑な問題を解くことができる学生は、きわめて少ない。
宿題は学生に物理を学ばせるうえで大きな価値をもちうるが、悪い宿題は逆に、「事実と方程式で充分だ。」という見方を補強するような、悪いメッセージを送ってしまう。
不幸にして、ときには最善の努力をつくしたにもかかわらず、悪いメッセージが伝わってしまうのだ。
【抜粋1終了】
※ここでは、複雑な問題を解くことが出来る学生は少ない、とした上で宿題が大きな価値を持つと主張するが、宿題の内容設定によっては、悪い効果を生むと警告している。
2.悪い宿題が学生に与える弊害
【抜粋2】
私の授業が目指しているものは、単に数値を代入して計算することだ、と思う(あるいは望む)ようになるのだ。これは、そのような問題であれば彼らが快適に解けることから生まれる、かなり標準的な願望的観測である。
もしも彼らが質問に対して適当なことを書き連ね、計算問題の全部に正解し、推論問題に対して部分点をもらうのに充分な程度のことが書ければ、この課題について必要なことは全部わかったのだと、満足してしまうのだ。質問は、学生に概念について深く考えさせることを想定しており、推論問題は、物理をどう適用すればよいかについてしっかりと理解させるものとされている。しかし、計算問題という抜け穴を与えてしまうと、学生の中には、それを解く以上のことはしようとしないものが出てくる。
もしも彼らが質問に対して適当なことを書き連ね、計算問題の全部に正解し、推論問題に対して部分点をもらうのに充分な程度のことが書ければ、この課題について必要なことは全部わかったのだと、満足してしまうのだ。質問は、学生に概念について深く考えさせることを想定しており、推論問題は、物理をどう適用すればよいかについてしっかりと理解させるものとされている。しかし、計算問題という抜け穴を与えてしまうと、学生の中には、それを解く以上のことはしようとしないものが出てくる。
【抜粋2終了】
※悪い宿題が与える弊害として、物理の問題は単に数値を代入して計算することだと学生が思うようになるとして、これについては、宿題の中に推論問題が含まれていても、計算問題を与えてしまうと、学生たちに逃げ道を与えて、推論問題を深く考えないきっかけを作ってしまう。
3.物理の問題を解くために必要な力
【抜粋3】
現実的な物理の問題を解くときの一番の難しさは、現実世界の複雑な状況の中から、解くことができる物理の問題を抽出することにある。問題の状況の中に現れる量に変数名をつけてしまったり、問題に関係する量についてだけ言及して無関係なことを省いてしまったり、何が重要で何がそうでないかの選択が明白になるように問題を設定してしまうと、私たちは
学生から、広範な本質的な問題解決スキルを学習する機会を奪ってしまうことになる。
【抜粋3終了】
※これは他の科目についても共通するところがあると思う。
学問に励むことによって、身につけた教養は、現実世界の複雑な状況を吟味して、問題の本質を明確にし、解消すべき問題点を抽出し、優先順位の高いものから順に解決に向けて着手する能力を与えてくれる。
(これを論理的思考力とここでは呼ぶことにする。)
論理的思考力は、社会生活を営む上で大変重宝される能力だと思うのだが、世間一般を見渡して、この力を備えている人が非常に少ないように感じる。
(私自身、論理的思考力とは何かということを数年前に自分なりに理解しつつある段階なので、はっきり言って、私にもその力が十分身についているかと言われれば、そうではないと思う。)
などから、学生の読解力が低いことを知ると、読書の好き嫌いや家庭での学習習慣が読解力との相関性がないという情報はスルーして、おそらく教育現場では、朝読(※1)を取り入れようとするだろう。
※1朝読:朝の連絡会から授業の合間などの隙間時間に全員で一斉に読書を行うことを指す。
読み解く力(=読解力)が低いとなった時に、多くの人が読書の時間を増やそうと量でカバーしようとする。
問題が仮に、語句と語句のつながりや各文章や段落のつながりにおける論理性を吟味して、全体として著者が何を伝えたいのかを読み解く力が足りないとする。それを解決するために、朝の読書習慣を取り入れたとしても、小説を読んで、登場人物に独自の感情移入をするだけでは、目的とする成果は得られない。
そもそも学生たちは、論理的思考力はおろか、読解力を身に付ける術をしらないから、読解力が低いのである。量的な手段に着手する前に、質的な手段、つまりこの場合だと、適切な文章の読み方からまず伝授しないといけない。
ここから本題に入るが、上記の様な問題が、物理教育をいっそう困難にさせている。
そして、
過度な偏差値至上主義ともとれる他校との競争意識が、さらに問題を深刻化させている。
大学進学を目指す生徒たちは、高校に入学すると大手予備校の模試を受験する。1,2年生の内で最もメジャーなのが進研模試で、受験者は総数40万人程度である。センター試験の受験者数約60万人と比べると、3分の2の受験生が受験する模試であり、そこから得られるデータはかなりの信憑性があると言える。
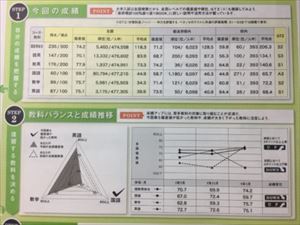
大学受験は、この60万人との競争であり、進研模試は、その競争の途中経過を我々教師側に伝えてくれる貴重な情報源である。
この情報のおかげて、過去の学生たちとの経年比較や他校の学生たちとの学校間比較など、多岐にわたる評価を教師側が行えるようになった。
これによって学生たちだけではなく、学校間もしくは教師間での競争意識に拍車がかかるようになった。進学校の教師の使命は生徒たちの進路実現、つまり、より良い志望大学に生徒たちを合格させることである。そして、多くの生徒たちの3年間の学校生活を見届けている教師は、過去の教訓を参考に、生徒たちを志望校合格のための(独自の)最短ルートへと導こうと必死になる。
この思いそのものには問題はない。問題なのは、最短ルートへ導くための手段である。生徒たちの志望校への合格確率を高めるためには、早い段階で基礎学力を定着させることが重要だと判断する。
そして、模試の時期が近付いてくると、宿題もしくは模試本番の参考として、模試の過去問を配布するなどして学生たちに普段よりも一層の学習を促すことが往々にしてある。
(注釈)この手の行動には、模試において、ある一定の成績(偏差値)を残さないいけないという周囲(の教員)からのプレッシャーによるものであったりするが、そういった要素はここでは省いて議論する。
このようにして、過去の模試の形式に慣れさせておくと、本番の試験において学生たちは良い結果を残しやすくなり、結果に満足した学生や教師たちの学習に対するモチベーションは一層高まっていくものと思われる。
しかし、ここには大きく2つの落とし穴が隠されている。
まず、1つ目が
模試の結果(順位)が自分の学力を示していると勘違いしてしまう
ことである。
高校1、2年生の場合だと、多くの学生がクラブ活動を行っていることもあり、受験に対する意識はそれほど高くない。そのような状況下において、他の学生よりも学習量で上回って得られた結果には、実際それ程の価値はない。従って、過去問の配布などを行い学生たちに学習を強いてきた学校は、大抵、3年生になると成績が伸び悩む。さらにひどい場合には、伸び悩みを挽回しようと、教師たちはさらに課題の量を増やすなどして、学生たちを混乱させてしまう。
高校1年生、2年生であれば、同じ順位・成績であっても、家庭での平均学習時間が1日4時間の学生と1日2時間の学生を比べた場合、後者の方が後半での伸びしろに期待できるが、学校ないし教師は、そこまでの分析には通常立ち入らない。
そして、2つ目の落とし穴が
本質的な問題解決スキルを学習する機会を多くの学生から奪い、論理的思考力の育成とはかけ離れた誤った学習習慣を定着させてしまう
ことである。
高校1年生、2年生の段階で受験する模試の内容は、基本レベルの問題が占める割合は高く、知識の暗記や数値計算をこなすだけで高得点がとれてしまう。
この結果、学生たちは大学入試問題でさえ、ただ盲目的に知識を暗記し、覚えた公式に数値を与えるだけでクリアできると思い込んでしまうのである。
実際、この程度のアプローチでも、かつての私と同様に地方国公立大学など、それなりに名の知れた大学に合格することは、可能である。
しかし、結果として、社会で最も必要とされる、問題の本質を明確にし、解消すべき問題点を抽出し、優先順位の高いものから順に解決に向けて着手する力のない学生たちを社会に送り出すことになってしまうのである。
そして、このような学習習慣が定着してしまった学生たちは、軒並み物理に対して苦手意識を抱く。
何故なら、物理の問題を解くということは、現実世界の複雑な状況の中から、解くことができる物理の問題を抽出することから始まるのであり、
蓄えてきた知識や数式を当てはめることではない のだから。















