
はじめに
前回の講義編に続いて、今回は問題を解いていきます。
■前回の記事
基本問題解説
(1)解説
傾斜角 q のなめらかな斜面上に質量mの物体を置き、斜面に沿って上向きに大きさFの力で距離Lだけ引き上げる。この間に力Fがした仕事を求めよ。
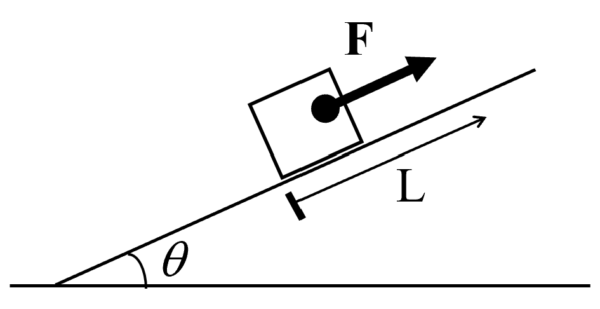
斜面に沿って、大きさFの力で距離Lだけ引き上げたので、仕事の定義より、力Fがした仕事をW1とすると、
W1=FL(答)
となります。
(2)解説
(1)のとき、重力がした仕事を求めよ。ただし、重力加速度をgとする。
質量mの物体が斜面に沿って移動することについては、重力の斜面方向の成分mgsinqが関与しています。
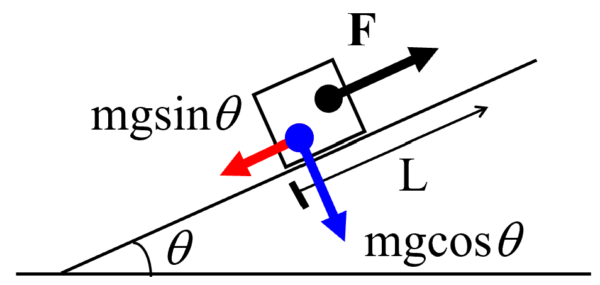
したがって重力がした仕事をW2とすると、mgsinqは、物体が移動する方向とは逆向きに作用していることに注意すると、W2=-mgLsinq となります。

この問題において重力は、物体が移動するのを邪魔していると解釈できます。
ちなみに、重力の斜面に垂直な方向成分mgcosqは、物体の進行方向に対して垂直にはたらく力なので、L移動させるという仕事には貢献していません。
したがって、重力の斜面に垂直な方向成分がした仕事は0になります。

それでは、次の問題に移ります。
(3)解説
速さv0で運動していた質量mの物体が、粗い水平面上を距離 l だけ滑ったとき、速さがv となった。このとき、物体にはたらいた摩擦力がした仕事を求めよ。
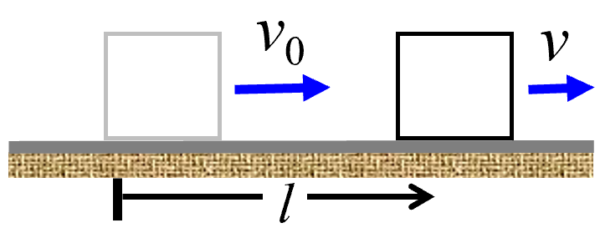
物体の進行方向にはたらく力は摩擦力だけです。
(摩擦力をFとします。)
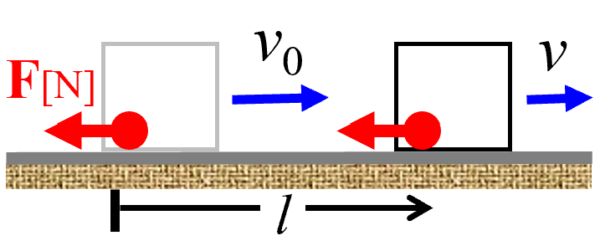

この問題では、摩擦力がした仕事を求めないといけない訳ですが、問題文には摩擦力が与えられていないので、仕事の定義W=Fxから直接求めることが出来ません。
そこで、物体の運動状態に着目をします。
それから、運動エネルギーの変化量を導いた後に運動エネルギーと仕事の関係から、仕事を求める方針で考えてみます。

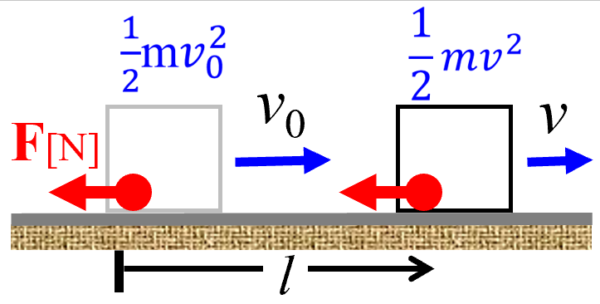
したがって運動エネルギーの変化量は1/2mv2-1/2mv02となり、これが摩擦力のした仕事に等しくなるわけですから、1/2mv2-1/2mv02 がそのまま(3)の答えとなります。

(4)解説
(3)の摩擦力の大きさを求めよ。
(3)で摩擦力がした仕事が求まりました。

摩擦力の大きさをFとすると、物体の進行を妨げた結果、物体の運動エネルギーが変化したわけです。
物体がlだけ移動したときの仕事と運動エネルギーの関係式は、1/2mv2-1/2mv02=-Fl となります。
これよりFを求めると、次のようになります。

(5)解説
(3)で、この後物体が静止するまでに移動する距離を求めよ。

物体が静止したということは、運動能力がなくなった。つまり、運動エネルギーが0になった訳です。
この時、物体が静止するまでに移動した距離をLとすると、仕事と運動エネルギーの関係式は、0-1/2mv02=-Fl となります。
(4)で求めたFを代入して、Lを求めると、最終的に次のようになります。

問題の解説は以上となります。

今回の授業では、一定の力で物体を移動させたときの仕事をW=Fxと定義して、物体を移動させることに対して、費やした労力のようなものを表現しました。
物体に力を加えると、運動状態は変化します。
そこで、一定の力から一定の加速度に着目して、運動方程式と等加速度運動の式から、物体の運動状態と仕事との因果関係を見出していきました。

それが運動エネルギーと仕事の関係です。
これらの計算過程において運動エネルギーを1/2mv2と定めて、物体の運動能力を定義しました。
次回の授業では、位置エネルギーと力学的エネルギーの保存則について学習します。そこでは、仕事とエネルギーの定義と仕事と運動エネルギーの関係が重要になってきますので、今回学んだ内容をしっかりと定着させていってください。
それでは、今日の授業はこれで終了となります。お疲れ様でした。















