目次
はじめに
力学的エネルギー保存則と一緒に、もう1つだけ見ておきたいことがあります。

それが、仕事の原理です。
エネルギー保存則というものを導くにあたって、仕事というものを間に入れて考えてきました。
□参考記事
しかし、仕事というものが曖昧であったり、決め方とか状況とかによって違うということが起きると、いつもこのように書けるとは限らないということになってしまいます。

それじゃ困るんです。
□動画による解説はこちら↓↓↓
それはどういうことかと言うと…
例えば、斜面があって最初v0だった。その後でvになったとします。
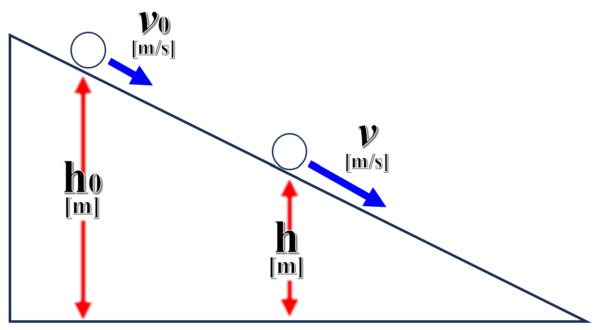

それで、最初の高さはh0です。
その後は、hです。

これのエネルギー保存則どうなるんですか。

それは、さっきと一緒です。
最初の運動エネルギー1/2mv02です。位置エネルギーはmgh0です。
後の運動エネルギーは、1/2mv2です。位置エネルギーはmghです。

これでも成り立つんです。
全く同じ式が…
しかし、このとき

なんか変じゃない?
っていう疑問を持つ人が結構出てくるんです。

だから、このことについて少し考えておきたいんです。
このことを、ちょっと頭に入れておいてください。
仕事の原理
今から仕事の原理について考えていきます。

仕事の原理っていうのは、話としてはすごく簡単なんです。
例えば、角度θの三角形の山があるんです。
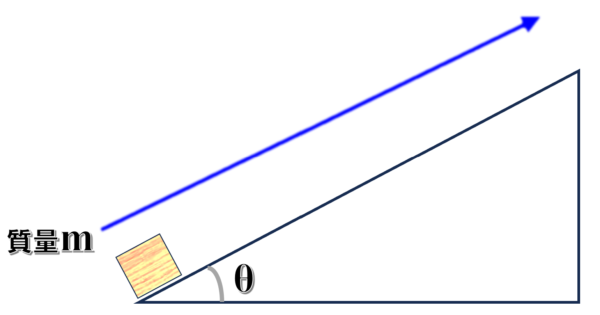
今、この床面上に、質量mの荷物があるとします。
斜面に沿って荷物を運ぶ場合

この荷物を、斜面の頂上まで持っていきたいんです。
そうすると、mgsinθという力…

摩擦は関係ないとします。
滑らかな面だと思ってください。
mgsinθと同じだけの外力を加えて、これだけ持ち上げなくてはいけません。

しかし、床面から斜面の頂上まで物体を持ち上げるには、もう一つの方法があります。
それがこれです。

mgに逆らって同じ大きさのFという力を加えて、これだけ持ち上げるという方法です。
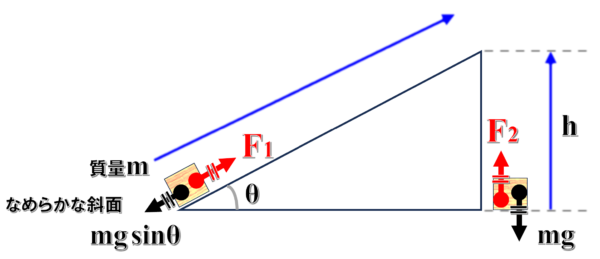
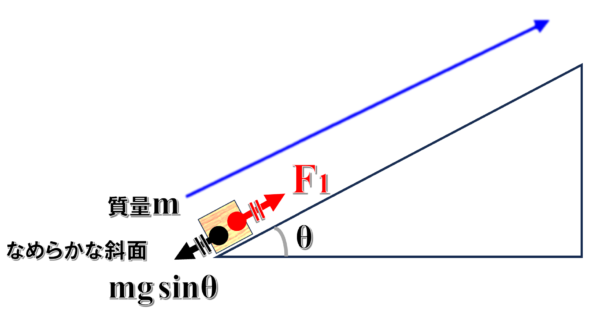
斜面上での外力をF1として、垂直に持ち上げる時の外力をF2としておきます。
さらに高さをhとおきます。

そうすると、高さがhということはこの距離はいくらになりますか??
sinθ分のhとなります。
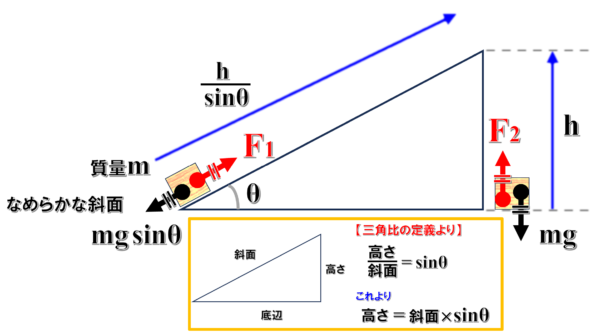
この斜面のサイン成分が高さ(=h)ですから、sinθ分のhにsinθをかけたらにhならないといけません。
F1が斜面上での外力です。ここ(斜面上)の仕事を考えると、F1という力を加えながら斜面に沿ってsinθ分のhだけ持ち上げます。

仕事は、力かける移動距離です。
しかし、F1はmgsinθです。
外力は、mgsinθなんです。
mgsinθ×sinθ分のh…

なんだ…
mghか…

荷物をまっすぐに持ち上げる場合
それでは、次に行きます。

F2の方を見ていきます。
F2という力でhだけ持ち上げます。

でもF2はmgに等しいんです。
だから・・・

mgh・・・
同じ結果になりました。
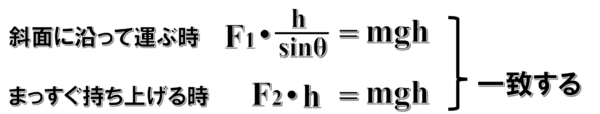

これを仕事の原理っていうんです。
どっちの道を通っていっても一緒なんです。
もともと床にあったものを上へあげたんです。

摩擦がないという条件付きですが、どこを通っても変わらないです。
これを仕事の原理と言います。
仕事の原理について
要は、高さhっていうところに上げるのに、いっぺんに上げるのは大変です。

だから、斜面を利用したり、動滑車なんかの道具を利用して、よいしょよいしょよいしょって上げたら力は楽になるかもしれない・・・

けど距離が長いんです。
これを仕事の原理っていうんです。

どんなに道具を使っても、得しないんです。
例えば、すごい重たい石があるんです。

これをてこを利用して、何とかぐっと持ち上げようとしてる訳です。

てこを利用して持ち上げようっていうときに、こんなところに石は置かないですよね。

これじゃあ、しんどくて上がんないです。

だからこんなところにはてこを置かないで岩の近くに置きます。
そうすると楽になります。

てこは力については弱くていいんですが、距離は長いんです。
こんなにもやったのに、これだけしか上がらないんです。

これと一緒なんです。
こんな経験はないですか??

みんなの自転車に変速ギアは付いてないですか??
その中にスピードが速くなるギヤがあります。

でも、それで自転車を漕ぐと、とても重たいです。


坂道とかになったら、ガチャガチャガチャって、すごく力が軽くなるギアに変えます。

でも、一生懸命、漕いでるわりにはたいして上がらないですよね。
一緒なんです。
仕事は…。
こういうのを仕事の原理といいます。

だから、さっきも言ったように真っすぐの所でv0,vってやろうが、
斜面でv0,vってやろうが、エネルギーを考えるときは関係ないんです。

とても便利です。
だから仕事の原理について、少し説明をしました。
どんなに道具を使っても、トータルすると得してないんです。

斜面とかを利用したり、滑車とかテコとか、道具を使うっていうのは、
その場での力は楽だと言ってるだけです。
その場での力は楽なんです。

動滑車を使えば力は半分で済みますが、距離は2倍必要になるからトータルでの仕事はかわりません。
例題解説
それでは、例題の方に移っていきます。
例題1解説
小球がなめらかな斜面上の高さ0.10mの点から静かにすべり下り、なめらかな水平面上に達してからは等速直線運動をした。このときの小球の速さは何m/sか。重力加速度の大きさを9.8m/s2とする。
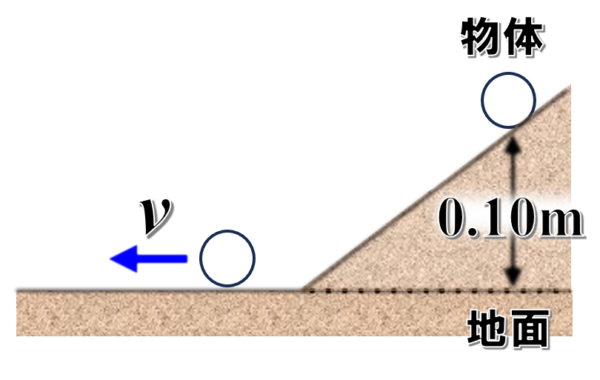
【例題1】
今から、この問題を力学的エネルギー保存則で解いていきます。
小球の質量はm、求める小球の速さをvとします。

最初、小球は静かにすべり降りたわけですから最初の速度は0と考えます。
したがって、運動エネルギーは、1/2×m×02で0
重力による位置エネルギーは質量m×重力加速度9.8×高さは0.10 となります。
そして、滑らかな面に到達した後の力学的エネルギーは、運動エネルギーが1/2mv2
重力による位置エネルギーは、質量m×重力加速度9.8×…
(小球は基準水平面にあるから)高さは0
したがって、0です。
よって、力学的エネルギー保存則より、
この両辺は等しいとして、vを求めると、
両辺をmで割ってmを消去して、
v2の式にすると1.96。1.96は1.4の2乗ですから、
速さ、vは1.4m/sとなります。
vの2乗の平方根なので、本来はプラスマイナスでvは出てきますが、ここでは問題文の状況より
vは正の数であるという前提で解答しているので注意してください。


これで解答は、終わりましたが、次の問題に移る前に1つ疑問が残ります。
なぜ力学的エネルギー保存則なのか??
定期考査では範囲は決まっているから、

あぁ、ここでは力学的エネルギー保存則だ!
ってわかりますが、

模擬試験や入試本番では範囲が決まっていません。

速さを求めたい。
じゃあ、等加速度運動の式だ
と言っても、この問題は解けません。

それなら運動方程式を立てて加速度を求めてから・・・
とやってもダメです。

だから、問題を解くためには理由が必要になってきます。
なぜ力学的エネルギー保存則なのか??
これは、すぐに分かります。
最初、小球は止まっていたんです。
それが水平面では動いてるんです。
運動能力を持っているんです。

誰のせいですか?

重力のせいです。

重力が何をしたんですか?

高さ0.10mだけ働いたんです。

力Fが距離xだけ働いた。
ここでは、力mgsinθが距離sinθ/x 動いたから、最初、止まっていたものが動き出したわけですが…

仕事の原理によると、「力Fが距離xだけ働いた。」と考えても良いわけです。
それなら、力と距離の関係です。
仕事からエネルギーです。
したがって、別解として仕事と運動エネルギーの関係より、最初止まっていたものが、速度vで動きました。それは、仕事によってもたらされた。

という式が出来ます。
これを解いても、vは1.4m/sという結果が出てきます。

こうして2つの解法を並べてみると、エネルギー保存則を理解するためには、「仕事とエネルギーの関係を理解する」ってことがいかに大切かわかってもらえると思います。
例題2解説
それでは次の問題に移ります。
ばね定数25N/mのばねをなめらかな水平面上に置き、その一端を壁に固定する。ばねの他端に質量0.16kgの小球を押しつけ、ばねを自然の長さから0.20mだけ縮めた位置で静かにはなした。ばねが自然の長さになった位置で小球はばねから離れた。ばねから離れた後の小球の速さは何m/sか。
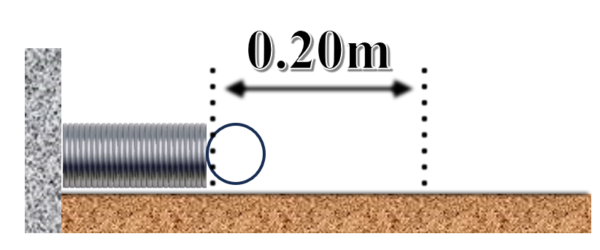
まずは、力学的エネルギー保存則を使って解いていきます。
求める速さをv とすると、運動エネルギーは、最初は止まっているから0
弾性力による位置エネルギーは、1/2kx2なので、1/2×25×0.202
重力による位置エネルギーは初めと終わりで基準点が変っていないので、数式には含めないことにします。
敢えて書くのであれば、地面を基準水平面としたときにmghですから、高さは0ということで
重力による位置エネルギーも0です。
そして、後の力学的エネルギーは、
運動エネルギーは、1/2×0.16×v2
弾性力による位置エネルギーは、1/2×25×02で0
したがって、この式よりvを求めると、次のような計算過程を経て、2.5m/sとなります。

この問題についても、先ほどの例題と同じように仕事とエネルギーの関係から求めることが出来ます。

最初止まっていた物体が速度vで運動するようになったのは何故か?

それは、ばねが物体に仕事をしたからです。

ばねがした仕事は、弾性力による位置エネルギーを考える時にグラフを用いて考えました。
今回もグラフの三角形の面積を考えるとばねがした仕事を求められますが、今回は弾性力が最も大きな状態から0になるまでの仕事ですから、前回とはグラフの形が少し違うので注意しましょう。

しかし、面積は変わらず1/2Fxで、フックの法則よりF=kxですから、1/2kx2
したがって、仕事とエネルギーの関係式は、次のようになります。


「最初止まっていたものが、速度vで運動するようになったのは、小球がこれだけの仕事をされたからだ!」という式になります。
これを解いてもvは2.5m/sとなります。

どちらの解き方でも大丈夫ですが、どちらの考え方でも解けるようになっておいた方がいいです。
それでは今回の解説は以上となります。