はじめに

それでは前回に引き続き問題の解説を行います。

□前回の記事

 

今回は、仕事とエネルギーの関係性にまつわる問題を中心に進めていきます。

 

仕事とエネルギーの関係

 

仕事とは「力かける距離」で定義される物理量で、物体に対して与えた労力のようなものです。

 

一方、エネルギーとは、仕事をする能力を指します。

 

これから、仕事とエネルギーの関係を見ていくわけですが、
エネルギーには、運動エネルギーと位置エネルギーがあることを学習しました。

 

運動エネルギーについて

 

例えば、運動エネルギーというのは、加速度aで等加速度運動している物体が、初速度v₀で動いていたとします。

 

 

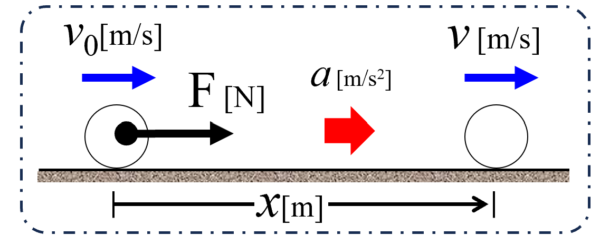
距離ｘ移動したときに速度がｖに変化したとすると、等加速度運動の式によって、v²－v₀²=２axと
表すことができます。

 

この式の両辺にｍをかけて、さらに2分の１をかけると右辺は仕事Fxという表記に変化します。

 

 

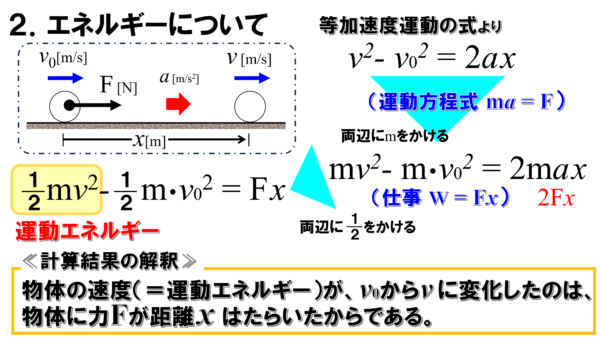
そこで左辺の1/2mv²という表記に対して、運動エネルギーという名称を与えることで、

 

 

　物体の運動能力が変化したのは、物体が仕事をされたからである。

 

という風に、

 

 

ということでした。

 

位置エネルギーについて

 

一方、位置エネルギーについては、重力によるものとばねの弾性力によるものを考えました。

 

重力による位置エネルギーについては、

 

　物体をｍｇに逆らって、ｈ持ち上げるという仕事をすると、Ｕ＝ｍｇｈという落下能力を持った！！

 

ｍｇｈという仕事をしたから、それだけ下に落ちる能力を獲得した。

 

 

そして、弾性力についてはグラフを用いて、ばねに対してした仕事を求めてから、最終的にばねの弾性エネルギーは1/2kx²であるということを見ていきました。

 

 

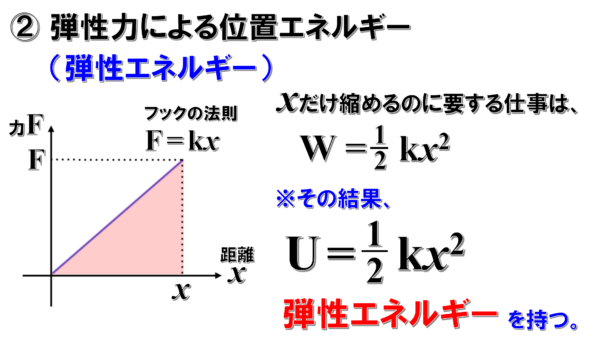
そのようなことを踏まえながら、これから実際に問題を解いていきます。

 

問題解説

 

問題６

 

手によってなされた仕事を求める問題ですが、手が加えた力の大きさがわからないので、質量ｍの物体にはたらく力をまず整理します。

 

 

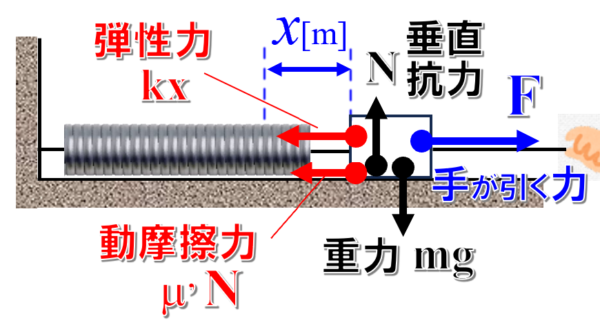
すると、物体には、重力と垂直抗力。摩擦力と弾性力。

そして、手が引く力の５つの力があることがわかります。

 

 

 

この内、問題文に与えられているのは、ｍ, ｋ, ｘ, μ’ g だけですので、それ以外の数値については、問題を解きながら考えていきます。

 

問題文にある通り、

 

　この物体をゆっくりと引き伸ばす…

 

とあるので、進行方向の力のつり合いを保ったまま引き伸ばすと考えると…

 

　手が引く力の大きさは、摩擦力と弾性力の大きさに等しい

 

と、できます。

 

したがって…

 

 

としてしまいがちなのですが、それは誤りなので注意してください。

 

 

 

 

 

ここでのＦは、ｋｘ＋μ’ｍｇ です。

 

動摩擦係数と重力は一定の値だから、μ’ｍｇは一定ですが、ばねの弾性力ｋｘは、ばねが伸びれば伸びるほど、力は大きくなります。

 

 

 

したがって、W=Fx ではＷは求められません。

 

そこで、仕事とエネルギーの関係でやったことを思い出してみます。

 

ばねの弾性力による位置エネルギーを求めるために、グラフを書いて、面積分に相当する仕事がばねにはたらいたから、その結果、ばねは弾性エネルギーを持った。

このようなことをやりました。

 

ここでも同じ事をやってみます。

 

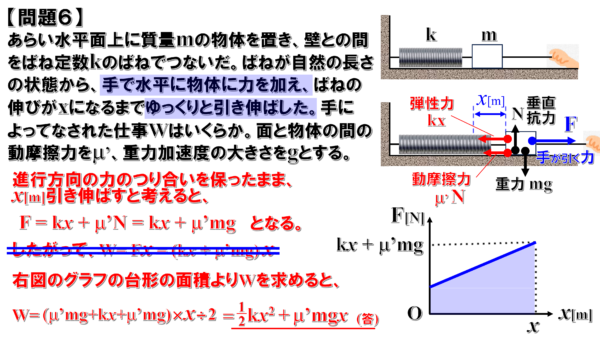
物体を、ｋｘ＋μ’ｍｇという力でゆっくりとｘだけ引っ張りました。

 

すると、こんなグラフになります。

 

 

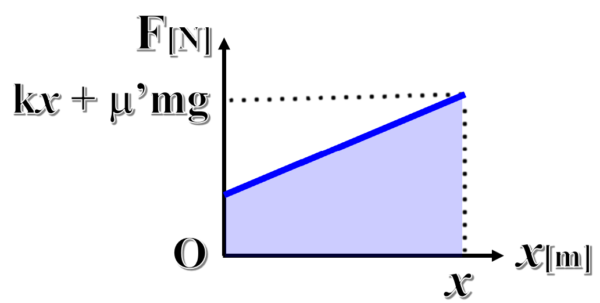
最初ばねは自然長だったから、弾性力は０。

したがって、Ｆはμ’ｍｇから始まって、ｘ伸びたところでｋｘ＋μ’ｍｇという力になった。

 

このグラフの面積を求めると、台形の面積は上底＋下底×高さ÷２ですから…

 

仕事Ｗは、1/2kx² ＋μ’ｍｇx となります。

 

問題７

 

これは、仕事と運動エネルギーの関係をそのまま問う問題です。

 

 

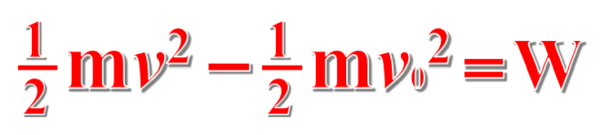
この時の速さｖは、ｖ＝…の式に変形すると、次のようになります。

 

 

 

 

 

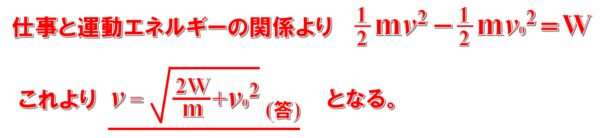
問題８

 

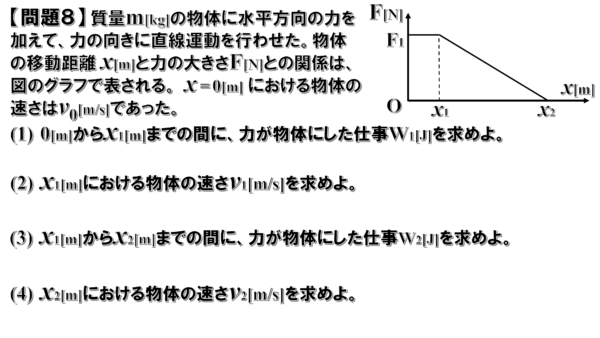
（１）解説

 

こちらは、問題６と同じ考え方で行きます。

 

 

したがって、０ｍからx₁[m]までの仕事、W₁はF₁x₁となります。

 

（２）解説

 

これは問題７と同じように考えていきます。

仕事と運動エネルギーの関係より、0[m]からx₁[m]までの間に物体はW1の仕事を受けた結果、運動エネルギーが1/2mv₀²から、1/2mv₁²に変化します。

 

 

次の式より、v₁を計算すると、次のようになります。

 

（３）解説

 

こちらもグラフの面積を求めるだけです。

 

 

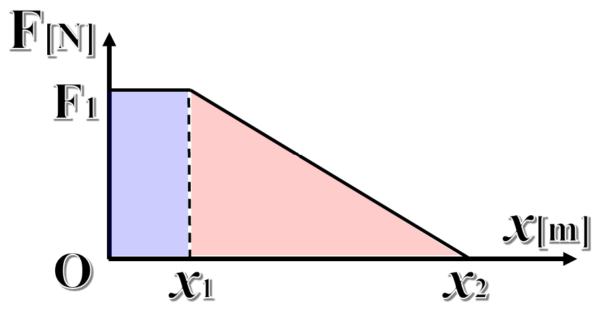
そうすると、x₁からx₂までは、この三角形の面積（上図赤色部分）を求めたらいいので、

 

W₂＝1/2F₁(x₂-x₁)[J]となります。

 

（４）解説

 

（２）の問題と同じように、仕事と運動エネルギーの関係を考えると、

　x₁[m]からx₂[m]までの間に物体はＷ_２の仕事を受けた結果、運動エネルギーが1/2mv₁²から、1/2mv₂²に変化した。

ということで、このような式になります。

 

 

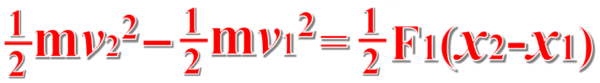
これよりv₂を求めると、次のようになります。

 

 

 

 

 

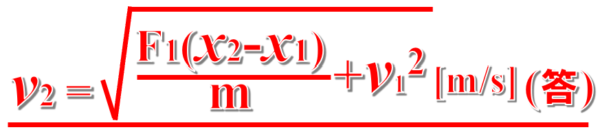
それでは最後の問題です。

 

問題９

 

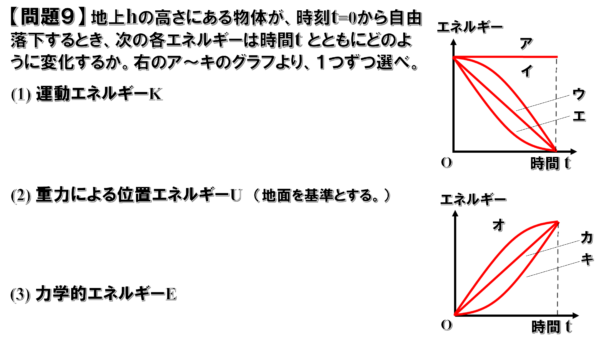
（１）解説

（１）番から順番にみていきます。

まずは、運動エネルギーです。

 

 

そして、今回は物体が自由落下するわけですから最初の速度は０です。

 

そして、重力加速度をｇとすると、ある時刻ｔでの速度ｖは等加速度運動の式よりｖ＝ｇｔと書けます。

 

これをＫ＝1/2mv²の式に代入すると、Ｋ＝1/2mg²t²とかけるので、運動エネルギーＫは時間tの2次関数の式になっています。

 

この式は下に凸な概形をしたグラフでｔ＝０のときＫ＝０ですから、ア～エは、まず選択肢から外れます。

 

残りのオ～キの中で最適なグラフを選ぶと、キが運動エネルギーＫのグラフということになります。

 

（２）解説

 

次に、(2)番、 重力による位置エネルギーUです。

Uは、地面を基準とした時、「重力×基準点からの高さ」で表現される物理量ですから、

 

最初ｔ＝０の時には高さｈの地点にいたとすると、この時の位置エネルギーはｍｇｈです。

そして、自由落下することによって、どんどん高さが０になっていくわけですが、ある時刻ｔにおける変位（位置の変化量）は、－1/2gt² と書けます。

 

時刻ｔにおける高さをｙとすると、ｙ＝h-1/2gt² と書けます。

 

したがって、ある時刻ｔにおける位置エネルギーを、重力ｍｇ×基準点からの高さｙで表すと、

Ｕ＝ｍｇ×(ｈ－1/2gt²) と書けます。

 

この式より、重力による位置エネルギーＵは、ｔの2次関数であることがわかります。

 

ただし、今回は上に凸なグラフの概形になります。
従って、最適なグラフはイかオのいずれかになります。

 

そして、この式はｔ＝０の時に最大値となるグラフなので、イが重力による位置エネルギーＵのグラフとなります。

 

（３）解説

 

そして、最後に力学的エネルギーＥです。

 

 

つまり、Ｅ＝Ｋ＋Ｕ　で表される物理量です。

 

そこで、（１）番、（２）番で求めたＫとＵを代入すると、

 

Ｅ＝ｍｇｈとなります。

 

この式をよく見ると、ｍは定数、ｇは重力加速度9.8、つまり定数。ｈは最初の高さで定数。

 

 

 

Ｅの式には変数が含まれていないので、どんな時間であってもＥはｍｇｈです。

 

したがって、ア～キより最適なグラフを選択すると、アということになります。

 

 

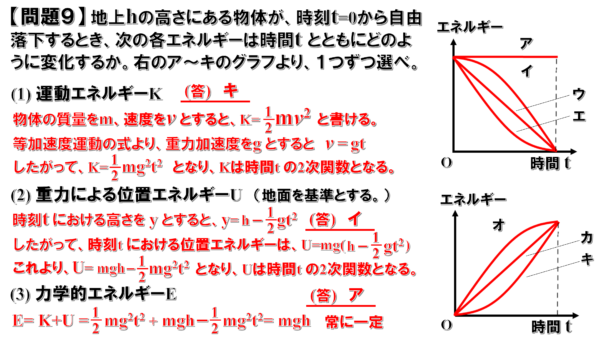
Ｅが一定の値になることを力学的エネルギーが保存されると言いますが、この辺りの問題については、次回の問題解説で行う予定です。

 

それでは今回は以上となります。