はじめに
今度は、両端が自由。この場合について扱っていきます。

両端が自由…

そのような弦はありません。

それは、そうです。

弦は両端を固定するから弾くことができるんです。

両端を自由にしたら…

弦というよりは、その辺に捨ててある糸くずと一緒です。


そんなものを弾いても何も起きません。
だから、この先は、弦に変わって気柱について考えていきます。
気柱について
そこで、今回はまず両端が空いている気柱から考えていきます。
たとえば、ストロー…

あれも気柱の1つです。
水道管の両側をバンバンと切ってしまえば気柱になります。

両端が開いています。

ですから、うまく吹くと音が出ます。
小学校の時につかった笛の裏側を見てください。


穴が空います。
ランドセルの横に笛を立てて通学したことがあると思います。

私が小学生の頃は、笛を吹きながら通学する生徒もいました。
今日、音楽の試験だからと言って、穴を塞いだりすると、ドレミファソラシドって音が変わりました。

このように、穴を開けたりして気柱の長さを変えているんです。
気柱の長さが変わると、節ができる場所とか、腹ができる場所が変わります。

音が変わるんです。

だんだんイメージ出来てきたでしょうか…??
子供の頃は、笛をいかに上手に吹くかということで、一所懸命、穴の押さえる位置とかを覚えていたかもしれませんが…

これからは、「なんでそういうことをすると、音が変わるのか!?」
ということがわからないといけません。
皆さんからすると、

今更笛の原理が分かったからって、
なんなんだ!
と思うかもしれません。
ギターの弦を弾いて、

どんな波ができた…??
と聞かれても

そんなこと知るか!?
って思われるかもしれません。

しかし、よく考えてください。
例えば、建築家になりたいなと思ってる人…

そんな人が将来、大きなビルを建てる仕事に関わるとします。
その中には、空調システムを導入しないといけません。


天井裏に大きなダクトをつけて、部屋と部屋を結んでいって、エアコンとつながないといけません。


その時です。
使用している部屋は、エアコンのスイッチが入っている間は、蓋が空いてます。

エアコンを使用していない部屋は閉まっています。

そして、屋根裏のダクトの中を空気がバァ~っと流れていきます。


これって大きな笛じゃないですか。
ビルの天井裏は、いわば大きな笛で、スイッチが入ったところは、ぴっと空いているんです。
スイッチが切れたところは、パッと閉じてあります。
大きな笛です。
その時に、

はい。ビルが完成しました。

「さぁ、空調を付けてみましょう!」って、ピッと空調をつけた瞬間、ブわ~って音がしたらどうするんですか?
それでは使い物になりません。

定在波ができたらいけないんです。
ですから、私たちは、笛を作るためだけに、こういうことを一生懸命勉強してるわけではないんです。

じゃあ、弦はどうなんですか?

その辺を見てください。
吊り橋を見たことがあると思います。


大きな吊り橋…、
高速道路とかもそうです。

あれは、1個、1個、長い鉄骨をつないでいるわけです。
あの1つ1つが弦なんです。

そんな道路にもしも定在波がバァ~っと、できたらどうですか?
【参考】タコマ橋(米国)崩落映像(「振動の世界」より)

ものすごく振動するところと全く振動しないところが交互に並んでるんですか?

そんなことをしたら、道路がすぐにブチ切れてしまいますよ。

それは、とんでもないです。
だから、こういうものを作る時は、絶対に定在波ができないように設計してあります。

たとえ、ゴールデンウィークで大渋滞していても、平日の昼間にがら空きになっていようと、絶対に定在波が出来ないように作ってあるんです。

だから安心して渡れるんです。
今は、とても大事なことをやっているんです。
ただ身近なものとして笛とか弦を例に出してるだけなんです。
気柱の共鳴(両端が自由端)
すこし話が脱線しましたので、そろそろ本題に行きます。

両端が空いてるんです…
ということは両端が自由に動けるわけですから、今度は両端を自由に動けるようにしてあげてください。
だから波長が最も大きい時はこうなります。

この長さをl とした時、1波長は、山から山までの距離ということで、
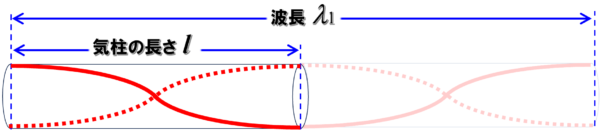
気柱の端から端までは、λ1/2
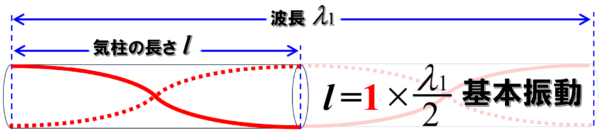
前回の弦の場合と同じです。

そして、前回同様、赤で書かれた1が大事なんです。
両方空いているのがワンセットという、この形が基本になります。
この「蝶ネクタイのマーク!」

これが何個あるかで決まる訳です。
だから、蝶ネクタイが2個あれば2倍し、

3個あれば3倍します。
したがって、2倍振動、これが3倍振動、

そして、m倍振動はこのようになってくる訳です。
気柱の共鳴(一方が固定端、他方が自由端)
では最後に行きます。
両方が固定、両方が自由の場合をやりましたから、今度は一方が固定。他方が自由という場合です。

これは、具体的に、どんな場合が考えられると思いますか??
一方が固定されていて、他方が自由になっている。

これはジュースの瓶なんかがそうです。

片方は口が空いてるけど、底は閉じています。
片方を閉じておかないと、底からジュースがもれてしまいます。
だから、一方は固定されています。
端っこに壁があるから、ここでは空気は振動できません。
だから、閉じたところでは、弦の端っこと同じく定在波の節となります。
一方、もう片方の端は自由に動けます。
したがって、こういう状況です。
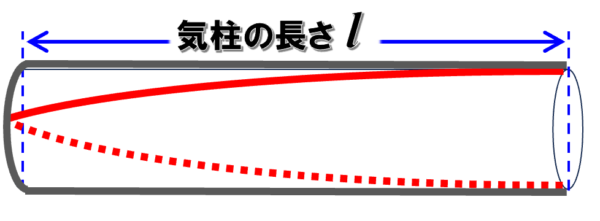

これが最大波長だったらどうなるのでしょうか…??
こんな感じになります。
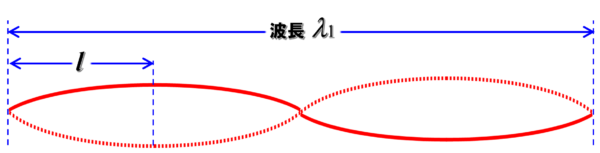
そうすると、ここの寸法をlになるから、1波長の波形と比べると、ここの寸法は、λ/4 です。
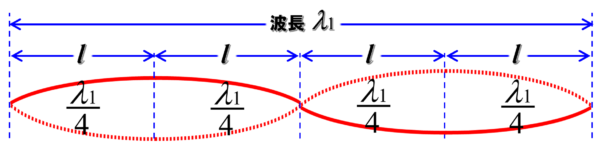
したがって、図より、lイコールλ/4 が1個。

そして、これまでと同じく、赤い字の1が大切です。
このようになります。

しかし、これで、話が終わったわけではありません。そこのところは、よく注意して見て行かないといけません。
それが何かと言うと、今、確認した波形…

これが基本振動なんです。

片方が閉じていて、片方が空いている基本的な形っていうのは、まずこの形です。
そして、「これが何個あるか?」 というのが倍振動なんです。

その考え方でいいんです。
しかし、ここから、よく考えてみてください。

例えば、2倍振動を考えてみたらどうなりますか?
2倍振動ってこれが2個あるって言うんです。

これが2個あるのか…。
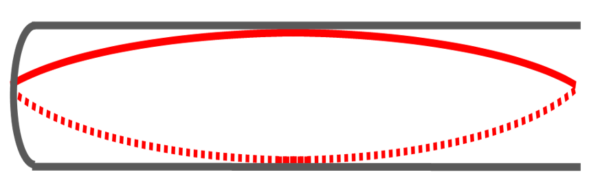

1個2個。あれ??

両端が自由になってしまった。

これでは駄目です。

じゃあ反対側をやってみます。
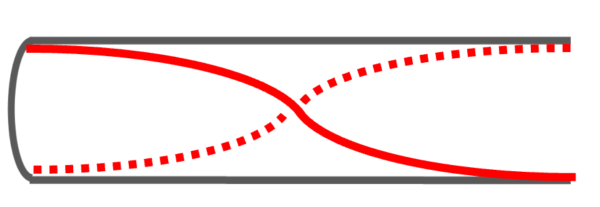

1個2個…

今度は両端が固定されてしまいました。
片方が固定で片方が自由じゃないといけません。

これはルール違反です。
だから、この場合は成り立っていないんです。
もしも、3倍振動だったらどうなるか、
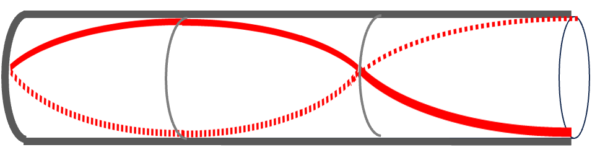

1個2個3個。片方自由で片方固定になってる。

これは、ちゃんとなってます。
つまり、これは2個集めたらいけないんです。
4個も駄目です。

もうわかってもらえますか…??
だから、3倍振動の次は5倍振動です。

覚えるんじゃないんです。基本を頭に入れておいて、その上で、「偶数個だとルール違反になってしまう。」ということが分からないといけません。
この場合だけは、奇数倍振動しか存在しません。
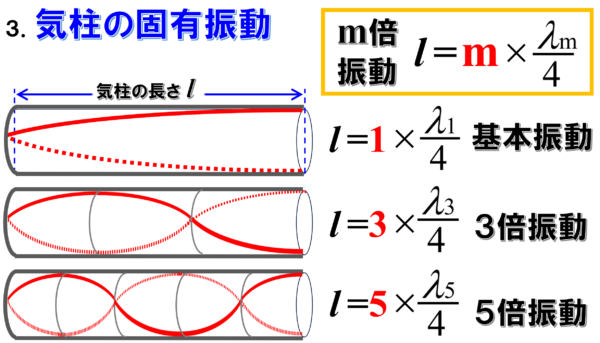
したがって、m倍振動の時のmは奇数になります。
(m=1,3,5,…)
今回の解説はここまでとします。

次回は、弦も含めて、これまで今まで勉強してきたことを、「一体どうやって問題に使っていけばいいか?」ということを例題を使いながらやっていきます。














