目次
はじめに
それでは引き続き問題の解説を行っていきます。
ここでは、力学的エネルギー保存則に関して保存力以外の力が仕事をする場合の問題を中心に取り扱っていきます。
基本事項については、前回の記事を参考にしてください。
力学的エネルギーが保存されるのは、物体にはたらく力が保存力だけであるか、保存力以外の力がはたらいていても仕事をしない場合だけでした。


高校物理で学習する保存力とは重力やばねの弾性力や静電気力、それ以外の力は保存力ではありません。
それでは、保存力ではない力…

たとえば摩擦力などが仕事をした時はどうすればいいのか!?

この場合は力学的エネルギーは保存されません。
こういったところを中心に解説していきます。
■問題解説
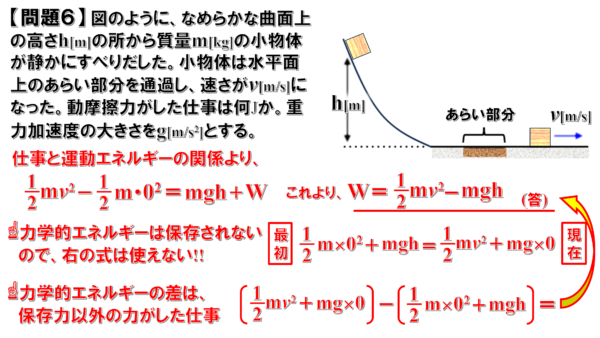
問題6
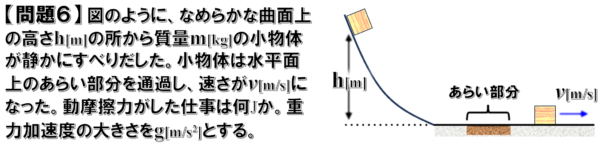
動摩擦力がした仕事を求める問題です。
仕事は力×距離ですから、物体にはたらく摩擦力を考えて移動距離さえわかれば、それで問題は解決するわけですが…

問題文には、摩擦力を求めるための動摩擦係数であったり、移動距離が与えられていません。
したがって、直接的な解法では解答に至らないので、違ったアプローチを図らないといけません。
そこで、仕事とエネルギーに着目して、問題を見ていくと…

最初、静止していた小物体がすべりだして、斜面を滑り降りてからあらい面を通過します。すると速さがvとなったと言っています。
ですので、一度、運動エネルギーと仕事の関係式を考えてみます。

そうすると、

最初止まっていたものが速度vで動くようになったのは、重力がmghだけ仕事をして動摩擦力が仕事をしたからだ…
このような式が出来ます。動摩擦力がした仕事をWとしています。
垂直抗力は、進行方向に垂直にはたらく力なので、仕事は0であることに注意してください。
この式から、動摩擦力がした仕事を求めることができます。
したがって、動摩擦力がした仕事は、次のようになります。
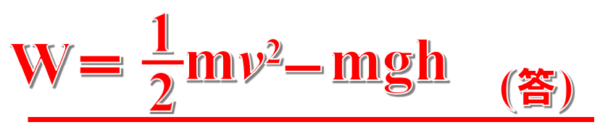

さきほども説明した通り、この問題では保存力ではない摩擦力が仕事をしているので、力学的エネルギーは保存されません。

試しに、前後の力学的エネルギーの差をとってみると次のような式になります。
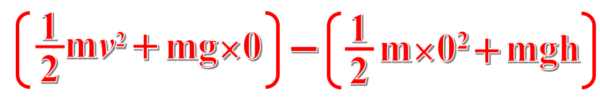
この式をよく見てもらいたいのですが、
これを計算すると 1/2mv2ーmgh となっています。
今回の問題では、このように考えても動摩擦力がした仕事が求められます。
つまり、
力学的エネルギーが変化した分が保存力以外の力がした仕事になる。
というわけです。
このようにどうして、このような式が成立するのかといったことも理解しながら進めていってください。

力学的エネルギー保存則は成立しませんが、仕事と運動エネルギーの関係式は成立します。
そして、仕事と運動エネルギーの関係式を応用すると力学的エネルギーが変化した分が保存力以外の力がした仕事になる。
こうやって考えていくこともできます。
それでは次の問題に移ります。
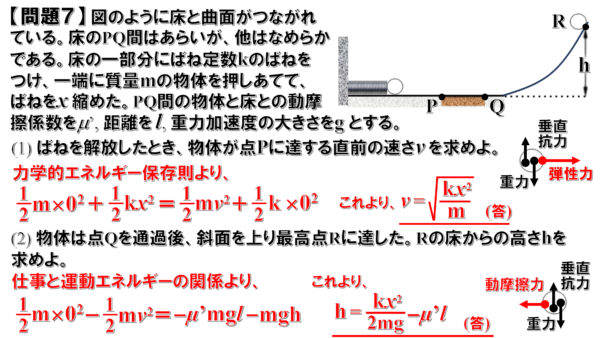
問題7
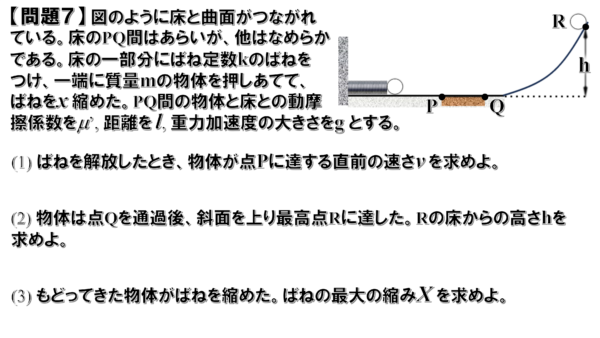
(1)解説
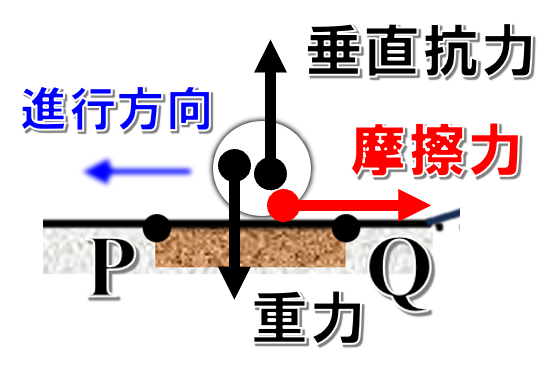
ばねを解放してから物体が点Pに達するまでは、物体にはたらく力は、重力と垂直抗力、そしてばねの弾性力です。

その内、重力と垂直抗力は進行方向に対して垂直にはたらく力なので、水平方向に移動することに関しては、仕事をしません。
そして、弾性力は保存力です。
したがって、力学的エネルギーは保存されます。
よって、ばねをx縮めて解法する時と点Pについて、次のような式が出来上がります。

これよりvを求めると、

となります。
(2)解説

PQ間では、摩擦力がはたらいているので力学的エネルギーは保存されません。
そこで、先ほどの問題と同じく、仕事と運動エネルギーの式を立ててみます。
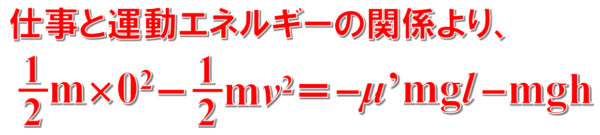
最初vで動いていた物体が点Qを通過して最高点に達して、速さが0になったのは、PQ間を通過する時に、摩擦力が仕事をして、それから、斜面を登る時に重力が仕事をしたからだ…
こんな意味の式になります。
動摩擦力がした仕事は、ーμ’mglですが、これは垂直抗力とつり合う力がmgで、それにμ’をかけて μ’mg
それがPQ間で作用するので、μ’mgl、
そして、進行方向とは反対にはたらく力なのでマイナスがついて、ーμ’mglです。
それから、重力がした仕事ですが、仕事の原理より、斜面を登っても真っすぐhだけ上昇しても
仕事量は同じなので、mgという力の逆らってhだけ上昇したと考えています。
ここでも重力は上昇する方向とは逆向きはたらいているので、マイナスがついて、ーmghとしてあります。
この式からhを求めると
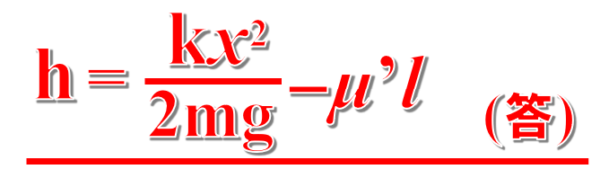
となります。
別解について
ここでは、仕事と運動エネルギーの関係から問題を解きましたが、前後の力学的エネルギーの差が動摩擦力がした仕事であるという関係から数式を考えていくと、次のようになります。
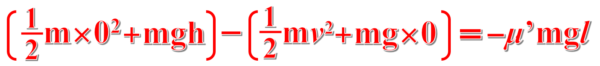
ここでのmghは重力による位置エネルギーで、先ほどのーmghは重力がした仕事として考えています。

同じ形をした文字式ですが、数式の解釈によって、意味が異なってきますので、公式に数値を代入するだけではなく、1つ1つの数値がどのような意味を持っているのかを吟味することを欠かさないようにしてください。
それでは次の問題です。
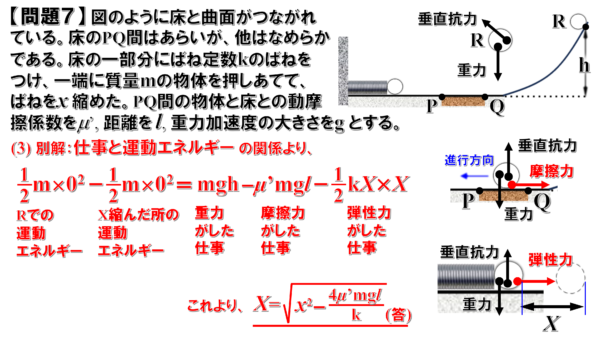
(3)解説
ここでは、最高点Rから、再びもとの場所に戻ってばねを縮めることを考えます。

ここでも、PQ間を経由するので、動摩擦力が仕事をした分だけ、前後の力学的エネルギーは変化します。
したがって、次のような式ができます。


最高点では速さは0だから運動エネルギーは0、ばねは関係ないから弾性エネルギーも0、重力による位置エネルギーはmghです。
そして、ばねをX縮めたところでは…

物体は一端静止するから速さは0で、運動エネルギーは0、基準水平面に物体はあるから重力による位置エネルギーは0、ばねはX縮んでいるから弾性エネルギーは 1/2kx2です。
それぞれの力学的エネルギーの差をとったら、動摩擦力がした仕事になるわけですから、ーμ’mgl となります。
この式から、
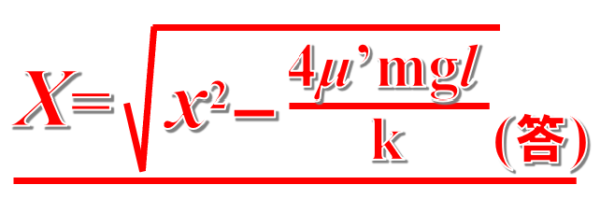
となります。
別解について
参考までに、仕事と運動エネルギーの関係から、問題を考えていくと次のようになります。

運動エネルギーは、始まりと終わりでは速さは0なので、0のまま。
つまり左辺は0になります。
最高点にある物体には、垂直抗力と重力がはたらきますが、垂直抗力は仕事をしないので0。
重力がした仕事は、仕事の原理を応用すると、mghとなります。
そしてPQ間を経過する時にはたらく力は、重力と垂直抗力と摩擦力ですが、その内、摩擦力だけが仕事をして、その仕事量はーμ’mgl
そして、物体がばねをラージX縮める時には、弾性力が作用しています。
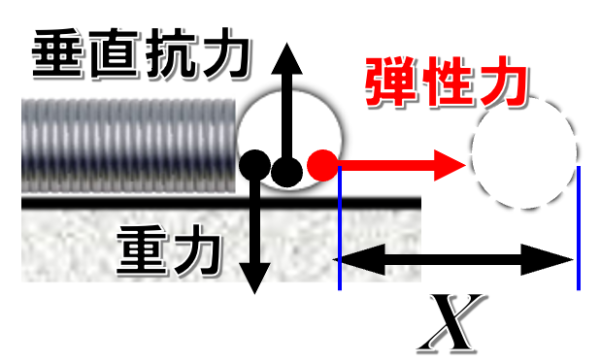
弾性力がした仕事は、ばねがだんだん縮んでいくについて、力はばね定数kに比例して上昇していくので、その仕事は、グラフを用いて考えると、2分の1kxの2乗。
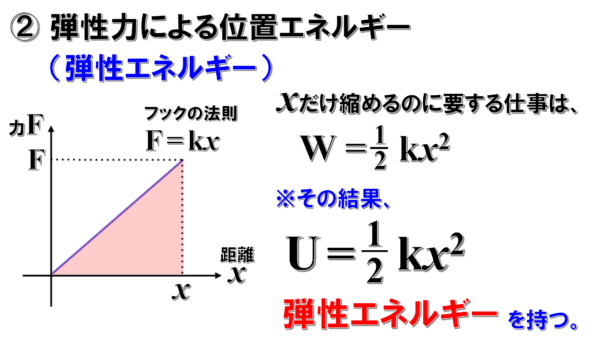
この式から、Xを求めることもできます。

定期テストで問題を解く時は、いずれかの解き方で解けば良いわけですが、いずれの考え方でも解けるようにしておいた方が物理の実力がつきます。

それでは最後の問題です。
問題8
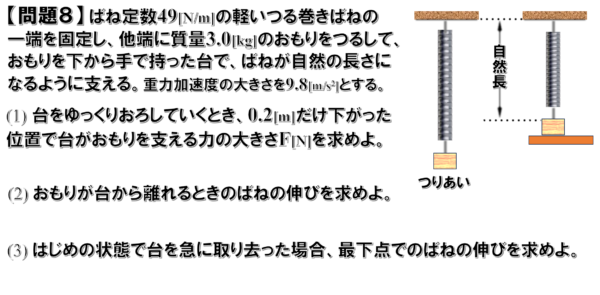
(1)解説
まずは、おもりにはたらく力から整理していきます。
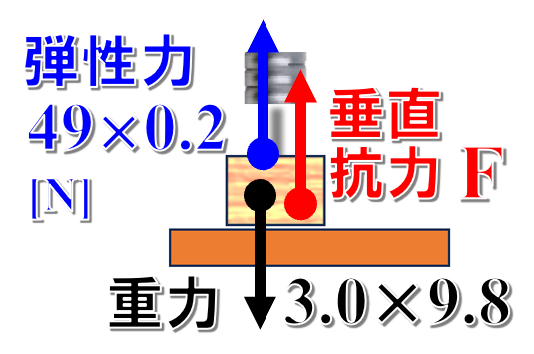
物体にはたらく力は、重力と板からの垂直抗力、そしてばねの弾性力です。
図の垂直抗力が、台がおもりを支える力の大きさFとなります。
問題文より、おもりをゆっくりとおろしていくとあるので、おもりが静止している、もしくはほぼ同じ速さでゆっくりと等速直線運動していると考えると、慣性の法則より、おもりにはたらく力はつり合っています。

したがって、力のつり合いの式は次のようになって、これよりFを求めるとFは19.6Nとなります。
(2)解説
おもりをゆっくりとおろして行って、やがて台から離れる時、おもりと台は接触しないわけですから台はおもりを支えることが出来ません。
したがって、この時、垂直抗力は0Nです。
よって、おもりにはたらく力は、重力とばねの弾性力だけであり、この時のばねの伸びをx とすると、
力のつり合いの式は次のようになります。
![]()
これよりxを求めると、xは0.6mとなります。
(3)解説
はじめの状態から急に台を取り去ると、おもりはつり合いの位置を越えて行きます。
だから、ここでは、最下点でのおもりの速度が0になると考えて、ばねの伸びを求めないといけません。

そこで、ここでは力学的エネルギー保存則を使って、問題を解いていきます。
すると、はじめの状態と最下点では次のような式が成立します。
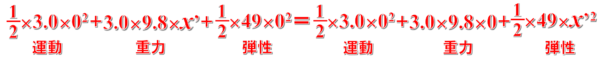
この式では、ばねの伸びをx’、最下点を基準水平面として考えているので、はじめの状態では重力による位置エネルギーは、mgx’、最下点では0となっています。
そして、ばねの弾性エネルギーは、はじめは0で最下点では1/2kx'2 です。
これより、x’を求めると、x’=1.2mとなります。
この問題は、専門物理の方で学習する内容を利用すると台を急に取り去った後のおもりは単振動すると考え、振動の中心が力のつり合いの位置であることが分かれば、最下点でのばねの伸びは、(2)の2倍になることがわかります。
これよりx’は1.2mであるとすることもできます。
ちなみに、(2)と(3)の違いですが…
(3)ではおもりにはたらく力は、重力と弾性力だけなので、力学的エネルギー保存則は保存されますが、
(2)のように、台をゆっくり下ろしていく場合は、おもりを支える力によって負の仕事をされ、力学的エネルギーが減少していくので、つり合いの位置でのおもりは静止します。
このような運動の違いが生じています。
それでは、今回の解説は以上となります。

















