3.はねかえり係数(反発係数)
ここでは、はねかえり係数について確認します。
衝突について、もう一つだけ伝えておかなければならないことがあります。

反発係数と言ったりもします。

人間が勝手に決めたものです。あれば便利だってことです。
例えばそういうもので、他に何があるかと言えば、波の単元に屈折率というものがあります。世の中に屈折率というものがあるわけではありません。

しかし、
光がカクンと曲がった時に屈折率が1.2という風に決めましょうよ。
という風に人間が決めた。

ところが、便利に使えるためには、ちゃんと決めないといけない。適当に決めるわけにはいけません。
ですから、

それでは、3番目のテーマとして、はねかえり係数の式を取扱っていきます。
まず、
ということを考えたものです。

床があって、物体が速さvでぶつかったとします。
はねかえった時には、v‘になったとしよう。
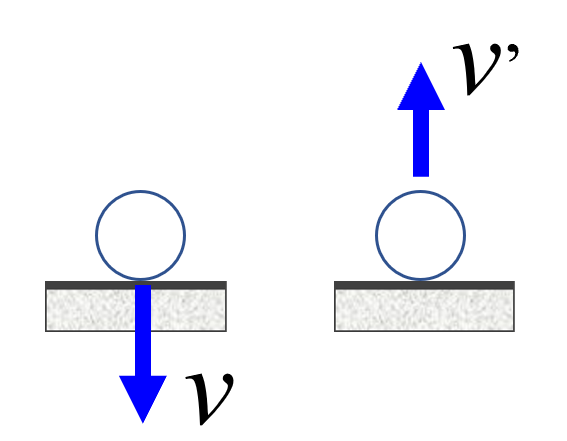
この時にこう決めたんです。
v‘はe倍のvだって。

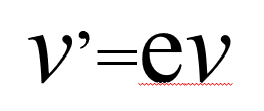
だから、当然、現象を考えてもわかると思いますが、eというのは、ゼロから1の間に入る訳です。
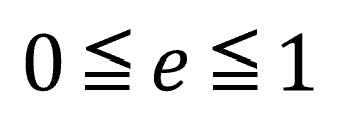
はねかえり係数が3とかだったら気持ち悪いでしょ。

そんなことは起きないですよ。ボールを下に投げつければ話は別ですが…

ただ、それだけのことです。
ところが、物理というのは超理想状態なんかも考えたりするから、ここにイコールが入っていたりする(e=1)。粘土みたいなものを考えれば、はねかえり係数0なんてこともありますねぇ。べたぁっっとなって終わり。
実際に1になるものってのはないですね。

ということです。
要は、はねかえり係数はと言われたら、e=v’/vとなるわけですねぇ。

こんな感じですねぇ。
ところが、こちらの計算は、速さでやっているんです。
向きを考えていないんです。



そうすると…、床に当たったわけです。
が~んってやってメリメリメリって入らないですよねぇ~。

ガーンってやったらはねかえります。
ということは、必ず向きは逆になります。
そこで、今までは、「速さがe倍になりますよ~」って言ってたのをどうするかっていうと、

いいですか。マイナスe倍です。
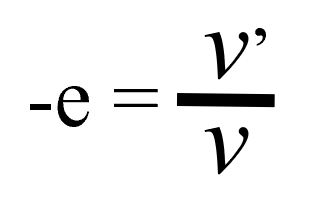
例えば、
10という速さできたものが、5ではねかえったよ~
という時に、
本来であれば、
下向きを正とすれば、マイナス5ではねかえったことになるでしょ。
だからここ(e)にマイナスをつけてあるんです。こうやって、速度に拡張するから、ここ(e)にマイナスがつくんです。
ですから、2つの式を混同している人がいますねぇ。


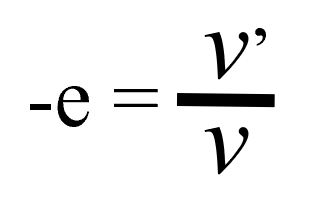

だから、どうやって決めたかってことがわかっていれば、こういうところでゴチャゴチャ悩む必要はないんです。自然と出てくることなんです。

それでは、最後です。
これはぇ、いつも相手が床とか壁とか限らないんですよ。

そうなってくると、いつも床とは限らない。
いつも衝突する相手が止まってくれているとは限らない。


この床が!
こうガーンとぶつかることによって動く。
それならねぇ、

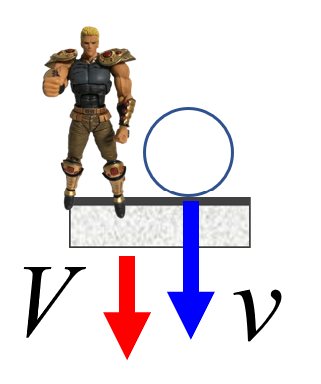
だから、これは床じゃないですよ。動くものですよ。
具体的に言うと、


それで、ガーンってぶつかった。
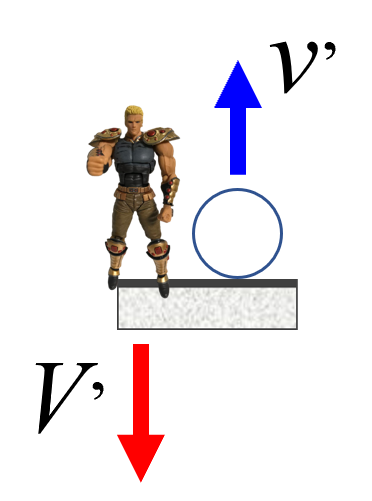

いつも床ばかりではだめで、床を一般の物体に拡張しようというわけです。

ということは、

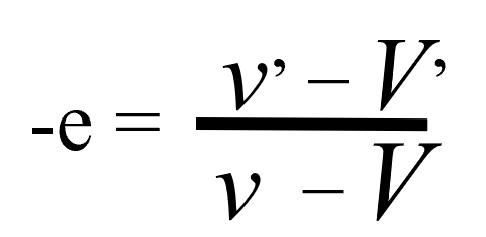
これでいいわけです。
引く順番はひっくり返しても大丈夫です。

それから人によっては、v‘-V’をマイナスe倍のv-Vとする人もいますが、それはどちらでも構わない。
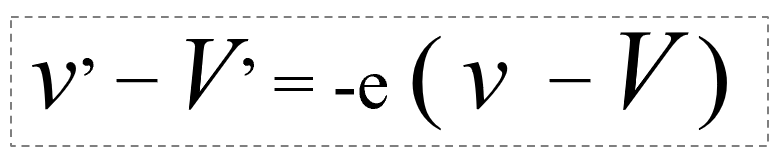
はねかえり係数のこの式、ただ単に丸覚えでは応用が利きません。

っていうような人が多いんです。

どこからそういうものが出てきて、
このマイナスって、いったい何を意味しているのか?
とか、
なぜはねかえり係数は原則として0から1の間に入っているのか?
とか、
そういうようなことを覚えるのではなくて、当たり前じゃないかと。
そらぁ、eは0と1の間に入ってるよと。

って、そういうような現実と結びついてくることが大切になってくる。
はねかえり係数についてもそうですが、物理の入試問題では、式が複雑になりやすいところがあります。
しかし、

そういったことを理解していないと、

これが見えてこないわけです。
多くの人は、ついつい、やり方を覚える。だから見たことある問題は解ける。

だから、

って思ってしまう。
しかし、

ちょっと勉強の仕方がまずかっただけなんですよ。
物理の勉強というのは、問題をたくさん解くことではないんです。本当に分かってもいないのに問題ばかり解いていてもダメなんです。

そうじゃないです。


って、確実に理解するんです。

さぁ、今回の講義はここまでとして、次回からは、運動量と力積に関わる問題を解説していきます。