目次
はじめに
今回は力学的エネルギーとその保存則について、基本事項を確認しながら、問題演習に重点をおいて解説していきます。
基本事項の詳しく知りたい人は、前回の記事を参考にしてください。
ここでは力学的エネルギー保存則にまつわる問題を中心に進めていきます。
基本事項の確認
力学的エネルギーとは、運動エネルギーと位置エネルギーの和のことです。
力学的エネルギー保存則とは、ある物体について前後の力学的エネルギーが同じである。

つまり、「前後の運動エネルギーと位置エネルギーの和が等しいという式」で表すことができるということです。
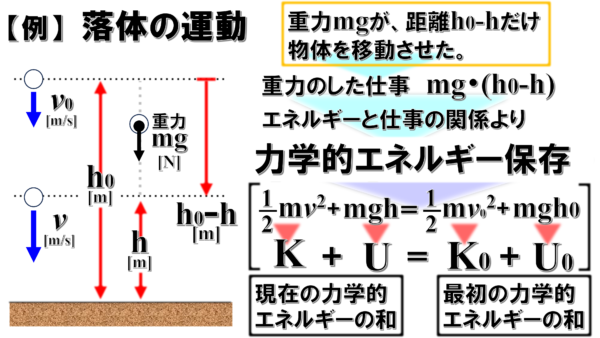
どうして、このような関係になるのかといった話については、こちらの記事を確認してください。
このように力学的エネルギーが保存されるためには、「物体にはたらく力が保存力だけであること」、もしくは「保存力以外の力がはたらいても仕事をしない」という条件が必要になってきます。

ここでは問題1で詳しく確認しながら進めていきます。
それでは早速問題の解説に入っていきます。
問題解説
問題1

これは力学的エネルギー保存則で解ける問題なのですが…

なぜ力学的エネルギー保存則で解けるのか…??
これが説明出来ないと、他の問題に対して応用が利きません。

そこで、この問題では基本の仕事とエネルギーの関係から解答までの道筋を辿っていきます。
それで、まずは物体はたらく力を考えて、点Aから点Bまで移動する時にそれぞれの力がどのような仕事をするのかを考えていきます。
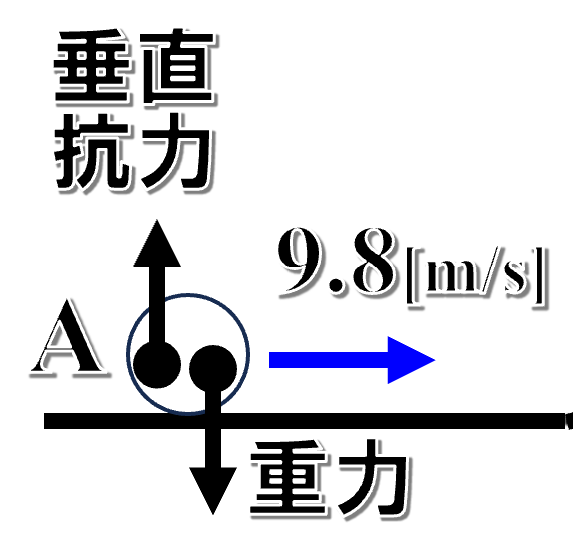

物体にはたらく力は、地球からの重力、そして床からの垂直抗力があります。
この時、垂直抗力がする仕事ですが、垂直抗力は点Aから点Bまでの区間では、どこにいても面に対して垂直にはたらく力です。

つまり、物体の進行方向に対して、常に垂直にはたらきます。
したがって、
垂直抗力は点Aから点Bまで移動することに対しては仕事をしない
と考えます。

したがって、垂直抗力がする仕事は0です。
次に重力です。重力は、地球上のどんな場所にいても下向きにはたらく力です。
したがって、水平面を移動することに関しては、さきほどの垂直抗力の時と同じように仕事は0になりますが…

曲面を登っている時は、曲面に平行な成分が何らかの仕事をします。
だから、この時の仕事を求めないといけないわけですが、面の角度は常に変化してますから、重力の曲面に平行な成分は常に変化します。

つまり、曲面を登っている時の重力は一定ではありません。
(仕事=力かける距離では求められない。)
そこで、仕事の原理を考えます。
物体を点Aから点Bに運ぶという事に関して、斜面や曲面、滑車などの道具を使えば、力は小さくなるけども距離は長くなるから、トータルでの仕事量は変わらない!!
というのが仕事の原理でした。

この時の重力のように、仕事量が最初と最後の場所だけで決まる力のことを保存力と言います。
したがって、ここでは仕事の原理を利用して、図の赤い矢印のルートで物体を運ぶことを考えてみます。
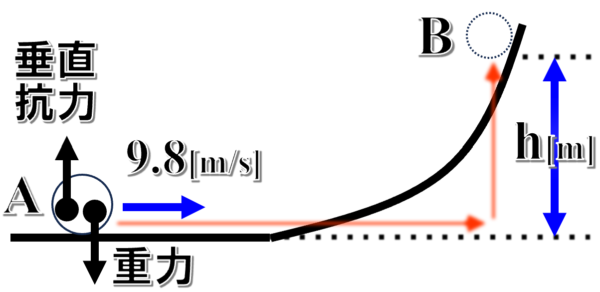
曲面を経由しても、赤いルートを経由しても、重力が物体にする仕事量は同じです。
だから、結局真上に上昇する時だけを考えると、「重力の大きさはmg」、「向きは進行方向と逆向き」です。そして、「高さはh」だから、重力がする仕事というのは負の仕事になって、ーmghとなります。

この時の高さhを求めないといけません。
そこで次に問題文を見てみると、物体は点Aでは速さが9.8m/sだったのが、最高点の点Bまで移動したとあります。


最高点ということは、これ以上前に進まない場所ということですから、この時の速さは0になります。
したがって、点Aから点Bまで移動することについて、仕事と運動エネルギーの関係を数式にしてみます。
すると、仕事の運動エネルギーの関係は‥‥

最初運動エネルギーが1/2m×9.82[J]だったけど0[J]になったのは、物体がーmgh[J]の仕事を受けたからだ。
このような意味の式が出来上がります。
この式からhを求めると、高さhは4.9mとなります。
これで問題の解答は終わりましたが、

なぜ、この問題が力学的エネルギー保存則で解けるのか…??
という問題がまだ解決していないので、そこのところを少し考えてみます。

力学的エネルギーが保存されるのは、物体にはたらく力が保存力のみである。もしくは、保存力以外の力がはたらいていても仕事をしない時です。
それで、今回の問題ですが、物体にはたらく力は重力と垂直抗力です。
その内、重力は保存力です。

垂直抗力は保存力ではありませんが、点Aから点Bまで仕事はしていません。
したがって、保存力以外の力がはたらいていても仕事をしていないので、力学的エネルギーは保存されます。

そこで、先ほど求めた仕事と運動エネルギーの関係式を点Aの力学的エネルギーと点Bでの力学的エネルギーという形に変形してみます。
すると、マイナスがついているものは逆側に持って行けば言いわけですから、
次のような式になります。
![]()
点Aでの重力による位置エネルギーが抜けていますが、点Aを基準水平面と考えれば0になりますから、確かに点Aと点Bの力学的エネルギーは保存されています。
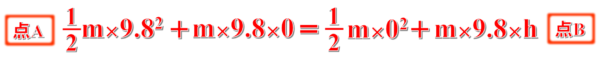
この式をといてもhが求まります。
仕事と運動エネルギーの関係式を、前後の力学的エネルギーの和に書き換えると、力学的エネルギー保存則の式になる。
※ただし、力学的エネルギーが保存される条件を満たしている場合のみ
①保存力だけが仕事をするとき
②保存力以外の力がはたらいていても仕事をしない時
このように仕事と運動エネルギーの関係から、力学的エネルギー保存則が成立するところまでを見ていきましたが、

仕事と運動エネルギーの関係は、保存力以外の力が仕事をしても成立しますが、
力学的エネルギー保存則は、保存力が仕事をしたら成立しません。
保存力以外の力が仕事をする場合については、次回の記事で解説していきますが、このような違いを理解することは、物理の学習を進めるに当たっては非常に大切です。

それでは、次の問題に進んでいきますが、力学的エネルギー保存則がどのように成立するのかについてはここで確認したので、次の問題からは詳細は省いて力学的エネルギー保存則を使って解答していきます。
問題2
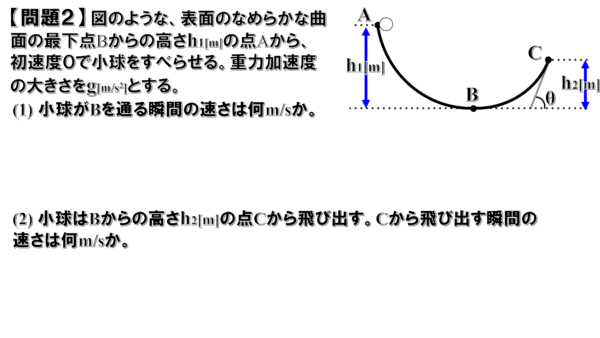
(1)
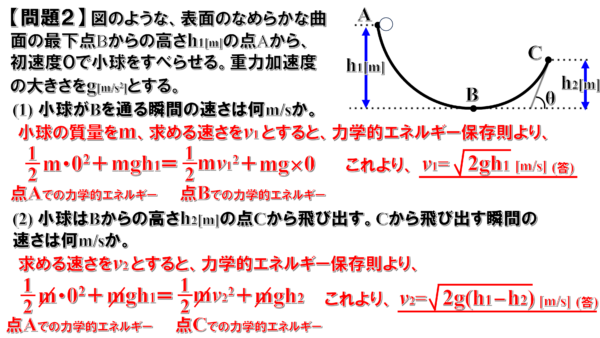
先ほどの問題と同じく、物体にはたらく力は重力と垂直抗力で、垂直抗力は仕事をしないので、力学的エネルギーは保存されます。
したがって、小球の質量をm、求める速さをv1とすると、力学的エネルギー保存則は次のようになります。

この式からv1を求めると、
![]()
となります。
(2)
これも先ほどと同じく、求める速さをv2 とすると、力学的エネルギー保存則は、次のようになります。

この式からv2を求めると、
![]()
となります。
(3)
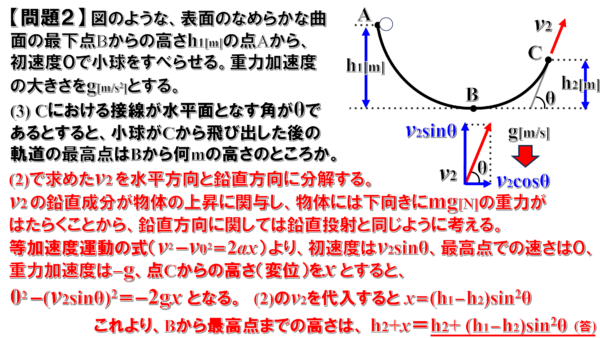
Cから飛び出した小球がどれくらいの高さまで到達できるかという問題です。
小球が到達する高さについて考えればいいので、Cからv2で飛び出した小球の速度を水平成分と鉛直成分に分解して、鉛直方向の運動だけを考えることにします。
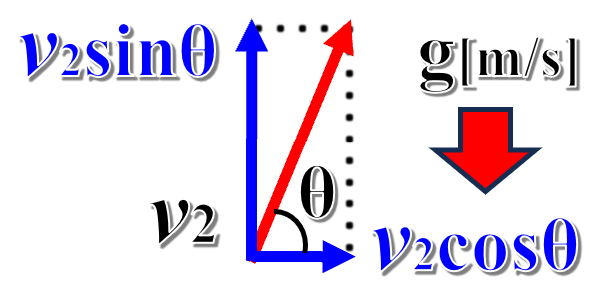
すると、v2の鉛直成分はsinθで、下向きの重力加速度を受けて運動するわけですから、鉛直投射と同じように考えることができます。
したがって、等加速度運動の式より、上向きを正の向きとして、
初速度はv2sinθ、最高点での速度は0、重力加速度はーg、点Cからの高さをx とすると、
次のようになって、(2)で求めたv2を代入して、xを求めると、
x=(h1ーh2)×sin2θ
したがって、Bから最高点までの高さは、
![]()
となります。
それでは次の問題です。
問題3

小球にはたらく力は、重力と糸の張力です。
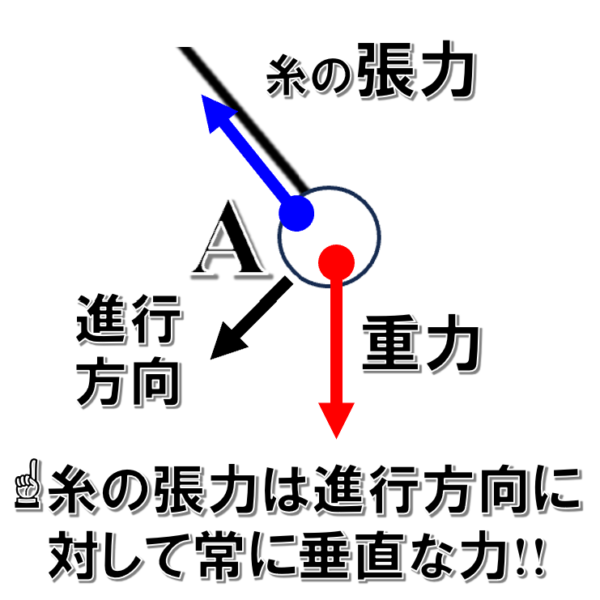
この時、小球が点Aから最下点Bを利用までに、糸の張力は常に進行方向に対して垂直方向にはたらいているので、仕事はしません。
重力は保存力です。
したがって、小球の力学的エネルギーは保存されます。
そこで、小球の質量をm、最下点を重力による位置エネルギーの基準とすると、力学的エネルギーの保存則は次のようになります。

点Aでの位置エネルギーですが、三角形の辺の比を使うと、最下点からの高さが1/5l になることがわかるので、mg×(1/5l ) です。
したがって、この式からvを求めると、

となります。

問題4
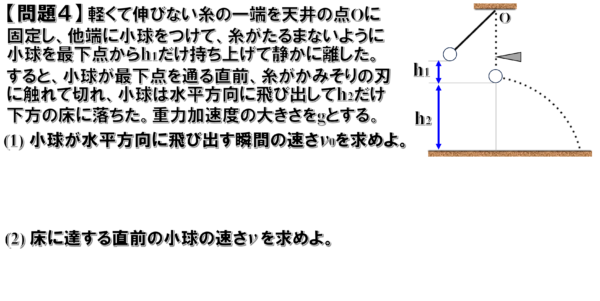
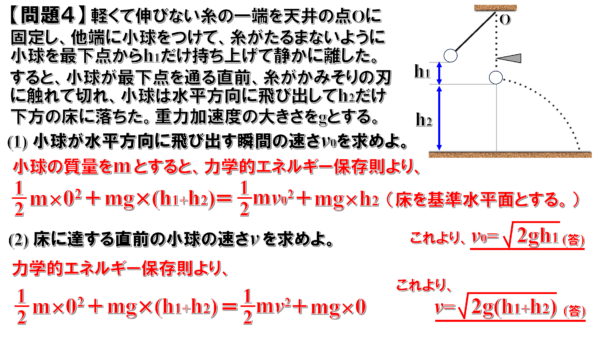
(1)
小球にはたらく力は、重力と糸の張力だけですから、先ほどと同じように力学的エネルギー保存則を考えます。
最初の位置と最下点については、小球の質量をm、床を基準水平面とすると、次の式が成立します。
![]()
したがって、この式からv0を求めると
![]()
となります。
(2)
最下点で糸が切れてから床に達するまでに小球にはたらく力は、保存力である重力だけです。
したがって、ここでも力学的エネルギーは保存されます。
よって、最初の点と床上での力学的エネルギーは等しいと出来るので、次のような式が書けます。
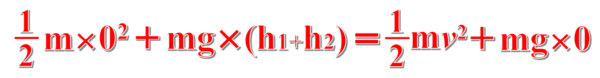
これより、vを求めると、
![]()
となります。
(3)
小球が最下点に到達すると、かみそりの刃によって糸が切断されて、水平方向にそのまま飛び出します。
その速度は、(1)のv0となります。
この時、小球にはたらく力は下向きの重力だけですから、小球の運動を水平方向と鉛直方向に分けて考えると…

水平方向の力は存在しないわけですから、運動状態は変化しません。
したがって、
水平方向へは、速度はv0のまま等速直線運動する
と考えられます。
そして、鉛直方向へは、初速度0で重力加速度gを受けて落下する…

つまり、自由落下すると考えられます。
そこで、鉛直方向にまず着目して、小球が床に落下するまでの時間をtとして、時間tを求めてみます。
等加速度運動の式から、
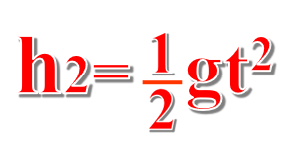
という式が出来て、
これよりtは、
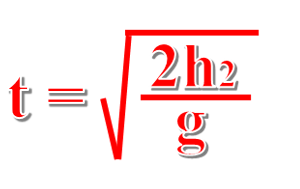
となります。
次に水平方向を考えると、小球は落下するまでに速度v0で等速直線運動するわけですから、
l はv0×t で計算出来て、(1)で求めたv0 と先ほど求めたtを
代入すると、最終的にl は、
![]()
となります。

それでは次の問題です。
問題5

この問題ですが、物体にはたらく力は、重力と垂直抗力、それからばねの弾性力です。
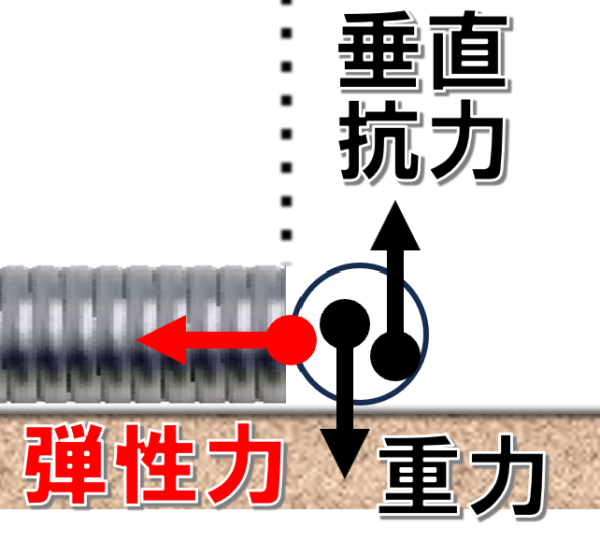
ここでは、ばねが伸びたり縮んだりすることで物体が左右に振動するので、進行方向に垂直にはたらく垂直抗力や重力は仕事をしません。

そして、ばねの弾性力は保存力に分類されるので、この時も力学的エネルギーは保存されます。
したがって、力学的エネルギー保存則より、次の式が成立します。
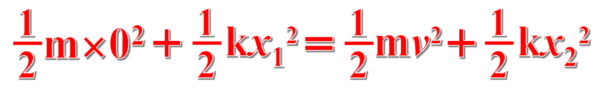

これより、vを求めると、
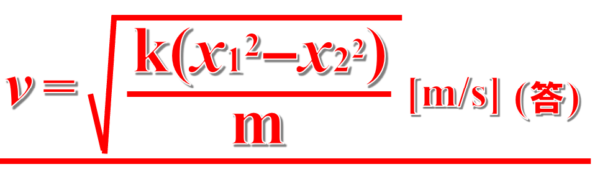
となります。
それでは今回の解説は以上となります。
次回は、保存力以外の力が仕事をする場合の問題について解説します。