
目次
はじめに
今回は水平投射について解説します。
水平投射について

水平投射とは、物体をある高さから水平方向に投げ出す運動のことです。
ある高さから物体を水平方向に放つと、物体は放物線を描いて飛んでいき、やがて地面に到達します。
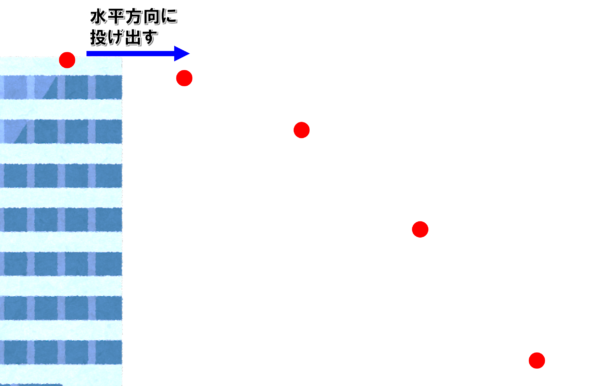

ここでは、物体には重力による加速度だけが関与しており、空気の抵抗力など、他の力による影響を受けないものとして、水平投射された物体の運動を見ていきます。
今まで学習してきた物体は一直線上を運動していましたが、水平投射された物体は平面上を移動します。
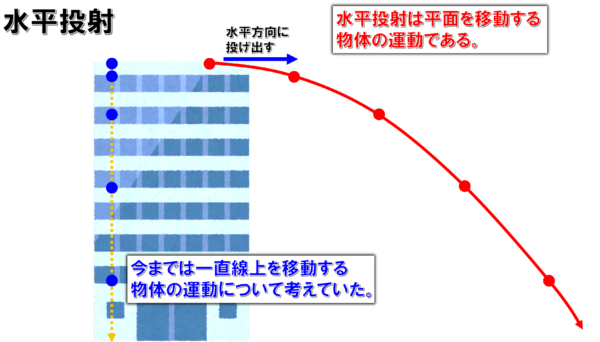

したがって、そのままの状態では、等速直線運動の式や等加速度運動の式に当てはめて物体の運動を解析することができません。
そこで、平面の運動ではx軸方向とy軸方向、それぞれの方向に対して、どれだけ物体の速さが変化したのか、どれだけ物体が移動したのかといったことを、別々に吟味していきます。
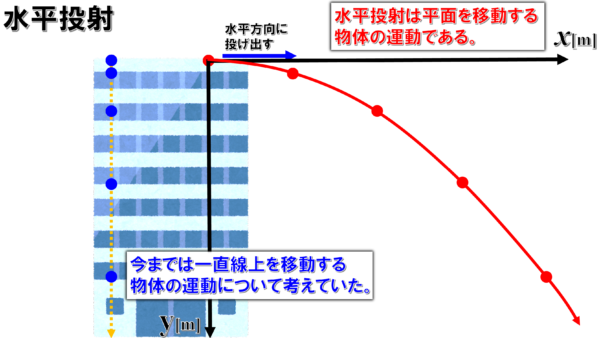
平面の運動の考え方
ここでは次のような例について考えてみます。
時刻t=0sで小球Aを自由落下させると同時に、同じ高さから小球Bを水平方向に初速度30m/sで投げ出します。重力加速度の大きさは9.8m/s2とします。
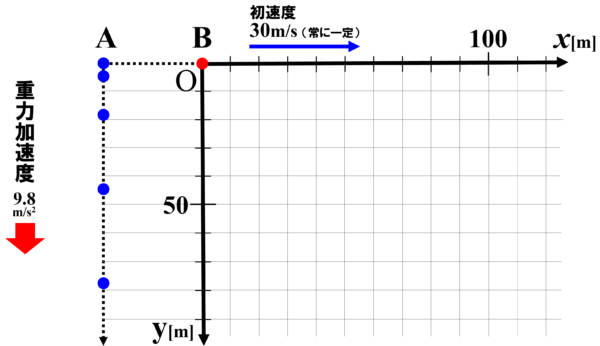
小球Bの初速度の向きにx軸をとり、鉛直下向きにy軸をとって、小球Aと小球Bの運動について考えていきます。
□自由落下運動についてはこちらをご確認ください。
小球Aの運動
小球Aは自由落下するので、図のy軸方向に1/2×9.8×t2の数式に従って落下していきます。
従って、1秒おきの位置を確認していくと、
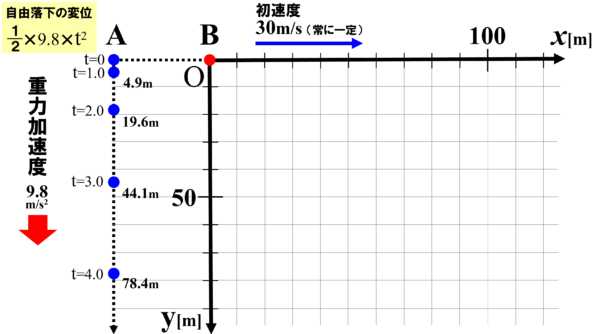
落下してから1秒後は、4.9m、2秒後は19.6m、3秒後は44.1m、4秒後は、78.4mの位置まで落下します。
小球Bの運動
次に小球Bを見ていきます。
小球Bは水平投射しているので、x軸方向とy軸方向を別々に見ていきます。
まず縦方向からです。
小球Bは縦方向に重力加速度の影響をうけて運動しています。

初速度30m/sというのは、水平方向への速度であり、小球が投げ出された直後は、縦方向の速度は0であることに注意してください。
したがって、縦方向だけの動きを見れば、自由落下運動と同じように変位することがわかります。
よって、小球Bの縦方向の変位をy軸上にプロットしていくと、図のようになります。
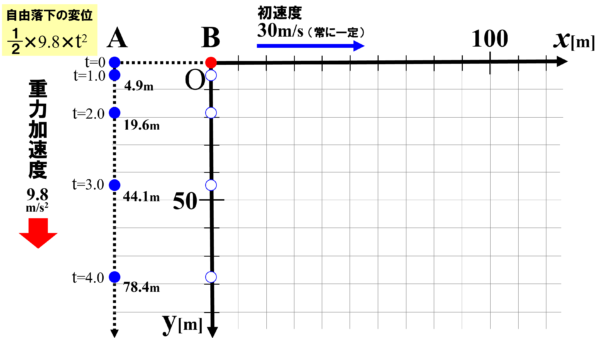
次の横方向の運動を見ていきます。
水平方向に30m/sの初速度で物体は、縦方向には重力加速度の影響を受けて加速するものの、横方向へは、速度を変化させる要素が存在していません。
したがって、物体は水平方向へは、等速直線運動していると考えられます。
よって、小球Bの横方向の変位をx軸上にプロットしていくと、図のようになります。
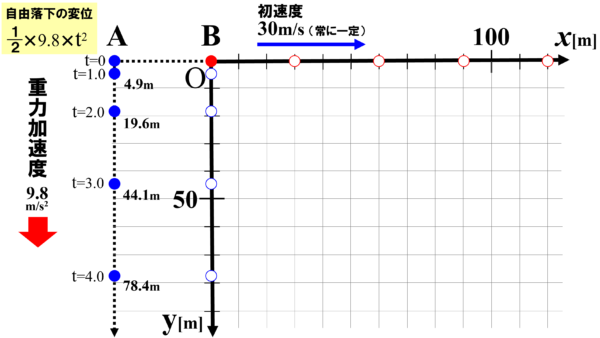
実際の小球Bの位置は、1秒ごとに縦方向、横方向の変位を合わせたものになるので、図の赤丸の様になります。
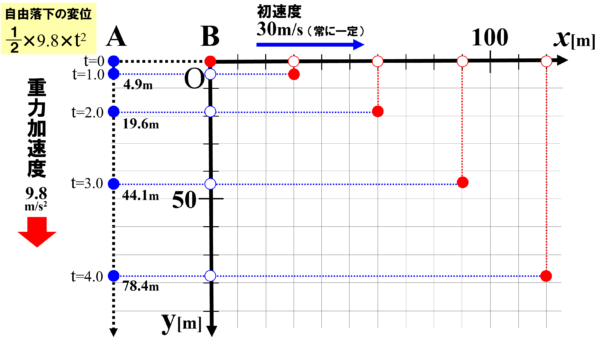
この赤丸を線で結んでいくと、水平投射する物体の軌道を描くことが出来ます。
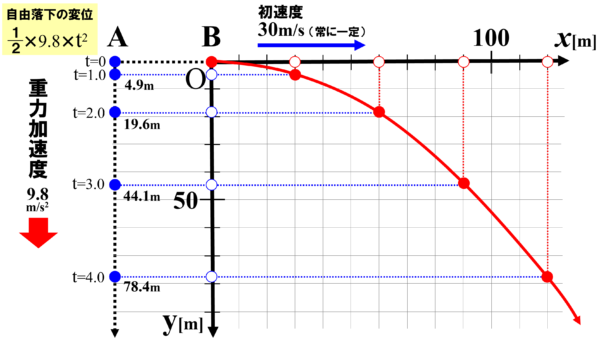

こうして、縦方向には自由落下、横方向には等速直線運動するものとして考えていくと、水平投射した物体の運動を吟味することができます。
水平投射の問題
それでは、ここで水平投射の問題を考えてみます。

(1)地面に落下するまでの時間は何秒か。
小球は、縦方向に自由落下運動するために、水平に投げ出された後、一定時間が経過すると地面に到達します。
従って、ここでは縦方向の運動について考えてみます。

縦方向に9.8m/s2の重力加速度の影響を受けて、自由落下運動するわけですから、まずは等加速度運動の式を使います。
(1)では地面に落下するまでの時間を求めないといけないので、ここで使用する等加速度運動の式は、v=v0+at、もしくはx=v0t+1/2at2のいずれかになります。
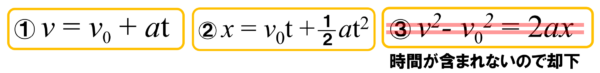
1つの目のv=v0+atについては、縦方向については初速度は0なので、v=atの関係からtが求められると良いのですが、現時点では、地面に落下する直前の速度vと落下するまでの時間tがわかりません。
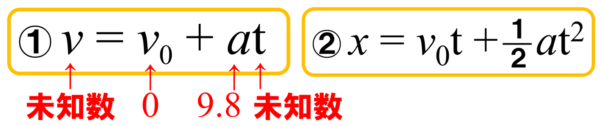

未知数が2つに対して、式が1つだけなので、このままでは時間が求まりません。
したがって、2つ目のx=v0t+1/2at2の式が使えないかどうかを考えてみます。
xは物体の変位であり、地面に落下した時の物体の変位xは問題文から下向きに19.6mであることがわかります。自由落下運動では初速度は0、加速度は9.8なので、これらの数値を代入すれば、時間tが求まりそうです。
そうすると…
![]()
このような式が出来上がります。
この式を解くと…

t=±2.0
マイナス2秒というのは、小球を投げ出す前になるので、解答から除外すると、
(1)番の解答は、2.0秒ということになります。
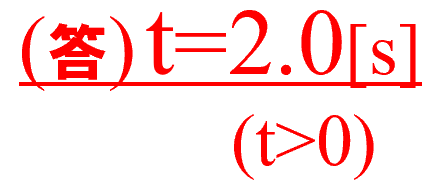
(2)(1)の間に、水平方向に何m進んでいるか。
小球が落下するまでに、水平方向に何m進んでいるかを考えないといけないので、横方向の運動について考えてみます。
小球は横方向には、9.8m/sの速さで等速直線運動します。
移動時間は(1)より2.0秒です。
これより、水平方向に進んだ距離は、速さ×時間より、
9.8×2.0で19.6m。

有効数字2桁で答えると、20mとなります。

(3)地面に落下する直前の物体の速さを求めよ。
平面の運動では、物体の速さvは次のように求めます。
まずは、特定の時間における水平方向の速度vxと、鉛直方向の速度vyを求めます。
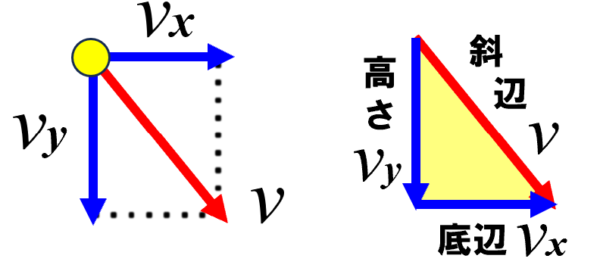
この時のv、vx、vy は、直角三角形の底辺と高さ、および斜辺の関係になるので、三平方の定理を用いるとvx、vyからvを求めることができます。
この手順に従って、今から地面に落下する直前の物体の速さを求めていきます。
まずは、水平方向ですが、水平方向へは9.8m/sで等速直線運動しているので、vxは9.8となります。
次に鉛直方向ですが、地面に落下するまでに2.0秒かかるわけなので、落下する直前の速度は、初速度0から9.8m/s2の加速度によって、2秒間加速したと考えると、19.6m/sとなります。
![]()
これより、vを求めると、vは22m/sとなります。

したがって、地面に落下する直前の物体の速さは、22m/sとなります。
















