(3)はじめに
それでは前回の鉛直投射の問題に引き続き斜方投射の問題を進めていきます。
■前回の講義
□自由落下運動と鉛直投げ下ろし運動は、こちらをご確認ください。
□水平投射については、こちらをご確認ください。
斜方投射の問題
小球を速さ19.6m/sで地面から斜め30°だけ上方に向けて投げ上げる。重力加速度の大きさを9.8m/s2として、以下の問いに答えよ。
問題の解答に入るまえに、まずはこの斜方投射の特徴を整理していきます。
この画像は、実際に投げ上げた小球の様子を一定の時間間隔で記録したものです。
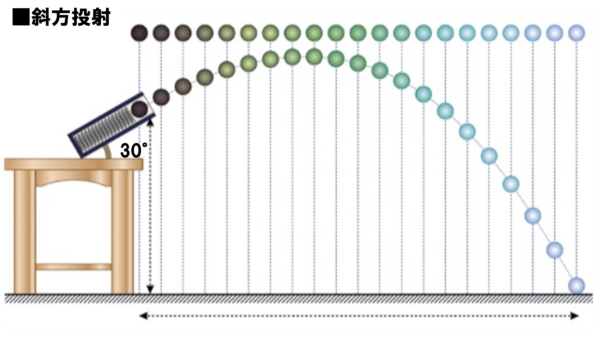
その上に等間隔につらなる小球は、投げ上げた小球の水平方向の間隔を記録したものになります。この図を見ると小球は等間隔で並んでいることがわかるので、水平方向では等速直線運動していることがわかります。
それでは鉛直方向はどのようになっているのかというと、斜めに打ち上げられた小球は、下向きにはたらく重力加速度の影響によって、徐々に減速し、最高点に達すると、やがて下降していきます。したがって、小球の縦方向の動きだけに着目すると、鉛直投げ上げ運動をしていることになります。
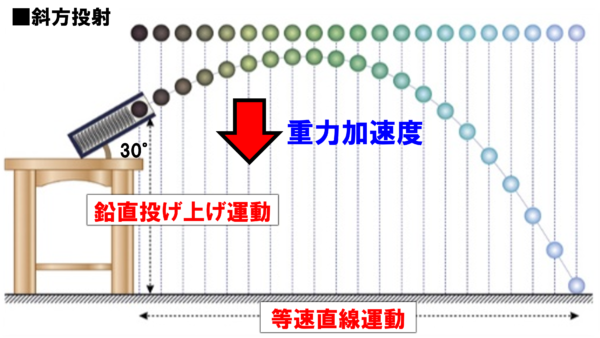

したがって、小球の運動は、水平方向には等速直線運動、鉛直方向には鉛直投げ上げ運動というように、縦横2方向の成分にわけて考えると非常にすっきりと整理できることがわかります。
これが、今回の問題を解くための手がかりとなってくるので、そのあたりのことをこれから実際に確認していきます。
(1)解説
(1) 初速度の水平成分と鉛直成分をそれぞれ求めよ。
地面から斜め30°上方に投げ上げた小球の初速度を水平成分と鉛直成分に分解する問題です。先ほどの説明を聞いていただければ、なぜこのような問が存在するのかが分かってもらえると思います。
求める速度は、水平成分を vx鉛直成分をvy とすると、図に示すように水平成分はvx=19.6cos30°、鉛直成分がvy=19.6sin30°となるので、答えは、水平成分が小数点第1位を四捨五入すると17m/s、鉛直成分が9.8m/sとなります。
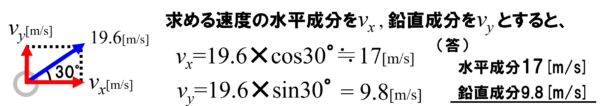
次の問題に行きます。
(2)解説
(2)小球が最高点に到達するまでの時間を求めよ。
小球の高さ、つまり縦方向の運動に関わる問題なので、鉛直投射の問題に置き換えて考えていきます。
最高点は、小球の速度の鉛直成分は0となるので、等加速度運動の式の速さと時間の関係式より、求める時間をt1とし、初速度は、(1)で求めたvy=9.8m/sを利用すると、0=9.8-9.8✕t1 、したがって、求める時間は1秒となります。
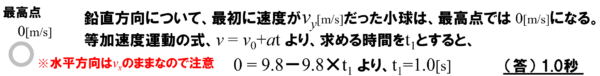
続いて(3)の問題です。
(3)解説
(3)小球が到達する最高点の高さを求めよ。
(2)で最高点に到達するまでの時間を求めたので、等加速度運動の距離と時間の関係式より、求める高さをyとすると解答は次のようになります。
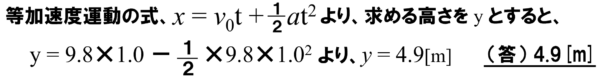
それでは(4)番にいきます。
(4)解説
(4)投げ上げてから再び地面に衝突するまでの時間を求めよ。
鉛直投射の問題で解説したとおり、答えは2秒と即答できますが、念のために等加速度運動の式を立てて解いていきます。再び地面に衝突するというわけですから、小球の高さが再び0mになる時間を求めればよいので、求める時間をt2とすると、解答は次のようになります。
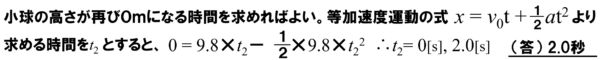
ちゃんと2.0秒という答えが出てきました。
それでは、最後の問題です。
(5)解説
(5)投げ上げた地点から落下点までの水平距離を求めよ。
ここでは、小球が地面に到達するまでに進んだ水平距離を求めるわけですから、等速直線運動の問題に置き換えて考えていきます。
小球は水平方向にはvxの速度で、落下点に到達するまでの時間、つまり2秒間移動するわけですから、求める距離をxとすると、x = 19.6cos30°✕2.0 で、小数点第1位を四捨五入すると、答えは34m となります。

これで問題の解説は終わりました。斜方投射の問題は、一見複雑にみえますが、水平方向は等速直線運動、鉛直方向は、鉛直投げ上げ運動というように、方向を限定して解いていけば、スムーズに解答できるようになりますので、 こういったところをよく整理して学習を進めてください。
それでは、今回の講義はこれで終了となります。お疲れ様でした。