はじめに
今回の講義では落体の運動について考えていきます。落体の運動というのは、地上から空中に投げられた物体の運動で、高校物理においては、自由落下運動や水平投射、鉛直投げ上げ運動や斜方投射がその代表です。
□自由落下運動と鉛直投げ下ろし運動についてはこちらを確認ください。
この章の授業では、斜方投射の問題が解けることを目標に学習を進めて行きます。
斜方投射とは、ボールを遠くに放り投げた時に放物線を描く運動のことを言います。これからは、この運動を理解していくことになりますが、その前に真上にボールを投げ上げる、鉛直投げ上げ運動から見ていくことにします。
□今から斜方投射の問題を確認したい人はこちらをご確認ください。
鉛直投げ上げ運動は、斜方投射の問題を解く時に大切になってきますので、しっかりと理解してください。
鉛直投げ上げ運動(鉛直投射)
鉛直投げ上げ運動は、等加速度運動に含まれる運動です。等加速度運動については、前回の講義で確認したので、いきなり問題を解きながら考えていくことにします。
小球を速さ19.6m/sで地面から真上に投げ上げる。重力加速度の大きさを9.8m/s2として、以下の問いに答えよ。ただし、鉛直上向きを正とする。
重要語句の確認
問題文に、重要な言葉が出てきたので順番に解説します。
まず重力加速度です。

加速度と書かれていますから、重力加速度は、加速度として扱うものであることはわかってもらえると思います。
それで、これは一体何なのかというと、小球を真上に投げ上げると、小球が最高点に到達して、やがて真下に落ちます。
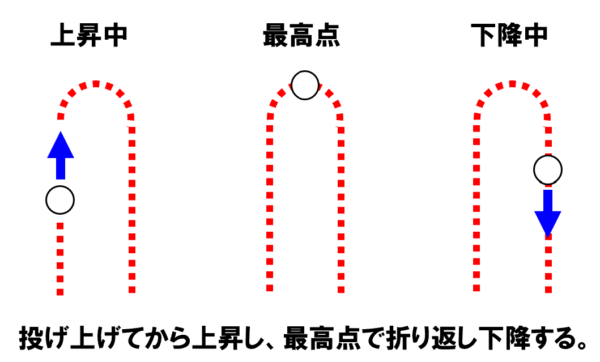
真上に進んでいた小球が、最高点で止まって、そこから真下に移動する。
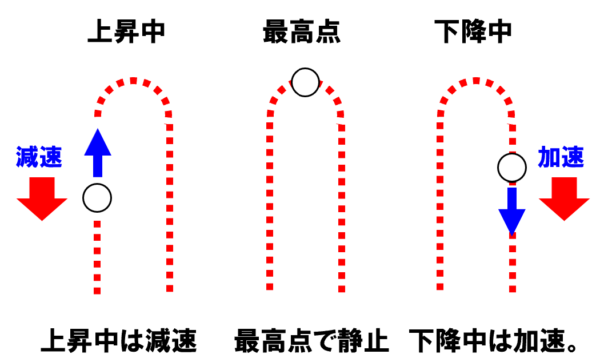
上昇している時には減速して、最高点で止まってからは、下方向に加速する。

小球を下方向に引っ張る力が働いていることに他ならないわけですが、皆さんは、この力の事を知っていますよね。
そうです。重力です。
重力によって生じる加速度のことを重力加速度といいます。
地球上での重力加速度は、ほぼ一定であることがわかっていて、その大きさは9.8m/s2です。
そして、次に「鉛直上向きを正」という言葉です。
前回の講義で、速度について前進すればプラスで、後退すればマイナスだと説明しましたが、今回の問題では、小球が上昇する方向を前進していると捉えるか、それとも真っ逆さまに落ちる方向を前進していると捉えるかで、計算式を立てる時のプラスとマイナスが逆転します。

そこで、問題を解くにあたって、どちらの向きを前進する方向とするか、その向きを指定するために「鉛直上向きを正」としています。
したがって、投げ上げた直後の小球は上向きに移動しているわけですから、速度は19.6m/sとして、一方、重力加速度は、下向きにはたらく重力が原因となる加速度ですから -9.8m/s2とします。
さぁ、それでは問題を順番に解いていきます。
(1)解説
(1) 投げ上げてから1.0秒後の速度を求めよ。
今回は等加速度運動の式を使って順番に解答します。

この問題は、1秒後という時間をヒントに速度を求めるわけですから、速度と時間の関係式v=v0+atを利用します。
そうすると、求める速度はvとして、vイコール、初速度は19.6m/s足すことの重力加速度は下向きに9.8m/s2で、上向きを正としているので、-9.8×1。これを計算すると、1秒後の速度は、上向きに9.8m/sとなります。
![]()

続けていきます。
(2)投げ上げてから3.0秒後の速度を求めよ。
この問題も(1)と同じように、速度と時間の関係式を使うと、vイコール19.6-9.8かける、時間は3秒後なので3とします。これを計算すると、3秒後の速度は-9.8m/s、したがって、下向きに9.8m/sとなります。
![]()
(3)小球が最高点に達するまでの時間を求めよ。

この問題ですが、直感的に答えが2秒になりそうなのはわかりますか?
1秒後に上向きに9.8m/sで、それから最高点を経由して3秒後には、下向きに9.8m/sです。
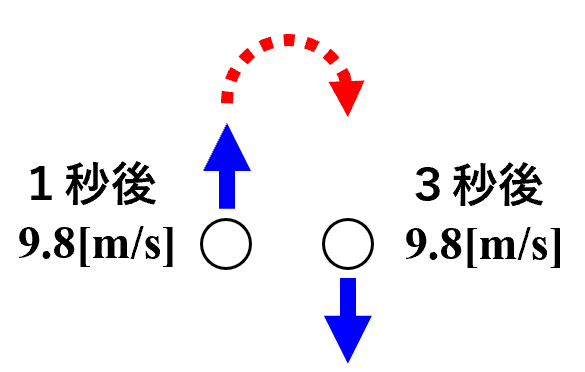
1秒後と同じ高さの位置に戻ってくるのが3秒後ですから、そのちょうど間の2秒後に小球は最高点に到達したのではないかという推測がはたらきます。

さぁ、果たして実際に2秒後という答えが出てくるのか?
実際に確かめてみましょう。
まずは、最高点到達する時の物体の運動状態を考えます。最高点というのは、上昇していた小球が進路変更して下降する瞬間です。この瞬間は、上向きにも下向きにも動いていないわけですから、この瞬間の速度は0になるでしょう。
したがって、小球の速度が0になる時間を求めます。そうすると、求める時間をtとして、(1)、(2)と同じく速度と時間の関係式を使うと、0=19.6-9.8かけるt。
したがってt=2。

ちゃんと2秒後という答えが出てきました。
それでは続けて(4)にいきます。
(4)小球が到達する最高点の高さを求めよ。
今度は「高さ」、つまり距離を求める問題です。
(3)で最高点に到達するまでの時間を求めたので、ここでは、距離と時間の関係式を使います。したがって、解答は次のようになります。

それでは最後の問題です。
(5)投げ上げてから再び地面に衝突するまでの時間を求めよ。
地面から投げ上げた小球が再び地面に戻ってくるまでの時間を求めるわけですが、これも(3)の問題と同じように考えることができます。

地面から投げ上げた小球が最高点に到達するまでに2秒かかるというわけですから、最高点から再び地面に戻ってくるも2秒だろうと予測できますね。
それでは実際に計算式を立てて解いていきます。この問題はどの式を使えばいいのかわかりにくいところではありますが、再び地面に衝突するということは、地面に戻ってくること、つまり高さが0mになるということを読みとれれば、(4)と同じく距離と時間の関係式でいけることが見えてきます。
したがって、解答は次のようになります。

これで鉛直投射の問題は終了しましたので、次の記事では本題の斜方投射の問題に入っていきます。