はじめに

今度はコンデンサーの合成をQ=CVを使いながら、直列の場合、並列の場合をそれぞれやっていきます。
こうやって見ればわかると思うんですが、どうしても教科書とか学校で教わる時は、
コンデンサーはコンデンサーで教わる。
抵抗は抵抗で教わる。
だから1つの時間の中で、コンデンサーと抵抗を同時にやるってことが非常に少ないんです。
これを同時にやってみると、

同じことやってるんだ!
ってことがすぐにわかります。
回路の解法③(コンデンサーの合成)
直列回路の合成
まずは、直列から行きます。


今、3つコンデンサーがあります。
Q=CVを3回立てなくてはいけません。
ところが、C1とかC2とかCがあるだけで、どうしようもありません。

何か少なくとも一つは、仮定しないことにはどうしようもないですねえ。

どうしましょう??
それでは、C1に+qクーロンの電荷が存在すると仮定します。

次に、ここの片仮名のエの字のところです。
もともと電荷はゼロだったとします。

すると、エの字のところっていうのは、どこにも繋がっていないのでトータルゼロでなければいけません。
だから、ここはプラスq。

じゃあ、反対側はマイナスq。

ところで、ここで私は何を使いましたか??
電荷保存の法則を使いました。

抵抗の合成では電流保存を使いましたねぇ。
そして、右側の回路では電荷をq運んだことには違いないから、こうなります。

それでは電位の関係式に行きましょう。

コンデンサーC1の電圧とC2の電圧を足したものは、電源の電圧Vに等しいですよね。
だから、電位の式は次のようになります。

Q=CVよりV=C分のqです。
コンデンサーの電気容量がC1で電荷がqだったら、C1分のq。
そして、C2だったらC2分のq。

ここで確認しておきたいことがあります。
この2つのコンデンサーの電場は、下向きですよね。

プラス1クーロンを持った人がこうとっとことっとこ上がっていくと、あーしんどいなぁ…

それは誰のせいだ!
って、

あんた(V)のせい!
ということで、この式が成立します。

それでは、もう一つの回路はどうなるか??
こうです。


2つの電位の式は同じでないといけません。
そうすると、最初の式のVをC分のqにしてやって…

両辺をqで割ると、


なんか抵抗の並列と式が似てますねぇ。
この式も和訳できません。


これは電位の関係です。

C1にかかる電圧とC2かかる電圧を足したものは、
Cにかかる電圧に等しいですよ!
って言ってるだけです。

なぜなら、それを一つのコンデンサーと見なしたのですから!

だから、みんな公式として、これを覚えてしまうんですが、やっぱり、1つ前の式が頭に入ってる方がいいです。
コンデンサーの数だけ、基本式Q=CVを立てながら

この基本式を大事にする。
基本式からどうやって解くかを見つけ出す。
そこが大事なんです。全部ワンパターンなんです。
並列回路の合成
それでは、次に行きましょう。並列です。


もう、今やってることの目的はわかってもらえますね??
ただ単に、解いてるだけだと思わないでください。
公式を導いているだけではありません。
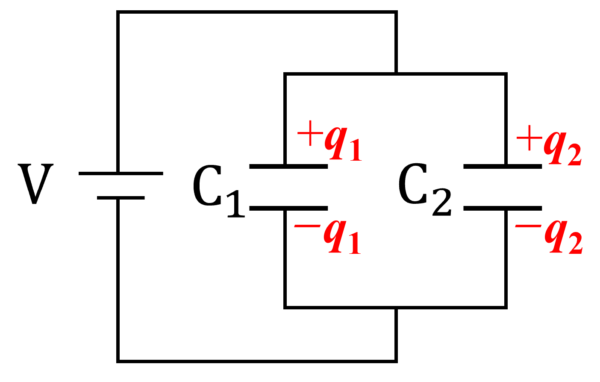

電位と言うのは、ポンプで電荷を持ち上げるわけですから、電池からしてみると、これが同じ回路というのであれば、蓄えられる電荷は、q1+q2クーロンとなりますねぇ…
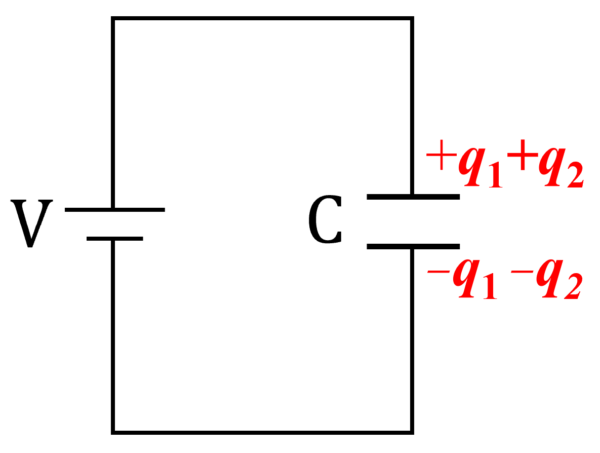
これから電位の関係式を考えていくわけですが、
電気容量C1のコンデンサーには、Vボルトかかってるわけですね。
こうなりますね。
じゃあ、この式にq1とq2を代入します。


q1とq2は仮定したものですから、消去していきます。

わかってもらえましたか…??
まとめ
それでは最後にまとめていきます。
こうやって、合成抵抗や合成容量の式を導くということをやってみた訳ですが、大事なのは公式を導くことではありません。

「一体、回路って何をすればいいのか!?」ってことを学んだんだ!
と言いました。
例えば今回の場合は、
2つのものを合成して1つのものと考えましょう!
っていうわけですから、

部品は3つあると考えればいいわけですね。
ですからV=IR。Q=CV。
みんな3つ立てたわけです。
だから、あとは、その関係式を持ってくればよい。
抵抗だと、電位の関係と電流。電流量保存。
コンデンサーだとQ=CVだから、電荷保存と電位の関係
ということになる。

そうなっていくと、いわゆる普通の回路の問題というのは、V=IR、Q=CV…

これを部品の数だけ、まず立てよう!
っていうわけです。

もし立てられなかったらどうするか?

その時は仮定するんです。

これ何かに似てませんか…??
例えば力学で、こういう風なものがあって、
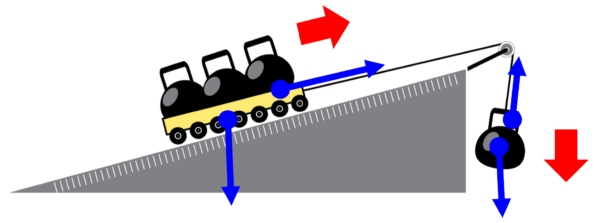
斜面上の台車の上に乗っかってて、縦に物体をぶら下げて台車を引き上げる時に、

台車について運動方程式立てて、
物体について運動方程式を立てる。
運動方程式というのは、物体個々について立てていくんだ。
という話を、物理基礎のところでしていると思います。

個々について立てていくんです。
アトウッドの滑車
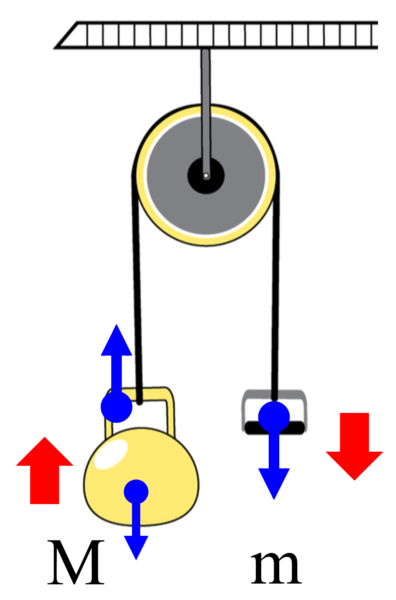
個々について立てます。

しかし、大抵与えられているのは、mとかMなんです。

そのおかげで、ma=…って式が作れるんです。

力学で言う、ma=F、それがV=IR、Q=CV。
これなんです。
個々について考える。
だから部品の数を数えなさい。
それだけ出来るようにしなさい。
作れるようにしなさいと。
つくれるようにするっていうけど、
抵抗とかコンデンサーが一般に与えられているので、
じゃあ、そこに流れる電流や、そこに蓄えられた電荷もしくは電位。
これを仮定しましょう。
仮定すれば、その時点でV=IR、Q=CVの式を作ることが出来る。

じゃあ、後はその連絡ツールです。

電流保存や電位の関係式。電荷保存や電位の関係式だとわかります。

では、何故そんなに電位の関係って大事なんでしょうか…??
よ~く考えてみてください。

電気部品にとって、ポンプというのはとても大切なんです。
ポンプという言い方で分かる通り、

位置エネルギーを与える装置っていうのは、非常に大事なんです。
例えば、最新式iPhoneを買いました。

あぁ、かっこいいなぁ。
便利だなぁ。

こんなことができるんだ。
こんなこともできるんだ。
しかし、もしも充電が切れていたら、それはただの荷物です。

それだったら、少々旧式でもいいからバッテリーが
ちゃんと入ってて、使えるやつがいい。
駄目なんです。ポンプがないと…。
電化製品はポンプが無いと何もできない。

これが電気の一番大きな弱点です。
例えば、物凄い誰も持っていないような電気自動車を買いました。


でも、実はうちの家には、専用のコンセントがないんです。
っていうのは、邪魔なだけですよね。

コンセントがあるからそういうものを買ってきて、使うと役に立つんでしょ??
要するに、電圧を与える装置…。

ポンプがない限りは、電化製品は一切何もできないんです。
それだけに回路の問題を解く時というのは、常に頭の中で、電位の関係式、もしくはキルヒホッフの第2法則もしくは回路方程式…

そういうものを最終的には立てていかないといけません。
それが連絡通路になっているんです!
ただ単に、

こうやって解けば良い!

ああやって解けば良い!
っていうような記憶に頼るようなことは、やめてください。
電流保存と電荷保存について
V=IR、Q=CV。

個々について式を立てていく…。
その後は関係式です。

だから電位の関係式立てましょう。
電位というのは、プラス1クーロンあたりの位置エネルギーということが分かっていますから、

プラス1クーロンの電荷をとことこと持って行って、あっ、高いとこ行ったとか言いながらやっていけばいいわけです。
そうやることによって、電位の関係というのは上手く行きます。
そして、今度はこっちです。

電流保存や電荷保存。
皆さんの中にも、

分からんでもないけどどうやってやるんだろう…??

でも実は、すごく簡単なんです。
それでは行きます。
電流保存についてです。流れがあるのに保存すると言ってるんです。

どういうところに注目をしていけばよいか??
ということなんですけども、
早い話が分岐点や合流点に着目をするんです。
例えば1つの例として、そこに I アンペア流れていた。
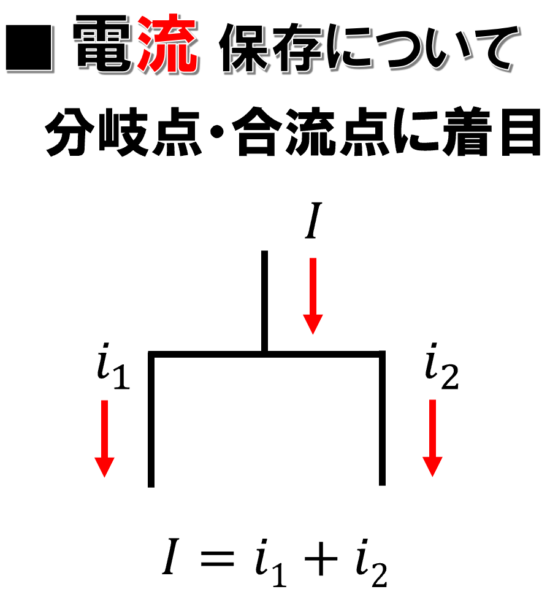

I = i1+i2が成り立っていますよ!
っていう

分岐点…。
これは簡単でしょう。
電荷保存、孤立金属に着目。
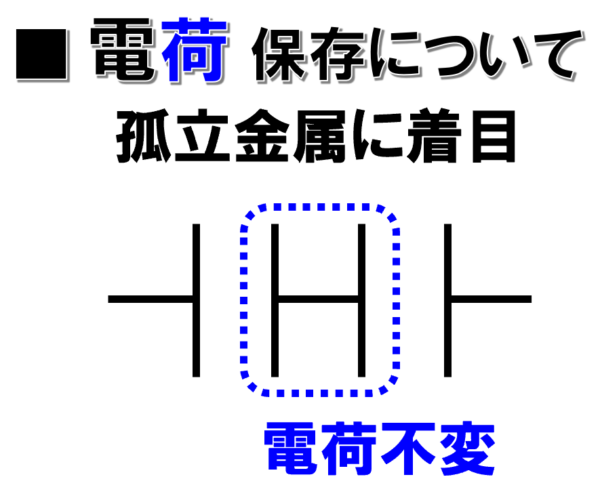

例えば。ここ(青の点線部分)、孤立してるでしょ!?
宙に浮いてるというか…、
繋がってないですからね。
回路の中でそういうところをちゃんと見つけること!
ということは、電流保存の方は大丈夫なんですよ。

ただ鉄板2枚持ってくるだけだ。

記号そのまんまだ!
と言いました。
だから、鉄板が左がに2枚ある。
そして右側にも2枚ある。
それがセットで結んであると…。

そこは、何者にも繋がっていない!
っていうことになりますね。
何者にもつながっていないということは、

電荷が入り込んでくることもなければ、電荷が出ていくこともないはずです。

そういう見方ができるかどうかですねぇ。
今日は回路の問題を解くために基本式というものを大事にして、そして、「その基本式からいかに解くか」という、その理由を考えながら解法を見極めていきました。そういう考え方をして、1つか2つ回路の問題にぜひチャレンジしてみてください。