はじめに

それでは、続きの問題に移ります。
□前半の解説

この後の解説では、問題の解法とあわせて、どういったところで差がつくのかも併せて理解していってください。
電場と電位の問題解説
(4)解説
(4)点電荷Qの符号は正負どちらか。
問題文に点Rは、x軸上正の向きに十分離れたとあります。

「十分離れている」というのは、実際どのくらい??
と言われると
例えば、電車に乗ってる時に十分離れて座ってくださいって言われたら、せいぜい1m2mくらいのものですが、

自宅から駅まで徒歩1mですって言われたら

滅茶苦茶近い!
ってなってしまいますね。

物理の入試問題で、十分にというのは、単刀直入に言うと「無限大」という意味と解釈します。
この問題の「十分離れた」というのは、-4qクーロンの電荷であったり+qクーロンの電荷の影響を受けないくらい十分に離れた場所ということになりますから、それは無限遠ということになります。


それなら、この時の電荷は正か負か??
と聞いているわけです。


片方が負の電荷であることがわかっているから、引力がはたらくためには、電荷Qは正でないといけない!
としています。

十分離れたところからは、点Aと原点の見分けはつかない。だから、2つの点電荷は同じ場所にあると考えてしまえ!
と言ってるわけですね。

とは言っても先生、こんな解法、試験本番で思いつかないよ!
っていう人は、(1)の解答を見て下さい。


だったら電荷qの符号も正でないといけない!
と結論づけることができます。
(5)解説
(5)点電荷Qが原点Oに最も近づいたときの、点電荷Qと原点Oの距離を求めよ。
公式だけしか覚えていない人には、

何だこれ!?
って感じの問題だと思います。

距離を求めるからV=Edか!?
って言っても、一様な場ではないからこの式は使えません。点電荷Qが原点に近付く間に電場も電位も変化しています。

じゃあ、クーロン力の式か位置エネルギーの式か…??
といっても、近付いた時の力も位置エネルギーも検討がつかないから解法の糸口がつかめない。

実はここで大切なのは、頭の中で等電位線がイメージ出来ているか!?
ということなんです。

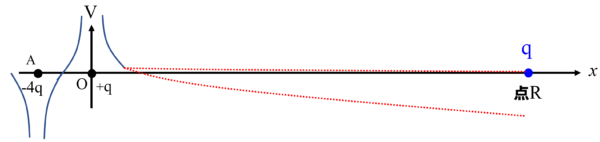

これ…ずっと下っていくわけではないですよね。
ずっと斜面だったら、点電荷が点Rから原点近づけないですから。

そこがどこなのかは、(1)と(2)の結果をグラフに書いたらわかるのですが、ここでは敢えて極力微分積分を用いた計算に頼らずに考えていきます。(原点から点Rの区間に必ず谷になる場所があることがわかればOKです。)
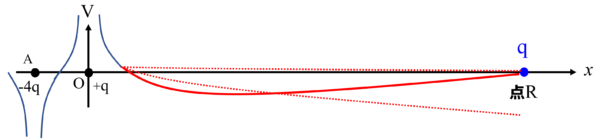

要は山が高いとか低いというのを目で見てわかるように図で表現したものです。
だから、高いところにボールを置いたら「スゥ―っ」とボールは転がっていくでしょうし、摩擦がなければ、そのボールは最初と同じくらいの高さまで上がってから、今度は逆方向に滑ってくることがわかります。

力学では、そういう風に考えて斜面に静かに置いたボールが、ここまで来た時の速さはいくらかというような問題を解いてきましたね。
ここでも同じことを考えたらいいんです。

ただし、今回斜面に置くのは、
qクーロンの正電荷ですが…
この問題は、「点Rに置いた点電荷Qが斜面を下ってから、原点Oに最も近づいた時の距離を求めよ!」と言ってるんです。

点電荷Qが斜面を下っていくと、この谷のところでは、止まれないから坂を上ってこの辺までくるわけだ。

それでは、点Rと最も近づいたところでエネルギー保存則を考えよう。
ただし、点電荷Qは質量と電荷を持った物体だから、力学的エネルギーに、クーロン力による位置エネルギーを含めないといけません。でも重力の影響は考えなくても良いって問題文に書いてあったら、重力による位置エネルギーは考えなくて大丈夫です。

だから、結局のところエネルギー保存則は、運動エネルギーとクーロン力による位置エネルギーに着目すればいいんだ!
ということで、点Rと最も近づいた点におけるエネルギー保存則を考えると、点Rは、点Rから十分に離れたところ、つまり無限遠だから位置エネルギーは0、静かに置いて転がり始めるところだから、運動エネルギーも0。
次、最も近づいた点では、ここで点電荷Qが静止するから運動エネルギーは0
そして、最も近づいた点をxとすると、x軸上の原点からx離れたところの電位は(2)で求めました。電位とは+1クーロンあたりの位置エネルギーです。今までの説明をまとめると次のような式となります。


この式をグラフにしたら、今、図で書いた線になるわけですからねぇ…。
「点Rからボールを静かに転がしたら、どこまで到達するか?」と言われたら、同じ高さのところになるでしょう。

そういう風に考えることが出来れば、容易に解答に辿り着くことが出来ます。
(6)解説
次は速さに関する問題です。点電荷Qが点Rから動き始めて、原点Oに行くまでの速さについて考えるわけですね。

速さの最大値はいくらか…??
ということで、これも(5)と同じように考えてみます。

ここしかないですよねぇ…。
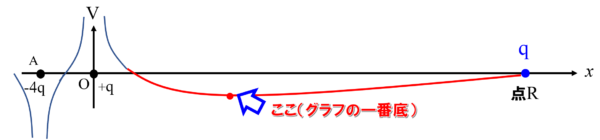
(5)では、点Rと最も原点Oに近づいた点に関するエネルギー保存則を考えました。

じゃあ、(6)では、点Rとここを考えればいいという訳です。
ここの運動エネルギーさえわかれば、エネルギー保存則からvが求められそうです。

しかし、vを求めるためには問題が1つあって、ここが一体どんな場所なのかがわかりません。
要は、ここの座標がわからないから、この場所の位置エネルギーが分からないんです。だから、まずはそこから解決していかないといけません。

原点にはプラスの電荷があるから、本来近づくことはないはずなんですが、その後ろにはー4qクーロンの電荷が控えているから、この電荷の影響を受けて引き込まれているんですねぇ…。
とは言っても近付いていくと、原点に+qの電荷があるから、この電荷の影響をもろに受けて反発力を受ける。

こういう力を受けながら、速さが最大になる点がここ!
(グラフの一番底)
ここが、どんな場所かと言ったら、斥力も引力も働かないわけですから、

点電荷にはたらく力が0になる場所!
ということになります。

力に関する式は(1)で求めました。
+1Cあたりにはたらく力、つまり、x軸上の電場は(1)で求めました。ですから、この式が0になるxの条件を考えると、この場所がどこなのかわかります。

これで、エネルギー保存則を考える準備が整いました。
求める速さをvとすると、
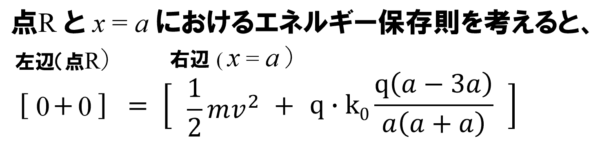
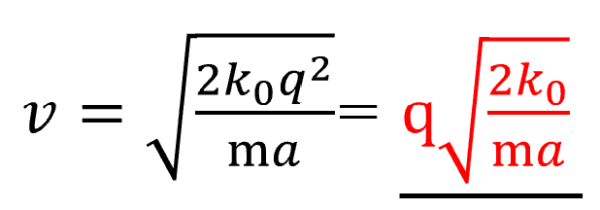

こういう問題だったら、皆さんも容易に解けると思います。
しかし、電気の問題になった途端に、それが出来なくなってします。

これって力学で言うところのどういう問題なのかなぁ…
って考えられる、力学に戻れるだけの実力です。