はじめに
それでは、前回の講義編で等加速度運動にまつわる知識を整理したので、今回は実際に問題を解いていきます。
■前回の講義
等加速度運動の問題
停止していた車が直線道路を一定の加速度で走行し始めた。車の速度は10秒後には20m/sとなり、ただちにブレーキをかけて一定の加速度で減速したところ、その地点から400m走って停止した。この時、以下の問いに答えよ。
問いに入る前に、問題文の状況を整理していきます。
まず最初止まっていた車が、10秒間加速することで、速度が20m/sになりました。その時の加速度はa、移動距離はxとします。
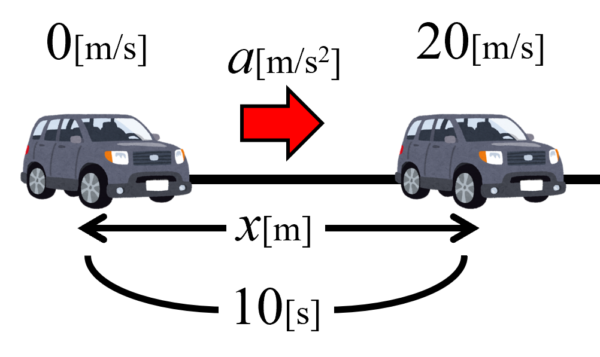
そして、そこから減速して、400m移動した時に止まったわけですが、減速している時の加速度をb、かかった時間をtとしておきます。
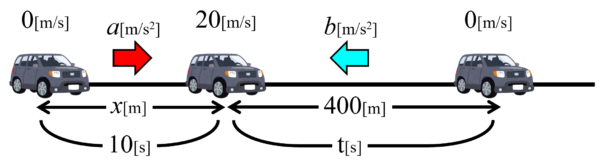
この状況において、次のような問題を解いていきます。
(2)ブレーキをかけるまでに走行した距離xを求めよ。
(3)車が減速している時の加速度の大きさbを求めよ。
(4)3において、加速度の向きを求めよ。
(5)ブレーキをかけてから停止するまでにかかった時間tを求めよ。
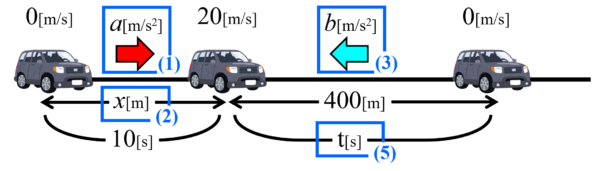
求めるべきものが確認できたので、今回は公式ではなく、v-tグラフを作成しながら解いていきます。(公式を使った解法は、次回の放物運動について考える時に活用していきます。)
最初車は停止していて、一定の加速度で走行し、10秒後には20m/sになったわけですから、ここまでのグラフは、このようになります。
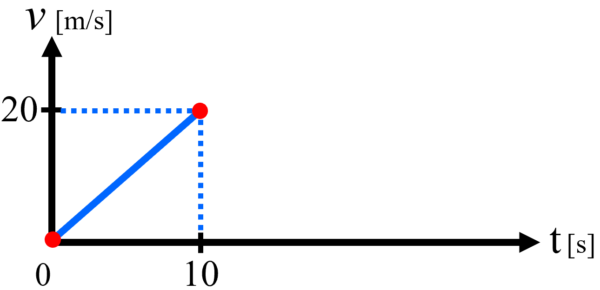
(1)解説
(1)の問題では、加速度aを求めないといけません。
単位時間当たりの速度変化、ここでは1秒あたりの速度の変化量。
これが加速度の定義になるわけですが、最初、止まっていた車が10秒後に速度が20m/sに変化したということですから、1秒間だと20÷10で2[m/s]速度は変化することがわかります。したがって、加速度の大きさは2m/s2になります。

(2)解説
(2)では、この時の走行距離を求めるわけですが、先ほど確認した通り、このv-tグラフの三角形の面積部分が走行距離に相当するわけですから、
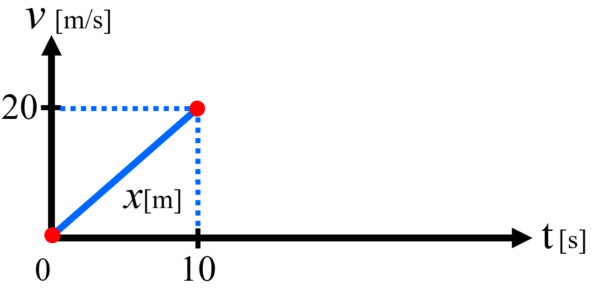
三角形の面積を計算すると、次のような解答になります。
![]()
(3)、(4)、(5)解説
残りの問題については、v-tグラフを完成させてから、まとめて解答していくことにします。
加速した車は10秒後にブレーキをかけます。停止するまでの時間がt秒なので、グラフの横軸の、t+10の位置に点を打って、この2点を結びます。
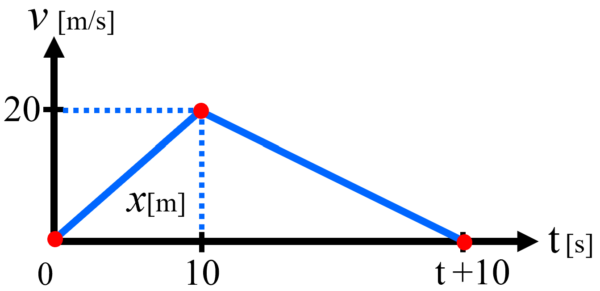
横軸はtではなくてt+10なので注意してください。10秒間加速してから、さらにt秒間かけて停止しているので、最初に加速した10秒間に、t秒を加えた位置に点を打ちます。
さて、この時、400m移動して停止したわけですから、この三角形の面積は、400になるはずです。
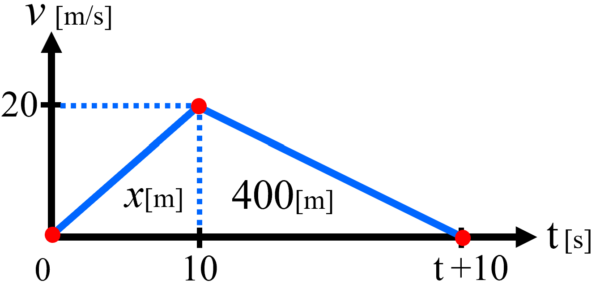
そこで、この面積をさっきと同じようにグラフの縦軸と横軸の長さで表すと、1/2×20×tです。
これが400に等しくなるわけですから、ここからtを求めると、t=40となって、(5)の停止するまでにかかった時間は40秒という答えが導かれました。
![]()
(4)については、車が減速しているので、加速度は進行方向と逆向きであることがわかります。
![]()
なので、残るは(3)の減速している時の加速度の大きさbを求めるだけとなります。
20m/sで走っていた車が再び停止するまでにかかった時間は、40秒であることがわかっているので、1秒間あたり20÷40で0.5m/sのペースで減速していたことがわかります。
したがって、(3)の加速度の大きさは0.5[m/s2]となります。
![]()
ここで1つだけ注意が必要なのですが、今回のbの解答については、「加速度の大きさ」を求められているので、答えは0.5[m/s2]となりますが、「加速度を求めよ」という「大きさ」という語句のない問いであったら、加速度の向きと併せて解答しないといけません。
その場合は、進行方向とは逆向きに0.5[m/s2]とか -0.5[m/s2]と解答してください。
さて、これで問題の解説は全て終了したので、今回の講義はこれで終了です。