
はじめに
今回は円運動にまつわる問題を実際に解説していきます。



使ってはいけないということではないですよ。

乱用しないようにする!

古代ギリシャ時代、アリストテレスは

地上界の運動は直線運動であるが、天上界の運動は円運動である!
と、地上界と天上界を明確に分けて考えていたところ、1600年代に入ってニュートンが月の運動から円運動を解析し、

地球上においてりんごが落ちるのと同様に、月も地球に落ち続けているんだ!
と結論付けて、地上界と天上界の境目はないという話をしました。
その話の流れから、等速円運動の加速度は a = rw2であったり、v2/r という表記を持ち、円の中心に落ち込むという意味を持つ式であると説明しました。

そして最後に慣性力の1つである遠心力という力にも触れ、等速円運動については、あまり遠心力を多用しないこと…
つまり、円運動を外側から静止して眺めた方がよいと伝えました。
そういったところも踏まえて早速、問題を見ていきましょう。
※問題文を掲載すると著作権に抵触するため、重要問題集をお持ちでない方は書店等でお買い求めください。
重要問題集45番の円錐振り子の問題
(1)(2)の解説
前回の講義において、

受験生の多くは、すぐに遠心力を書きたがる。こういう生徒は、もれなく単振動に苦手意識を抱く傾向にある。
と言いましたが、

重要問題集の解答でも遠心力を使って解いているんですねぇ…
困りました…

それだけ円運動が円の中心に落ち込み続ける運動であるということを理解していない受験生が多いということでしょうか…??
解答をみると、力のつり合いよりってあるんですけど、この問題では、ひもにつけたおもりを円運動させたんです。

物体が運動しているのに、まず力のつり合いから考えようってのは何か変ですよね。
物体の上に乗っかってみるのであれば、遠心力から力のつり合いについて考えるのでしょうが、そもそも遠心力は慣性力に含まれる力です。慣性力というのは、運動の法則を成立させるための苦肉の策です。
したがって、

特別な事情がない限りは、使用は控えた方がいい!
というわけです。
だから、まずは物体にはたらく力を整理して、運動方程式を考えましょう。
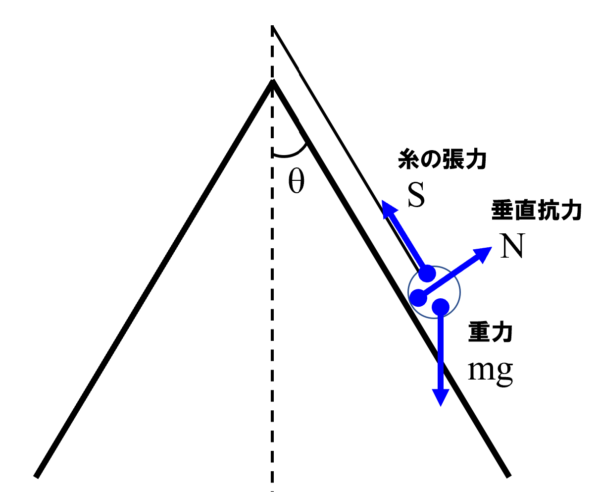
質量mの物体にはたらく力は、下向きの重力mgとひもに繋がっているから、ひもからの張力。そして、円錐面からの垂直抗力があります。それぞれをS、Nとします。
それで今回は「円錐面からおもりが受ける抗力が0である!」という訳ですから、Nは0です。したがって、おもりにはたらく力は、重力とひもの張力だけになります。
ここで、おもりの運動方程式を立てていくわけですが、このおもりが円運動しているんです。

円運動の中心は、ここですよ。
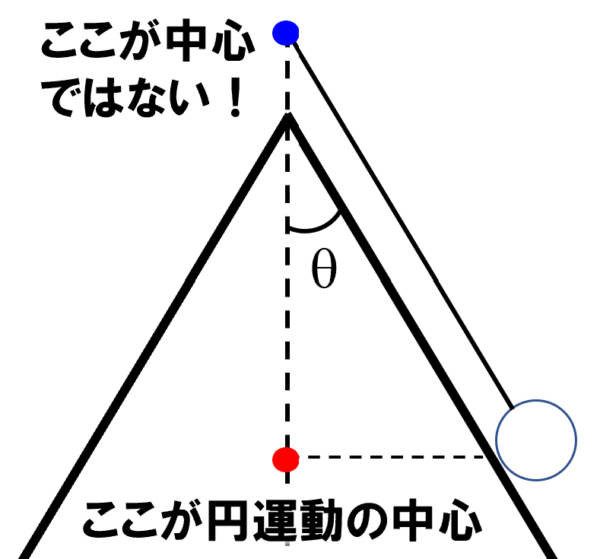
したがって円運動の半径は l sinθ 、円の中心方向にはたらく力は張力の水平成分ですからSsinθ と書けます。θ が90度だったら張力は真横にはたらくのでsinθであってます(cosθではないので注意)。

この力のせいで、おもりが円の中心方向に加速度 a で落ち込んでいるんですねぇ…
それでは実際に式を立ててみましょう。
質量mの物体に加速度 a を生じさせたのは、Ssinθである。
ただし、加速度は特別な表記を持っていて、a=lSsinθw2 と書けます。
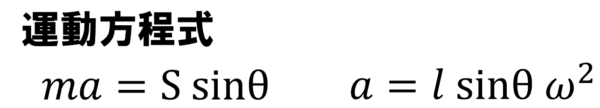
運動方程式からw2 を求めるわけですが、

ひもの張力Sがわからないですねぇ。
しかし、ひもの張力の水平成分は、おもりにはたらく重力とつり合っていますから張力Sは…
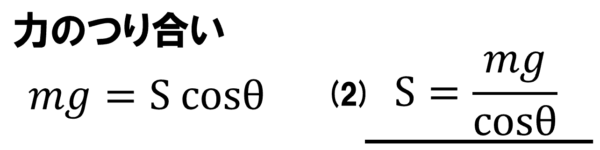
ですねぇ。ここで2番の答えが出てきました。
そして、このSを運動方程式に代入してw2を求めると、w2は、
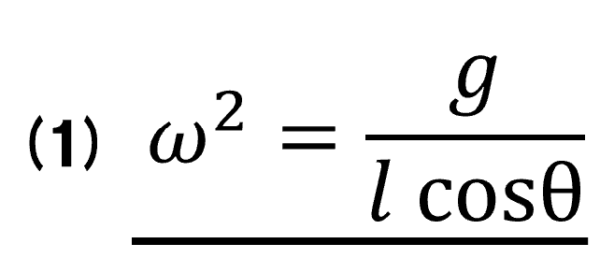
となります。

何も難しいことやっていませんよねぇ…??
皆さんは既に物理基礎で、こんな問題を解いてますよ。

斜面におかれた物体があって運動方程式を立てる時に、力を加速度の方向とそれに垂直な方向に分解したじゃないですか!?
あれをやっただけですよ。
加速度の方向とそれに垂直な方向に力を分解してから運動方程式を立てた。
(3)(4)の解説
それでは、続きの問題に移っていきます。
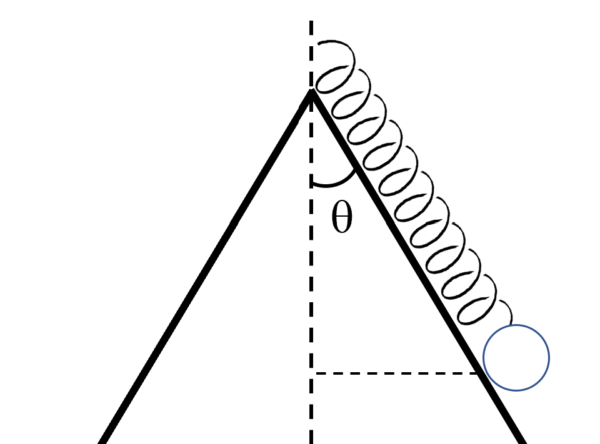

今度はひもに代わって、おもりにばねがつながれているんですねぇ。
したがって、おもりにはたらく力は、先ほどのひもの張力のところがばねの弾性力に代わります。自然長 l のばねの長さが r になっているので弾性力の大きさは、
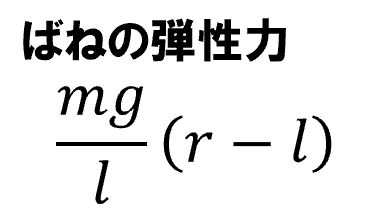
となります。
先ほどと同じようにw2を求めるわけですが、今回は抗力が働きますから、そこにも注意をはらいながら、まずは運動方程式を立てていきます。
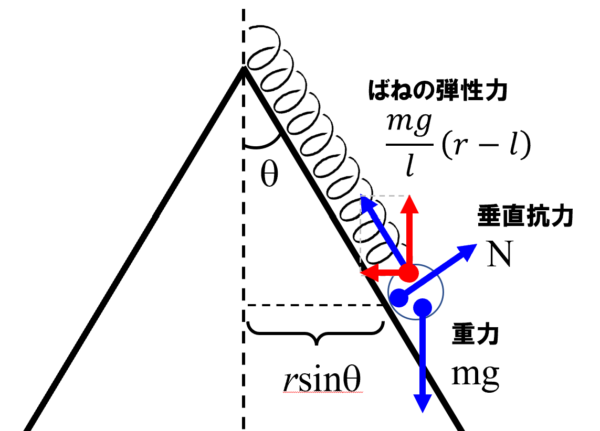
■弾性力の水平成分
![]()
■弾性力の鉛直成分
![]()
この時、円運動の半径は、rsinθ ですから、運動方程式は、質量mの物体に加速度aを生じさせたのは、弾性力の水平成分と抗力の水平成分が働いたからだ。
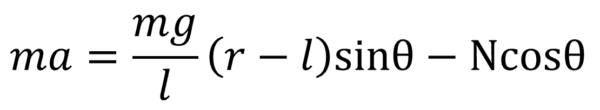
この時、加速度は
![]()
と書けますねぇ。
抗力の水平成分はNcosθですが、もしも斜面がぺたんとなったらθ=0で、抗力の水平成分はそのままNになります。θ=90度の時は、がばっと斜面が真上開いてるわけですから抗力がはたらくことはありません。したがって、その時の水平成分は0であっています。

sinかcosかで迷った時は、極端な時を想像してみて確認してください。
それでは続きに行きます。
ここでは垂直抗力Nがわかりませんから、鉛直方向の力のつり合いについて考えましょう。
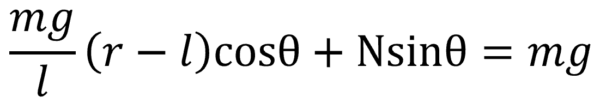
そうすると、ここからNが求まりますねぇ。このNは後で、運動方程式に代入して、計算することになるので、後々のことを考えて、ばねの弾性力のmg/lで括り出して書きます。
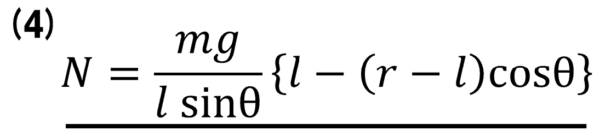
これが(4)の解答になっています。これを運動方程式に代入すれば、w2が求まりますが、計算がやや複雑なので、途中式を確認しておきましょう。
![]()
この途中式のsin2θの項とcos2θの項。
ここは同じですよね。
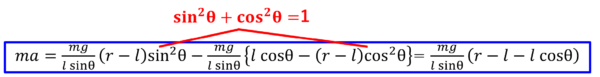
sin2θ+cos2θ=1と変形できますから、最終的には、( r - l )ところだけが残ります。
したがって、最終的にw2 を求めてやると次のようになります。
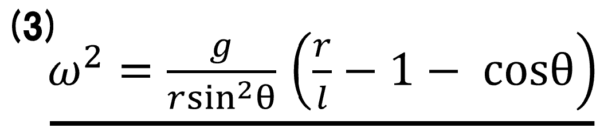
これが3番の答えです。
計算ミスさえ気をつければ、基本的にやっていることは、1番2番と同じです。
(5)(6)の解説
さぁ、それでは残りの問題に移りましょう。
(5)の問題は抗力が0の時ですから、4番の式にN=0を代入すればrが求まります。
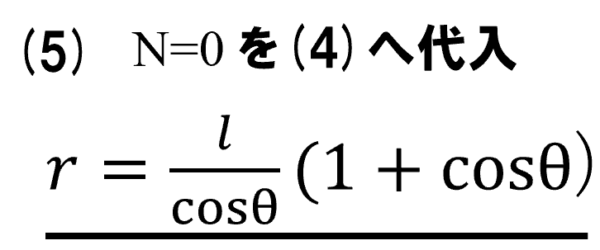
そして、求めたr を3番で求めたw2 に代入すれば(6)が解けます。
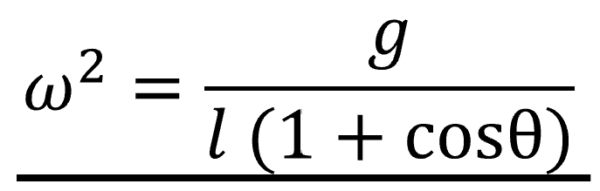

これで全て解けた~!!

ちょっと待ってください。

N=0の時のw2 は、さっき求めましたねぇ。

(1)の問題です。
(1)の解答を見てみると
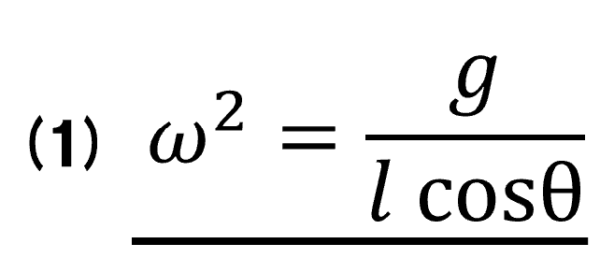
「w2は、重力加速度と角度とひもの長さl によって決まる!」と書いてありますねぇ。
もう一度言いますよ。

w2は、重力加速度と角度と長さだけで決まる…。
ということは、重力加速度と角度は変わっていませんねぇ。長さが l から r になっただけです。

じゃあ、(1)の l を r に変えてみましょう。
そうすると
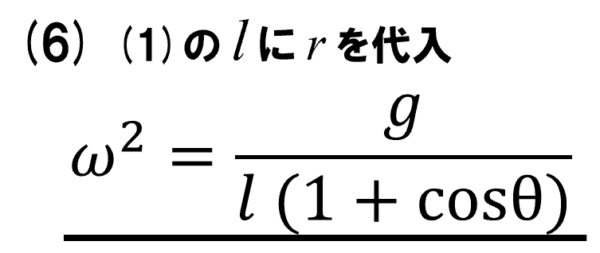
出来ましたねぇ。

こういう所を見抜けるかどうかでも差が出てきそうですねぇ。
w2は重力加速度と角度と長さによって決まるということは、引っ張ってるものがひもであろうがばねであろうが関係ないということですね。

問題なのは、引っ張っているものの長さであると…。
こういう計算が出来るようになると、問題の流れに沿って(3)で求めたw2に r を代入し、求めた(6)の答えとダブルチェックができるから計算ミスするリスクがなくなりますよね。

求めた解答が、どのような意味を持つのか吟味することも大切です。
さて、これで今回の解説は以上となりますが、遠心力を使った解き方というのは、常に物体の上に乗っかっているから、遠ざかるわけでも近づくわけでもない。

つまり物体が静止していると考えて力のつり合いの式を立てることになります。
静止している物体を扱うことになるから、どの方向に力を分解してもつり合いの式は成り立つんです。
だから、ある時は斜面の方向に力を分解したり、ある時は鉛直方向に分解したりと、いろんな方向に分解出来てしまいます。
それ故に特定の問題を解くためだけの解答になってしまったり、ひどい場合はでたらめに力を分解して頭の中がこんがらがってしまうことがあります。

だから、おもりの上に乗っかるのではなくて、おもりの外から円運動を眺める。

まずは円の中心に落ち込む方向に運動方程式を立ててみる
という風に、本質的というか一貫した解法で臨めるから、そこには迷いがありません。円運動における力の関係式を用いた解法、この問題を通してよく理解してください。



















