はじめに
それでは、万有引力に続いて、もう一つやっておかなければならないことがあります。
それが、万有引力による位置エネルギーというものです。
これはかなり難しい内容です。
万有引力による位置エネルギー
このように書くことができます。
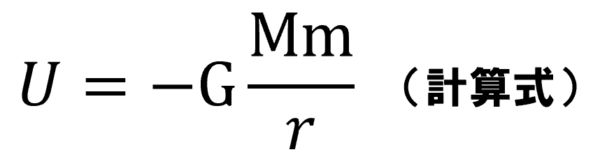
これは計算式です。万有引力の式をｒで積分しただけであることを知っておくと覚えやすいです。皆さんにとっては、位置エネルギーの式をｒで微分して、万有引力の式になったと言った方が数学的にわかりやすいかもしれません。
計算のことは一端置いといて、この位置エネルギーというのはなのでしょうか??
皆さんにとって一番身近な位置エネルギーはｍｇｈでしょう。
物理基礎で教わりました。
重力による位置エネルギーがｍｇｈだということを知らない人はいないでしょう。しかし、どうしてｍｇｈなのって言われた時に、さっと答えられる人はなかなか少ないです。
なぜ重力による位置エネルギーがｍｇｈなの…??
ｍｇに逆らってｈだけ持ち上げたからですね。
エネルギーというのは、我々にしてみれば能力という風に考えれば良いわけです。
例えばここにボールがあります。質量ｍとします。それが、私の手のひらに乗っかっているんです。ボールは落ちません。ところが、これを手で持ってｍｇに逆らってｈだけ「ぎゅ～っ」と持ち上げます。それから手を離せば、ボールは手の上に落ちることが出来ます。要するに落下能力を持ったという事です。
でも、ただのボールです。ボールが勝手に能力を持つわけがないんです。そんなことになったら気持ち悪いです。ずーっと置いといたら勝手にボールが動き始めたとか、そんなことは起きないんです。生き物であれば、ご飯でも食べせておけば、だんだん能力は増えます。しかし、私たちが扱っているのは「物」です。勝手に能力が増えたりはしません。
では能力が増える時というのは、どんな時でしょうか？?
それは、誰かが何かをしたときです。
だから私の手のひらで止まっていた、落下能力なんかなかった。だけど、私が重力に逆らってｈだけ持ち上げるという仕事をしたがために、手を離すと落ちるという能力を持つことが出来た。
では、この能力は？ ボールが持っている能力はどのように判断すれば良いの??
それは私がした仕事分です。
それが能力になったと考えればいいわけです。
ここまではいいですよねぇ･･･。
それでは、これもそうです。
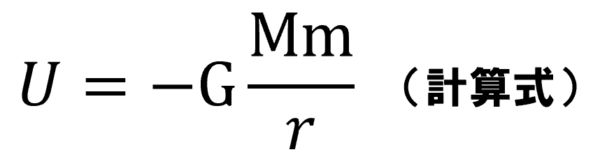
位置エネルギーの式にマイナスがつく理由は…??
ところが、そうやって説明した後に…
位置エネルギーが負ってどういう意味っすかぁ…??
という質問を受けます。
別にどういう意味もこういう意味もないです。これは負なんです。
例えば、今私が「高さｈのところまで持ち上げて離した」という話をしました。
もしも、手のひらから下げたらどうなるんですか？
ｍｇには逆らってないです。むしろ従っています。だから、最初に位置から見れば落下能力は負なんです。基準となる位置から見たら落下能力を使って無くなってしまったから、そういう言い方をしているだけです。
基準となる位置から見たら…
と言いましたね。必ず、基準が必要です。
位置エネルギーが０となる位置です。
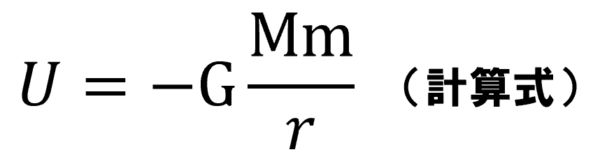
これが０になるんです。ただしGは０ではないです。Mも０じゃないです。mも０じゃないです。
それじゃあ、この式を０にするためには、どうすればいいか…？
ｒを無限大にするしかないんです。
したがって、位置エネルギーの基準は無限遠です。
ますます、話がわからなくなってきたかもしれませんが…
大丈夫です。今から、ちゃんと説明します。
私の質量ｍで、床の上に立っているとします。
床を基準にしましょう。そうすると、今の私の位置エネルギー０です。
私が住んでいる家はマンションの４階にあります。エレベータに乗って４階まで毎日上がってくるんです。
それでは、１階を基準にするとどうなりますか…??
それは、この床がなかったら大変なことですよねぇ。私は落ちてしまいます。
私は、今位置エネルギーを持っているんです。
エレベータにもらったんです。
エレベータに仕事をしてもらったんです。
スーパーの買い物から帰ってきた時に、エレベータにグァ～ンってあげてもらったんです。そのおかげで私は、落下能力を持っているんです。
ここまでは、いいですよねぇ。
この部屋の床を基準にすると、私の位置エネルギーは０です。だけど、ここは４階です。1階を基準にすると、私は大きな位置エネルギーを持っていることになるんです。
基準の取り方によって違うわけですねぇ…。
この家は、マンションです。８階まであります。
８階を基準にするとどうなりますか？
私の位置エネルギーは、８階よりも低い位置にあるわけですから、負です。
それじゃあ、８階より上の屋上を基準にすると…??
もっと大きな負です。
そうですよねぇ。
今度は、東京タワーのてっぺんを基準にすると…??
もぉ～っと大きな負です。
それじゃぁ、地球を脱出して、は・る・か・無限遠を基準にすると‥‥??
もぉ～～～っと大きな負になるでしょうね。
ほら、簡単だったでしょう。
どうってことはないんです。どこを基準にするかってだけの話なんです。実際には積分で出ているんです。大体、力がどれくらいの距離はたらいたかという概念でやっているわけです。
力を距離で積分するという事をやっているわけです。
だから、ｍｇｈというのは、ｍｇを距離で積分しているんです。
そういう考え方になっているわけです。しかし、これ（＝万有引力による位置エネルギー）は場所によって力が違うので、そうはいかないわけです。だから積分するんです。
積分することについては、高等学校の範囲ではこだわり過ぎる必要はありません。
それよりは、
なぜマイナスになっているのか？
というところが、理屈として説明できなければいけません。
こういう表記を持っていて、位置エネルギーの基準は無限遠です。
はるか遠くの無限遠なんです。
だから、負の位置エネルギーになっているんです。そのような考え方をちゃんと持てなければいけません。
これでいいですね。
仕事とエネルギーの関係から考えてみる。
まだまだ続きます。
今から、図を使って説明していきます。
図の左側に質量Mの地球があって、
このマーク（||）は距離がたくさん離れているという記号だと思ってください。
それで、スモールｍの物体。
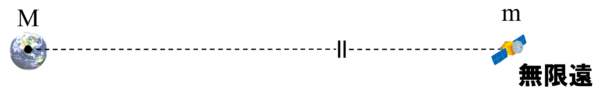この場所を無限遠とします。これで考えてみます。
ここでもう一度、位置エネルギーのことを考えてみます。
ｍｇに逆らってｈだけグぅ～っと持ち上げる。だから能力を持ちました。私が仕事をした分だけ能力になったんだという話をしました。
ということは、私たちが万有引力に逆らってどれだけ仕事をしたかってことを考えれば、それは位置エネルギーになるということです。
そこで、基準がはるか無限遠だということがわかってるので、はるか無限遠から距離ｒだけ離れたところまで質量ｍの物体を
よいしょ、よいしょ、よいしょ
と運ぶことを考えます。
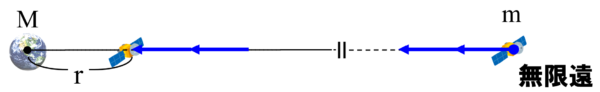
要するに、質量ｍの物体をもって、地球からの距離ｒまで運んだときに、どのくらいしんどかったのか…？
重力ｍｇに逆らって、グぅ～っとｈだけ持ち上げた…。あぁ、しんどかった…。けど、このボールがｍｇｈという位置エネルギーを持ってくれた…。こういう考え方です。
それでは行きます。
質量ｍの物体を無限遠の位置で持って、よっこい、よいしょって持って行ったんですか？？
それとも、これを持って「おぉ～っっ」て引きずられたんですか？
どっちでしょうか？
わかりますよね。
地球と物体は、万有引力で引き合っています。ということは、
私は、おぉ～、おっ、おぉっって地球の引力に引かれて仕事をされたんです。
したのではないです。これを考えても負であることがわかります。
つまり、この青い線に沿って、よいしょ、よいしょ、よいしょって、持っていくときに必要な仕事は負になります。私たちがしなければいけない仕事が負なんです。ということは、最終的に地球からの距離ｒの位置で持つ能力は、仕事をするための能力として使ってしまったから負にならなければいけません。
これがマイナスの意味です。
わかってもらえたでしょうか･･･？？
第2宇宙速度の計算
それでは今回の講義の最後になりますが、大切な話です。
これから、ある速度を簡単に求めてみたいと思います。
求めると言っても、式をさっと書くだけです。そういう風に思ってください。
今、ここに地球があります。
半径がRの地球です。
この地球の表面から、どぉ～んとロケットを速さｖで発射させます。
そして、
はるか無限遠でこのロケットが止まる時のｖを求めなさい！
と言われたとします。
簡単なことです。エネルギー保存です。
ボールをもってぼぉ～んと上へ投げました。
どこで止まりますか？
高さｈのところで止まる時には、どれくらいの速さで投げ出されますか？
どこで止まりましたか？
みんなエネルギー保存です。
それでは、これでやってみましょう。
地表面での、運動エネルギーと位置エネルギー。
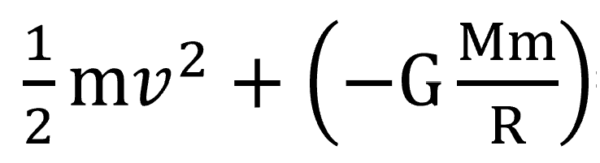
無限遠でのエネルギーは、無限遠で止まったんですから、運動エネルギーは０です。位置エネルギーは、基準点だから０です。
これで終わりです。
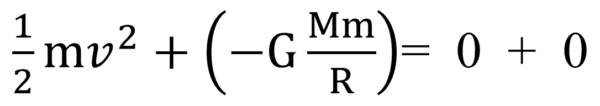
これでｖが求まります。これを第２宇宙速度と言うんです。また、問題解説の時にもやると思います。
しかし、何故ここでこんなことをやったのか？？
数式を和訳してみると
運動エネルギーと位置エネルギーのトータルが０なら無限遠に行ける！
と書いてあります。
もう一度言います。
地球を出発する時の運動エネルギーと位置エネルギーのトータルが、つまり力学的エネルギーのトータルが０なら無限遠まで行ける。
これでOKです。
これが、なかなか理解できないという人がいるので、もう少し説明します。簡単なことです。
地球というのは、ものすごく大きな負の位置エネルギーを持っているので、０にするためには、おぉ～きな正の運動エネルギーを与えてください…。
これなら理解できるでしょう。
最初に持ってる力学的エネルギーがぜ～んぶ０だったらいい！
っていうのは、よくわかりにくい。
力学的エネルギー０だったら、動かないんじゃないですか！？
とか、つい思ってしまいそうです。
でも違うんです。
そうじゃないんです。
もともと、ものすごく大きな負なんです。そのために、大きな運動エネルギーを与えてあげないと、はるか無限遠まで行ってくれませんよ！
そういう和訳になるんです。
実際に人工衛星を打ち上げる時に、こんなことが起きたら大変なことです。
２度と帰ってこれないというわけですから。それは大変なことになりますが、そういう実際の話とは違って、こういう式を立てなければいけない時が、入試問題では出てきます。その時に、和訳できない式を立ててはいけません。和訳できる式を立てられるから、どんな時にどんな意味の式を立てなければいけないかが見えてくるんです。
だから、入試問題を何問も何問も解いて、それで分かるものではないんです。
なぜ、この位置エネルギーが負なのか？
とか、そういうことを真剣に考えていく。
そして、私たちがよく知っているｍｇｈという位置エネルギー、そういうところから、だんだんとだんだんと難しいところへ持っていく…
そういう能力を皆さんが身につけると、もしも、難しい入試問題が出題されたとしても、
もしもこれがこうだったら、こうなるはずだ。
それがちょっとこうなってるだけだから、こういう風に出来る！！
そうすると、どんどんどんどん自分の領域に持っていけます。今回は、講義の中でケプラーの法則と万有引力というものを取り扱いました。これを理解しないと問題演習が無駄になってしまいますから、まずはここをしっかりと理解してください。
