目次
はじめに
今回は、万有引力の世界というものを取扱っていきます。5つ目の主題で円運動について行いましたが、その時に、ニュートンはアリストテレスと違って、

地上界も天上界も同じなんだと、りんごが落ちるように月もおちるんだ!
というような、とても画期的な考察に辿り着き、そして円運動を解析していったわけですねぇ。

この円運動が解析できたという事は、天空の世界、つまり天体についても同じような式が成立することに他ならないということです。
ニュートンが作った運動方程式ma=Fというのは、

地上界だけで成り立つものではない。りんごに対して成り立つものではなくて、月に対してもなりたつものである…
というような考え方を持つようになりました。
アリストテレスの物理学は約2000年間、科学的真実であるとして支持されてきたわけですが、それが1600年代になってから覆されることになります。2000年間、真実であると考えられていたことが覆されたわけですから、まさに画期的なことだった言えます。

今回は、天体の運動に話を絞って講義を進めて行くわけですが、天体の話をするにあたっては、ニュートン以外にも重要なケプラーという人についての話をしないといけません。

そのケプラーの前に、これは高校の教科書に少しだけ掲載されるようなことですが、この時代にティコ・ブラーエという人がいました。
この人は、簡単に言ってしまえば、天文学者ということなんですが、当時は、天文学という分野が正式にはなかった時代です。確かに天動説や地動説という考え方はありました。
しかし、天体を観測するというのは見たままを記録することが主流となってましたから、空を見上げて観察したものは、地球を中心として回っているように見えるわけです。ですから当時は、いろいろと誤った考え方が存在しました。

ティコ・ブラーエという人は、長年に渡って天体を観測していました。
そして、星々の運行状態がどのような状態にあったかを書き留めていく。そういう仕事をしていました。一説によると、王室お抱えの占い師であったと…、

今で言うと星占いのおじさんですか…??
彼は天空に対して常に神聖な気持ちをもっていて、観測する時には、いつも正装でちゃんとした服を着て観測していたと言われています。

ティコ・ブラーエが活躍した時代には、望遠鏡は存在しておりません。
全て肉眼で観察することになったわけですが、そこにケプラーが弟子として入ってきました。そして、ケプラーはティコ・ブラーエの下で1年間弟子としてはたらくことになります。なぜたったの1年間かというと、ケプラーが入門してから約1年後に、ティコ・ブラーエが亡くなるんです。

ティコ・ブラーエは、膨大なデータを残して亡くなることになるのですが、実は、それを受け継いだのがケプラーです。
一説には、ティコ・ブラーエの両親に懇願して、そのデータを譲ってもらったという説もあれば、盗み出したという説もあるわけですが、ずいぶん昔の話ですので、どちらが真実かはわかりません。
いずれにせよ、ケプラーは膨大なデータを手にすることになります。これが、天体の分野においてはラッキーだったのかもしれません。

ティコ・ブラーエという人は、天体の精密な測定を行い膨大なデータを残すわけですが、ケプラーは、この膨大なデータを分析しようとしたんです。
そして、何か成り立つ法則のようなものがないだろうかと考えました。

ただのデータを学問へと持ち込んだと言っても過言ではないでしょう。
ケプラーはそういう人だったんです。

そのような歴史的背景から、ケプラーは情報処理の祖とも言われています。
例えば、我々は平均をとるというようなことをやります。5つのデータがあったときに、そのデータを全部足して5で割るというようなことをやりますね。ケプラーはティコの膨大なデータを前に、そういう風なことを行い、より正しい値というか、より妥当性のある数値を求めようとしたと言われています。

ただ単にデータの処理を行ったのではなく、その中から、重要な法則をいろいろと見つけ出していきました。
それで、その法則が本当に正しいのかどうかという所を、ニュートンが月の運動を利用して実際に確かめていったところ、

どうも正しい…
そうなってくると、

そういう風な運動をするということは、きっと何か力が働いてなければならない…
と、そのような学問的な流れがあったわけです。
皆さんは、この2人以外にもガリレオ・ガリレイという有名な人をご存知だと思いますが、実はケプラーとガリレオ・ガリレイの間には親密な関係があって、文通もしていたという記録が残っています。もちろん、ガリレオ・ガリレイは、望遠鏡を発明した人ですから、望遠鏡を使って天体を観察していた人でもあるわけです。

今回は、その流れを追いかけながら、基礎的なところを学んでいきます。
主題6:万有引力の世界
それでは、主題の6番目になります。
それでは、万有引力の世界というものを取扱っていきます。
その中の1つ目の項目になるわけですが、ケプラーの法則について確認していきましょう。
①ケプラーの法則
先ほどにも説明した通り、

ケプラーという人は、膨大な実験観測データをもとに、どんな法則が成り立っているのかを見つけ出した!
と言いました。
現在では、高等数学を用いて理論的に成り立っていることが証明されているものばかりです。

しかし、皆さんが高校生の間はケプラーと同じ立場をとってください。
すなわち、実験データから導かれた法則であるという風な考え方をしてもらいます。ですから、ケプラーの法則には3つの法則があるわけですが、その3つの法則を覚えてもらいます。これらは観測したことによってわかったことである。後に、それが高等数学を用いて証明されることになるんですが、それは今はお預けです。

それでは今から星々の運行について、どのような法則を見つけたのかを確認していきますが、今も言ったように実験観測から出てきたものであるととらえないといけません。

最終的に覚えなければいけないわけです。
そういった時に、あまりダラダラダラダラと長い説明をすると忘れてしまいます。だから、教科書では丁寧に説明されているわけですけども、それらを簡潔にまとめて、

こういう事さえわかっていれば大丈夫!
ということを説明していきます。
第1法則:だ円軌道の法則
では行きます。第1法則です。古代ギリシャ時代から天空を見上げて、星々は円運動をしていると考えられてきました。


しかし、ケプラーはそれがうまくいかない。円運動ではうまく説明できない!
という事を見つけ出します。

まず1つ目の法則が、楕円軌道であると…。
要は、
完全な円にはなっていない…
ということですね。
ある星の運行状態を調べてみる、時間と共にプロットしていく…、
そうすると地球を中心に円を描けたりします。地球でいうと太陽を中心に円が描けるということになるわけですが、

合わないんですねぇ…。
ぴったりと円として合わない。

角度にして8分!
分というのは角度の単位です。1度の60分の1が1分。そのくらいのずれがありました。
我々にすれば1度も違っていないわけですから、

そんなの誤差だろ!?
と捉えてしまいがちなんですが、

実はケプラーはティコ・ブラーエという人が、どんな人かってことが良くわかっていました。
とても神経質な人だった。
あのティコ・ブラーエという人が、角度にして8分も間違えるわけがない!
と、そういう捉え方をして、

円軌道ではない…
と考えていきました。ケプラーは、実は、いろいろな軌道を考えていたみたいです。
双曲線の上に乗っかってるのではないか??
それとも放物線の上に乗っかってるのではないか??
と、いろいろ考えていったようです。

そして、最終的に行き着いたのが楕円軌道である…
という訳です。
第2法則:面積速度一定の法則
それでは次に行きます。

面積速度が一定である…。これは、少し説明をしないといけません。
なんのことやら良くわからないのですが、その説明は後にします。
第3法則:調和の法則
次に3番目ですが、実は第1法則と第2法則は同時に発表されるのですが、それから随分経ってから、この第3法則というのが発表されることになります。
![]()
周期の2乗は長半径の3乗に比例する。kは比例定数です。


このくらいだったら覚えられますよね。
いずれも非常に大切な事です。
1番の楕円軌道であるというところは何も問題ないでしょう。しかし、2番や3番については説明をしていかないといけません。
面積速度一定の法則について

まず、大事なのが面積速度というものです。
この面積速度というのは、絵で描いてしまうとそれほど難しいものではないんです。

ただ文章にすると非常にわかりにくいんですねぇ…。
だから、教科書にも丁寧に書いてあるんですけども、結局何なのかってところがわかりにくいところですから、少し説明をしていきます。
楕円の一部でもなんでもいいんですが…
例えば、ここに地球があるとしましょう。
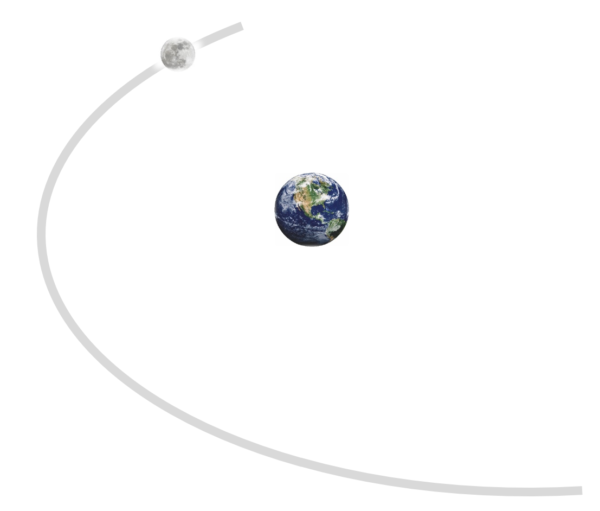
そして、月が、こういう風な軌道をとっている。

それで…、実は、面白い現象が起きるんです。

もちろん、ケプラーが気付いたんですよ。
ある一定の時間で、この星の運動を書いてみると、ちょっと奇妙な事が起きるんです。

それは何か…??
例えば、ある時間に星(図では月)がここにあったと、そして、またある時間、例えば1時間後とか2時間ごとか、きまった時間間隔でプロットしてみるんです。
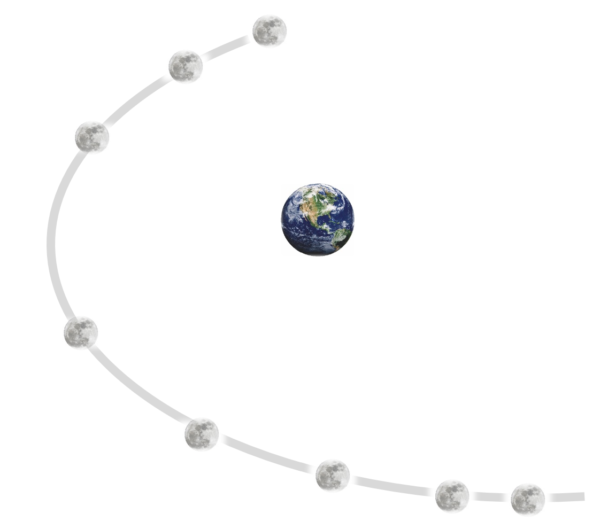

なんだって感じがしますね。
ケプラーもそう思ったんですよ。それで、その時に面積速度一定っていうのは、何なのかって言うと…、
どこでもいいのですが。隣り合う星の2点と地球を結んだ部分を2か所取り出します。
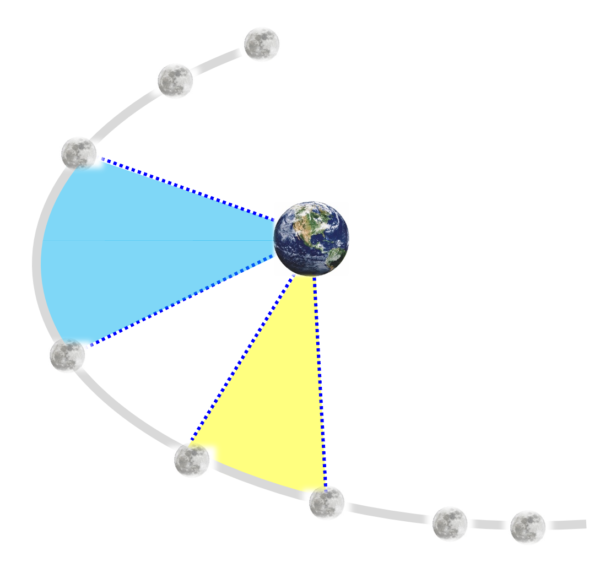

この時、この2か所の面積が同じだって言ってるんです。

そういう動きをしていますよ
って言ってるんですねぇ。これが面積速度一定の法則。
図の青い部分の面積をS1として、黄色い部分の面積をS2とした時に面積速度一定というのはS1とS2が等しいんです。
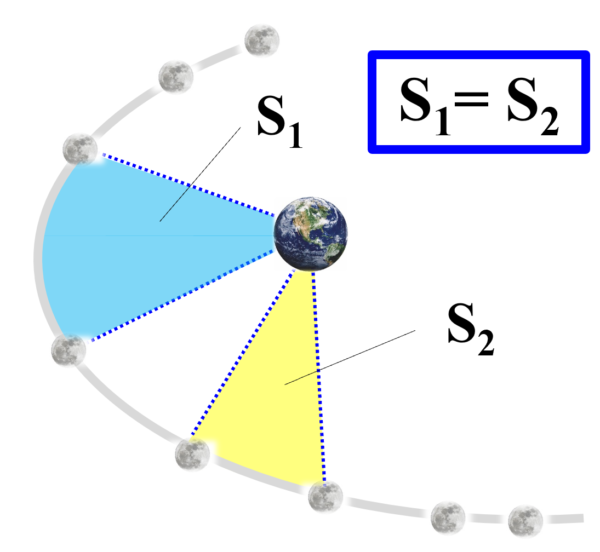
ケプラーは、惑星が面積速度が一定になるような運動をしているということを見つけ出したんです。

実はこれに似た現象を皆さんも知ってますよ。
たぶんですけど…。
この絵を見てもわかるように、ここが中心なわけですよねぇ、近場を通る時には、速くて、遠くにいくと遅いということがわかります。
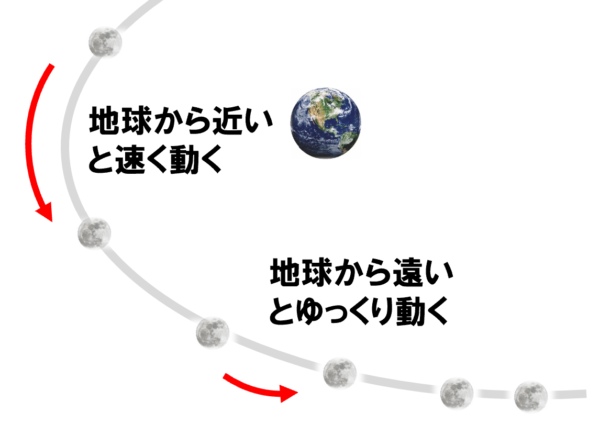
これが成り立つためには。すぐ近くを通るところは「びゅ~ん」っと速くて、遠くに行くと遅くなるわけですね。そういうことが、これから容易に想像できるということです。

この辺まで説明すると…

まだ、この辺じゃ気付かないかなぁ…
例えば、こういう楕円軌道があったとします。
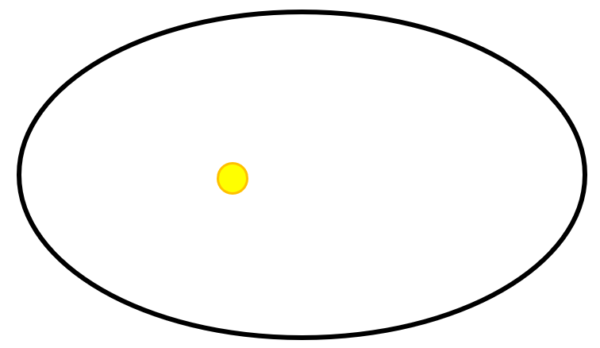
黄色い●が1つの焦点です。この軌道上をグルグルグルグル回っていると…。
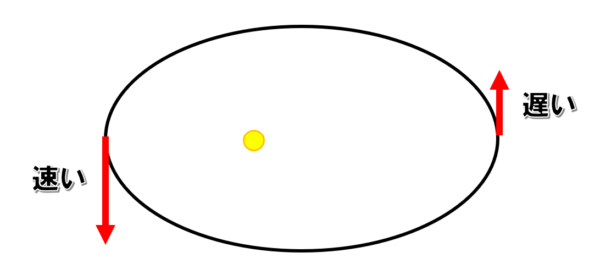
そうした時に、左側を通過する時の速さと、右側を通過する時の速さでは、こっち側を通過する時の方が遅いですよね。

何で??

だ円軌道を周回する物体の速度ベクトルと焦点で形成される三角形の面積に近似することが多いのですが…
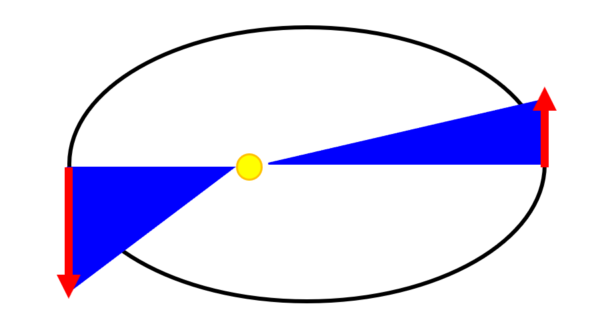
上の図の2つの三角形の面積です。

ケプラーの第2法則によると2つの三角形の面積は同じでなければならないんです。
だから近くになると早くて遠くになると遅いわけです。

ここまで理解して頂ければ、もう一言いえばわかりますよ。

皆さんは、フィギュアスケートって見たことありますか?
フィギュアスケートでよくやる終わりの時にくるくるくる~と回転して、音楽が終わると同時にピタぁっと止まって最後のポーズを決めるという選手が多いですよね。


そういうの見たことないですか?
あれは、最初からすごい速度で回っていないですよね。最初、スゥ~っとゆっくり回り始めておきながら最後にグルグルグルグルグルっと回ってピタぁっと止まりますよね。

あれだけで何で早くなるんですか??
途中で氷の面を選手は蹴ってないですよ。手とかを広げた状態でグルグルっと回り始めるわけです。手とかを広げた状態で、グゥッと回り始めるわけです。それを、だんだん自分の胴体の方に手を近づけてくるわけです。

そうすると、だんだん半径が小さくなってくるから速くなるんです。

わかってもらえるかなぁ…。

あれも面積速度一定なんですよ。
だから身体で無理をして加速しているのではなくて、広げた状態から、ぎゅ~っと縮めると、速くなっちゃうんです。

現在では角運動量保存則ということで証明されていますが、皆さんは現象の方からそういうものをとらえていただきたい。
という風に思います。
私についてももちろんそうですが、今はケプラーが発見したものを皆さんに伝えてるだけで、受け売りをしているだけなんですけど、これに気付くっていうことは凄いことですよね。
普通の人だったら、こういう風にプロットして行って、

こんなになってるんだぁ…ふ~ん。
となって終わりそうなんですけども、
ところが、
ここの面積を考えて…
っていう、そういう考え方というか発想はすごいですね。


実際にここの面積を求めるっていうのは難しいんです。
円ではありませんから…、
ですから、ケプラーは、これを小さな三角形に分割していきながら、どぉ~っと足していくようなこともやっていました。
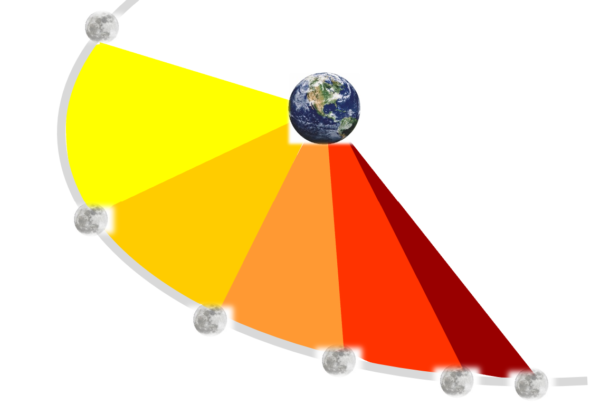

実は、これがニュートンの積分の発見にもつながっていることなんですねぇ。
小さく分割をしていって面積を求める…、というような。ですから、ケプラーがやった仕事っていうのは、非常に大きな業績なんです。
これがケプラーの第2法則、面積速度一定の法則です。
そして、もう一つ説明しなければならないものがあります。それがケプラーの第3法則です。Tの2乗がrの3乗に比例をする。

言ってみれば、周期の2乗が長半径の3乗に比例する。
長半径というのは、楕円があった時の長い方の半分のことです。長い方の半分です。
これはただの実験事実としてとらえてもいいんです。それでもいいんですが、ケプラーの第3法則は、少し大事なことと結びついているので、次の項目で話をすることにします。