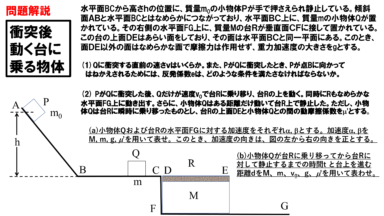
はじめに
前回の円運動の問題演習に引き続き、もう一題だけ円運動に関わる問題を解説します。
■前回の解説問題
今回の問題は、重要問題集４７番の鉛直面内の円運動の問題です。
この前の円錐振り子の問題では、
円運動は円の中心方向に落ち込む運動である…
という所から、運動方程式へと力の関係式に持ち込んでいきました。
今回の問題は、円運動が関わってくるであろうことは図を見ればわかりますが、すぐさま力の関係式へ持ち込もうとすると思うように解けません。そういったところを確認しながら問題の解説に入っていきます。
※問題文を掲載すると著作権に抵触するため、重要問題集をお持ちでない方は書店等でお買い求めください。
重要問題集４７番の鉛直面内の円運動
（１）解説
これは運動量保存の問題演習でも同じようなことをやりましたねぇ。
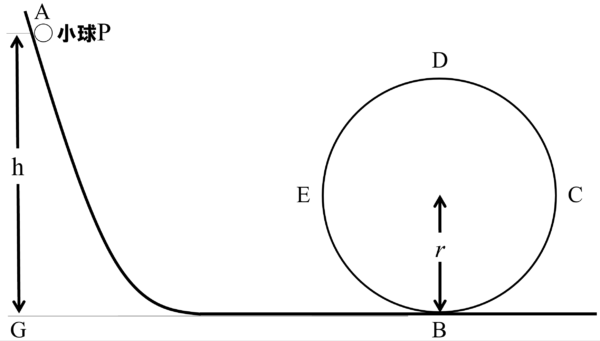
水平面GBから高さｈにあるところから小球Pを転がしたんです。この時、小球は、ｍｇという重力を受けながら高さにしてｈに相当する距離だけ移動したのですから、点Bを通過する時の小球Pの速さvBは、力の距離的効果、つまり力学的エネルギー保存則を使って求めます。
よって、
となります。
（２）解説
次に（２）～（４）について、ｍ、ｇ、ｈ、ｒのうち必要な記号を用いて答えよ。
それでは、（２）番と（３）番を一緒に見ていきます。
（２）ループの最高点Dにおける小球Pの速さvDを求めよ。
（３）点Dにおいて、小球Pがレールから受ける垂直抗力の大きさNDを求めよ。
さて、それでは、（２）番から見ていきます。
この問題はエネルギー保存則で解きます。何故だかわかりますか…??
（１）番がエネルギー保存則だったから…？
それは理由としては弱いですねぇ…
もしも、（２）番から突然問題が始まっていたらどうですか…？？
これは、大問題ですねぇ…
とりあえず解いてみましょう。
点Aから離れた小球Pは点Dまでやってきます。点Dを通過して運動しないといけませんから点AはDよりも高くないといけませんし、点Dで小球Pは速さを持っていないといけません。
点Aから下ってきた小球Pは、Bの位置から重力ｍｇに逆らって２ｒの高さある点Dまでやってきたわけです。したがって、力の距離的効果、エネルギー保存則です。
よって点Dでの速さをvDとすると、力学的エネルギーの保存則から、
となります。
さぁ、これでvD が求まりました。重力ｍｇによって点Aから下ってきた小物体Pが、今度は重力に逆らって点Dまでやってきた。そこで、力学的エネルギー保存則によってvDを求めたわけですが…、
これ円運動ですよねぇ…
円運動であれば加速度は
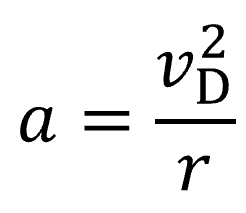と書けるじゃないですか？
今回の問題であれば、vDを求めたいんですよねぇ。加速度a を求めたら、vD が出るじゃないですか…?? それなら、運動方程式で解けばいいじゃないですか？
しかし、運動方程式では解いていません。
なぜですか？
そういわれると難しいです。
物理の大切なところです。
それでは説明します。
まず、速さを求めたかった。
その時、等速円運動の速さの式はダメです。速さが一定ではないですから。したがって、エネルギー保存則というのが候補の一つとして挙がります。
運動量保存則はダメですよ。時間は関係ありませんから。
しかし、もう一個、円運動では加速度が特別な表記を持っていますから、加速度を求める方法で、速度とか速さが出てくるはずなんです。
でも、この問題は使わないんです。なぜか??
こう聞いているわけです。
結論からいきます。
床からの抗力がわからないからです。
運動方程式を立てるためには、すべての力が必要です。
しかし、レールと小球Pがどれくらいの力で接触しているのかが、今のところわからないからです。
さぁ皆さん。もう一度問題に戻ってみます。
（２）ループの最高点Dにおける小球Pの速さvDを求めよ。
（３）点Dにおいて、小球Pがレールから受ける垂直抗力の大きさNDを求めよ。
（２）の段階で、レールからの抗力の大きさがわかっていません。抗力の大きさがわかっていない段階では、（２）で力の関係式を使ってはいけないということになります。だから、力の関係式を使うのではなくて、力の距離的効果（力学的エネルギー保存則）へ持っていった。
なるほど。
（３）の問題を解いたらいっしょにまとめていきます。大事なところですから。
（３）解説
それでは、
（３）点Dにおいて垂直抗力の大きさNDを求めよ！
という問題です。
力を求めよということですから、運動方程式に持っていこう！
ということです。
ちょっとやってみましょう。
点Dにおいては、vDという速さを持ってます。そして下向きに重力ｍｇを持っていますね。接触力としてレールから受ける垂直抗力NDがある。
このNDを求めるんです。
円運動ですから、円の中心方向に加速度a 。
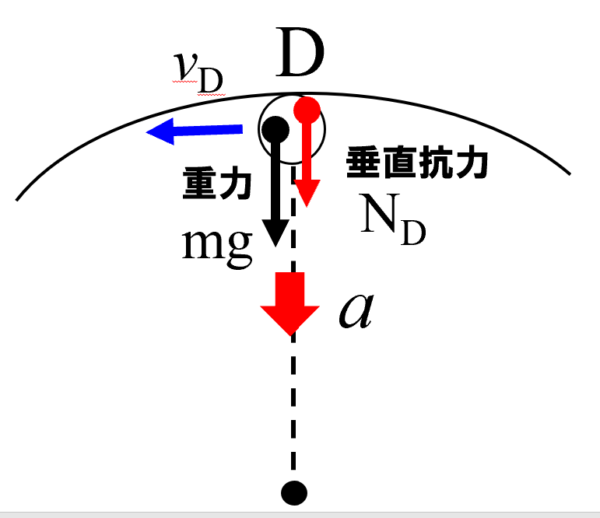
遠心力を乱用してはダメですよ。
運動方程式より、質量ｍの物体に加速度a を乗じさせたのは誰ですか？
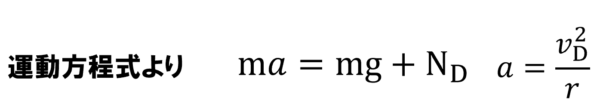
ここで加速度aはvD２/ｒと書けるので、（２）で求めたvDを使うと答えはこうなります。
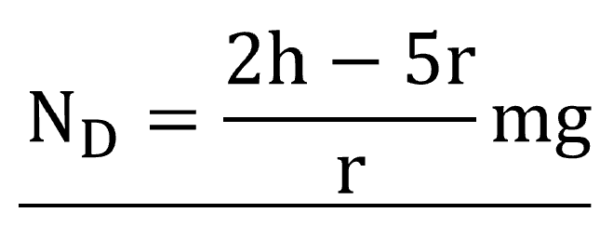
さぁそれでは、解説を続けていきます。大事なところです。
今、流れとして（１）でエネルギー保存則を使いながら vDを求めました。vDを求めると円運動の半径はわかっていますから、加速度が求まったことになります。
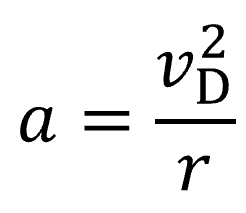
加速度がわかった為に、運動方程式が立てられるようになります。そのおかげでNDがわかったわけです。
言ってみれば、連立しているんですねぇ。
ここのvD2と
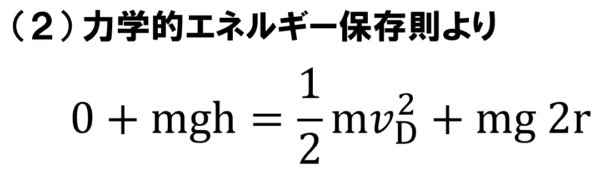
（２）のvD2を連立していることになります。
こういう風な重力に逆らった形での鉛直面内の円運動では、速さを求めるという事には２つの方法があるんです。
いずれもvという表記があるからですね。
しかし、本問では（２）で速さvを求め（３）で垂直抗力を求めよと言われた。
ということは（３）で力の関係式を使わないといけないんです。だったら（３）でどうしても運動方程式を使いたいんです。ということは（２）の速さを求めるのは（運動方程式ではなく）エネルギー保存です。
エネルギー保存則からvDを求め、vDを円運動の加速度の式に代入し、運動方程式から垂直抗力NDを求める。
これでうまく行きます。
という風に考えないと、物理は強くなりません。
どこから問題を問われるかわかりませんから。
私が皆さんに対して心配していることと言うのは、例えばこれと全く同じ問題が出たとします。これと同じ問題です。全く同じ問題が出たんだけども、（２）がない時です。（３）が突然２番目の問題に出て来て、
垂直抗力NDを求めなさい
と来たら…、
その時に自分でエネルギー保存則を立てられますか？
ちゃんと。間を飛ばされても立てられますか？
こういうことが頭に入っていると、垂直抗力を求めなさいと言われたら、
あれっ、vDがいるじゃん。vDがわからないと垂直抗力が出てこねぇじゃん。なんだ、別の方法でvD求めなきゃ!!
あぁ~!! 重力に逆らって上に上がったんだ。だからエネルギー保存だ！！
（２）番をヒントに（３）番を解いたんじゃないんです。
（３）番がいきなり出されても出来るんです。
なぜならば、私たちは v というものの表記がエネルギーのなかにあったり、加速度のなかにあったりするから、エネルギー保存則や運動方程式であるという理由が分かったうえで解法を探しているんです。
この問題と似たようなのを解いたからできるんじゃないんです。
そうやって理由がわかることによって解法を見つけているという事は、変な問われ方したり、見たことない設定にされていたとしても、
と、
それならエネルギー保存と運動方程式しか考え方はない。
どちらかの問題でどちらかの解法を使い、残りの問題でもう片方を使えば必ず解けるというわけです。今回は垂直抗力を求めるために運動方程式を使い速さを求めるためエネルギー保存則を使ったわけです。
ここは大切なところですが覚えるんじゃなくて、ちゃんと理解することが大事です。
こういうところをきちんと理解できると、次へ次へと繋がっていくわけですねぇ。まずは、速度の表記を知る。そして、円の中心方向に落ち込ませるということ。大切なところですから、しっかりと理解してください。
