目次
はじめに
今回は実際に運動量にまつわる問題を解説していきます。

しかし、これから受験を迎える高校生の立場からすると、重要問題集を買ったはいいが、

という状況がままあるように思います。
私自身、公立高校に勤務して物理を教えていた経験があるわけですが、
先生側の立場からすると、

という事情があります。

って話なのですが、
多くの現役受験生の場合、まずは大学入試センター試験を突破することが最優先ですから、大学個別の入試問題に着手するのは、受験シーズンの終盤にさしかかってきます。
そうしますと、授業日数の関係から、

という結果になってしまいます。
そのような背景を踏まえて、全てではないですが問題解説を行っていきますので、是非この問題集を有効に活用していただければと思います。
40:衝突後動く台に乗る物体の問題(1)
↑この動画では、問題設定の確認から(1)の解説まで行っております。
早速問題に移っていきますが、今回取り扱う問題は、数研出版『2020実践重要問題集』の40の衝突後動く台に乗る物体の問題です。
※最新の物理重要問題集には該当の問題は取り扱われなくなったので、当ブログにおいて掲載します。
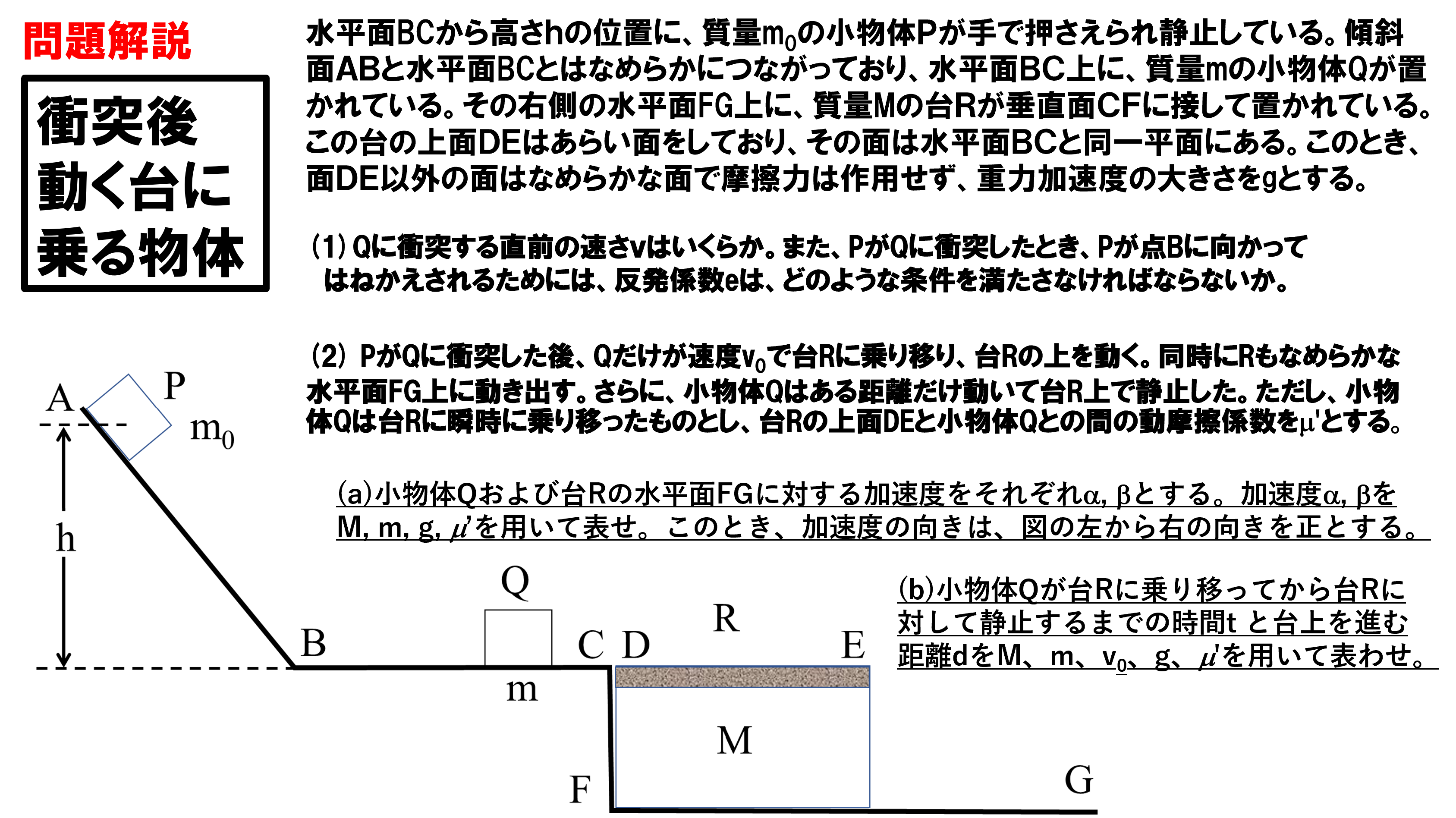
問題設定の図

BCから高さhにあるAから、質量m0の物体Pがすべり落ちるわけですね。
その先には、物体Qがありますから、ここで衝突が起こります。

それから物体Qが台Rに乗り移る。この台の上面は粗い面で、それ以外はなめらかな面であるということですから、物体Qが台R上を動きながら、台RはFG上をすべり始めることになります。

さて、これから問題の解説に移っていきます。

しかし、皆さんが入試問題を実際に解くときには、「衝突後動く台に乗る物体」などというタイトルはありません。
おそらく第5問とか、第4問とか、大問番号がふられていて、長い問題文が載っているわけですね。
したがって、これから問題解説を聞くときは、運動量保存だけにかかわらず、
「なぜこの解法なのか?」という必然性を見いだすための訓練を行っている!
という意識を持っていてください。
(1)解答・解説
それではいきます。(1)番。
(1)番は、問題が2つに別れています。

それでは、前半部分の物体pの速さvを求めるところから順番にやっていきましょう。
物体Pは高さhある斜面ABを下って、水平面BC上にある物体Qに向かうわけですね。

したがって、水平面BCを高さの基準にとれば、1/2m0v2=m0gh と書けます。


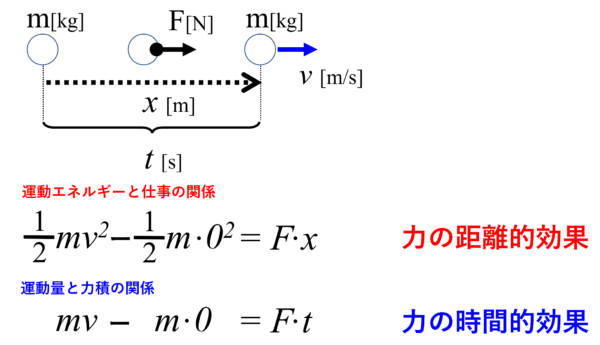
これは、力の距離的効果。仕事と運動エネルギーの関係です。
40:衝突後動く台に乗る物体の問題(2)
↑この動画において、(2)の解説および「運動方程式と等加速度運動の式」の関わりから、最適な解法を選択するための考え方について学びます。
大学入試問題においては、当然のことながら、問題集で解いたものと全く同じ内容のものが出題されることはありません。似たような問題が出題されることはあるにしても、設問の内容が変わるだけでも、問題の難易度が様変わりします。
そのような変化に対して、

なぜこの解法が有効なのか?
と言ったことを確認していきます。
(2)解答・解説
それでは、(2)の問題に移りましょう。

(a)小物体Qおよび台Rの水平面FGに対する加速度をそれぞれa, bとする。加速度a, bをM, m, g, m’を用いて表せ。このとき、加速度の向きは、図の左から右の向きを正とする。
小物体Qが台Rに乗り移った後、小物体Qと台Rには摩擦力が働きます。そのために、物体Qは減速しながら台R上を動きます。一方台Rについては右向きの摩擦力を受けることで加速して水平面FG上を動き出すというわけですね。

そして、小物体Qは台R上で静止した…

それでは解答に移ります。

ということは摩擦力と加速度α、βの因果関係を考えれば言い訳ですから運動方程式を立てれば良いですよね。
ここまで方針がはっきりすればあとは式を立てれば良いだけですが、その前に物体Qと台Rに働く力を確認しておきます。
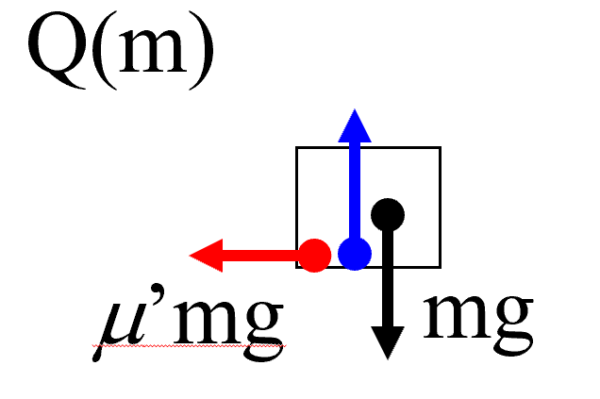
質量mの小物体Qに働く力は地球からの引力である重力mgとその重力を支えるように床からの垂直抗力です。
そして、台Rは粗い面ですので右向きに進む物体Qの進行を妨げるように、動摩擦力m'mgが働きます。

というわけですね。
したがって、小物体Qに働く力は以上の3つとなります。
そして、次に台Rです。
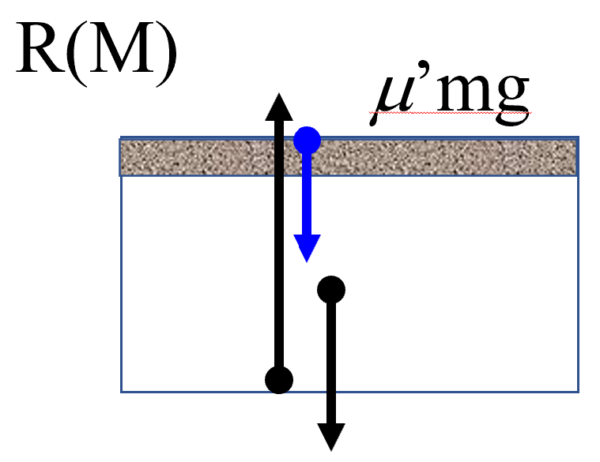
まずは重力Mgそして、上に小物体Qが乗っかっているからその質量に相当する力(図の青矢印)が加わりますね。そして、この2つを支えるように水平面FGからの垂直抗力が働きます。このままだと台Rは3つの力がつり合って静止しているだけになりますが、実際には、右向きに動き出した訳ですね。

ここで大切になってくるのが、ニュートンの運動の第3法則、作用反作用の法則です。
接触力には同じ大きさで互いに逆向きの力が対になって働いている。
というのが作用反作用の法則ですから、小物体Qと台Rに関する接触力を確認していくと…
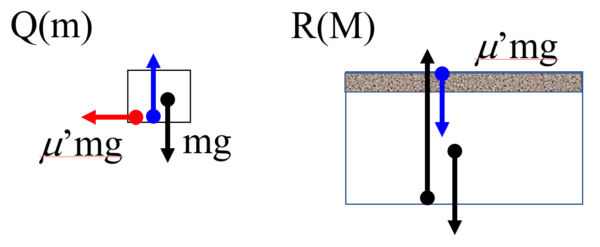
図の2本の青い矢印、これが作用反作用の法則をまず満たしていますね。次に赤い矢印を見てみると、小物体Qには左向きに働いていますが、台Rにはペアになる力が抜けていますね。
だから、台Rには右向きに動摩擦力m'mgが働きます。


というわけですから、加速度の方向に関わる力を見てみると、確かにそれぞれの物体に働く動摩擦力がその原因であると考えて良さそうですね。
それでは実際に運動方程式を立てていきます。右向きを正とします。



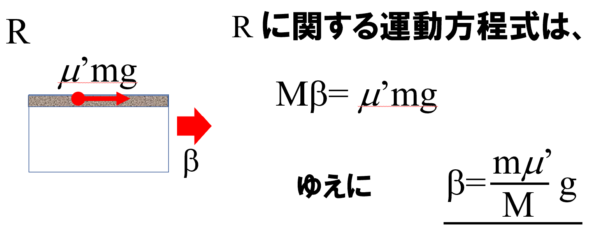
これで良いわけです。それぞれを解いてやれば解答がα、βが求まります。

それでは、次に行きます(b)です。
(b)小物体Qが台Rに乗り移ってから台Rに対して静止するまでの時間t と台上を進む距離dをM、m、v0、g、m'を用いて表わせ。
(a)の問題において加速度α、βを求めました。加速度αの-m'g、加速度βのM分のm'mgについては定数である質量m、M、動摩擦係数m'、そして重力加速度gで表されていていずれも定数によって示されているので、加速度α、βも定数になります。
したがって、

ということですね。
そこでまずは、時間t から考えていきます。
求める時間は小物体Qが台Rに対して静止するまでの時間ですから、まず小物体が台Rの上に初速度v0で乗り移ってから、台Rに対して静止するまでの間ですね。小物体Qが台Rに乗り移ると動摩擦力が働きますから小物体Qは減速します。そして、台Rは右向きの摩擦力が働いているので動き始めます(加速する)。

そして、台Rについては滑らかな水平面FG上にあるのでその時の速度を維持して滑り続けることになる。したがって、外から見ると小物体Qは台Rと同じ速度で移動することになります(小物体Q、台Rは等速直線運動する)。
だから、

と言い換えることができますね。
次に距離dについてですが、よくこういうミスをする生徒がいます。


って言うんですねぇ…

dは台上を進む距離です。先ほど数式で求めた距離は床に対して移動した距離なので、これはdではありません。

求めないといけない距離dは次の図に示す部分です。

床に対して小物体Q、台Rがそれぞれ進んだ距離をxQ, xRとするとxQからxRを差し引いた部分が距離dに相当します。入試問題を解く時は、問題文を流し読みせずにきちんと理解してから進めて下さい。
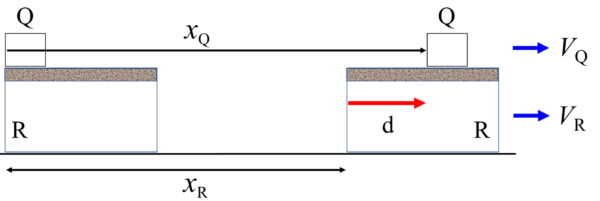
それではdを求めていきましょう。時刻tでの小物体Qと台Rの速度をVQ, VRとすると、等加速度運動の式より、
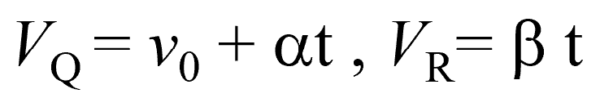
と書けます。
求めたい時間は VQ=VR となる時間ですから、2つの式をイコールで結びます。
よって時間tを求めてやると次のようになります。

次に小物体Qが台Rに対して進んだ距離dを求めていきますが、xQ とxRをそれぞれ求めると次のようになります。
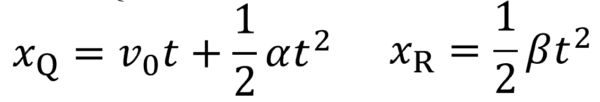
したがってxQ からxRを引いてdを求めてやると最終的にdはこうなります。

ここでは解答だけしか示していませんが、途中計算がやや複雑なので、計算ミスをしないように注意してください。
解法の必然性について
さあこれで40番の問題が全て解けたわけですが、これで終わりではありません。

この問題を解くのであればこれで十分ですが、皆さんはこの種の問題が解けないといけません。入試問題には全く同じ問題が出題されるわけではありませんから、

例えば今回の問題ですが、(2)の(a)は言ってしまえば(b)を解くためのヒントになっていたわけです。

頭の回転が速い人であれば、
物体に働く力をイメージして運動方程式を立てて、速度が等しくなる条件から時間tを求める。それから距離dを求める。
ということはできるかもしれません。
しかし、

とか

なんて

そうして試験時間だけが過ぎていくと、だんだん焦りが募っていって計算が雑になってくる。

なんてことがありますから、

そして
(a)のような問題がなく時間tや距離dを直接求めることが要求された時に、どのような手段をとるべきなのか!?
ということを吟味していく必要があります。

だから、この先の解説もよく聞いてください。

(a)は加速度を求めるという問題でした。そこで状況を確認した時に、加速度を生じさせる原因は動摩擦力であることが見えてきました。そこを切り口として運動方程式を立て、力と加速度の関係から加速度を求めました。
それから(b)の問題においては時間tと距離dを求めたいわけですが、物体が等加速度運動をすることから、まず速度に着目して速度と時間の関係式から時間を求め、そして時間と距離の関係式から距離を求めました。
もう一度整理すると最終的に時間であったり距離を求めるために等加速度運動の式を利用したい訳ですが、加速度の表記が分からないから力に着目して運動方程式から加速度を求めた。そして、求めた加速度から時間と距離を求めた。
ということです。したがって加速度というのは、運動方程式と等加速度運動の式を結びつけるいわば接着剤のような役割を果たしていたわけです。
そして、ここから考えてみたいのは(a)の問題がなくて、直接時間と距離を求めないといけない場合です。
これはあえて言い換えると、

ということです。
それでは実際にやっていきます。
(2)の問題に入った段階で、まず何を行ったのかというと、小物体Qと台Rに働く力を考えました。力の図を書いてみたところ、

と判断したわけですね。
そして速度が等しくなるという条件から時間tを求め、時間tの間に進んだ距離の関係からdを求めた。速度は時間tでは等しくなるということなので、VQ, VRではなくここではV としておきます。
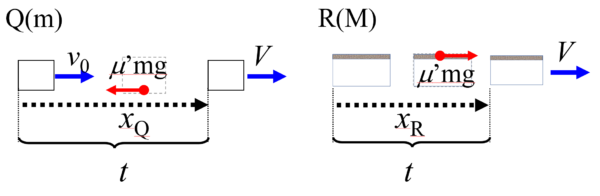
さて、みなさんこの図どこかで見ましたねぇ。

台Rも同じですねぇ。

そして、

もう大丈夫ですね。力の時間的効果(仕事と力積の関係)、力の距離的効果(仕事と運動エネルギーの関係)です。
※詳しくは次の記事を参照してください。
さあ、それではやってみましょう。
まずは力の時間的効果、運動量と力積の関係です。

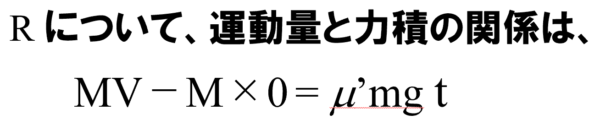
できましたねぇ。
この式を連立してとけばtを求められますね。まずは2式の和をとってみましょうか。

後でVイコールという式にしたいので、マイナスを右辺に持って行きました。
そうすると…

和訳してみると、
と書いてある。

これ運動量保存則の式ですねぇ。公式を丸暗記しなくても勝手に出てきました。

なんて勉強はしなくても大丈夫ですよ。
よってVとtはこのようになります。

ここまで聞いて頂けたら、如何に基本的なことが大切かがわかってもらえると思います。私が話している内容は、全て教科書に書かれていることです。入試問題というとなんか難しいことをしないといけないと思うかもしれませんが、物理においてはそうではありません。

この問題を丸暗記しただけの人だったら、この種の問題でを求めなさいと言われたらまず加速度を求めるでしょう。
しかし、なぜ加速度を求めるのか!?
それは

というのであれば分かりますが、

なんていうのは本当の物理の実力ではありません。同種の問題であっても設問の内容によって難易度がぐっと変わりますし、そこで求められる解法も変化していきます。小物体Qに摩擦力がt秒間働いたから減速して速度がVになった。台Rには摩擦力がt秒間働いたから加速して速度がVになった。
それならば物理基礎だけでなく基礎無しの物理を学習した皆さんでしたら、敢えて求める必要のない加速度を計算しなくても、運動量と力積の関係から時間を求めればよいわけです。

さぁ、これで時間tに関する話が終わって距離dに映るのですが、

というのも今の話の流れに沿って、力の距離的効果を使ってもいいのですが、先程の回答と比べて計算量にさほど大きな差が出てきません。現時点で時間tをすでに求めたのであればあえて力の距離的効果に固執する必要はないでしょう。
しかし距離dについては、次の講義でお伝えする慣性力を利用するとまた違った解法が利用できます。今回の講義は、運動量の問題解法を主題としていることもありますので、この先の説明は次回に行うこととします。



















