徹底攻略！大学入試物理 円運動の基礎③（遠心力について）

遠心力について

■円運動に関する講義

遠心力という力について

 

 

え～何にしましょうか。遊園地にしましょうか。

遊園地というのは、限られた敷地の中で遊ぼうとするものですから、当然、グルグル回るものが多いんです。

 

 

要は、限られた空間の中で何か乗り物に乗るってことは、ぐるっと回って帰ってくるものを作るというのが常でしょう。だから、遠心力とかを体感することが出来るのは、遊園地が非常に多いと思いますが、遠心力というのは私たちの生活の中に入り込んでいる言葉なんです。

 

 

って言って分かりますか？？

 

 

例えば、電車に乗ります。そこで電車が発進します。

そして急ブレーキをキキキ～っとかけた。するとどうなりますか？？

 

 

それからガァ～って急に発信すると、おっとっとっとっとってなる。あれですよ。

 

 

だから、円運動の時には特別に遠心力と呼んでいるだけです。

 

 円運動する物体を眺める（慣性系）

では、今から円運動にまつわる力の関係式を見ていこうと思います。

 

まずですねぇ、さっきの例で行きましょう。

ロープの先に重りをつけてくるくるくるくる回してる。

それを天井の真上から見ている。

 

 

それでいきましょう。

その時に、ロープがあって、重りがある。ここが中心です。

速さv で回っている。

 

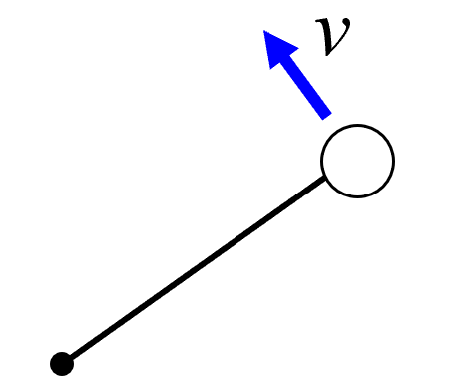
ちょっと変な絵になりますが、これが私です。観測者。

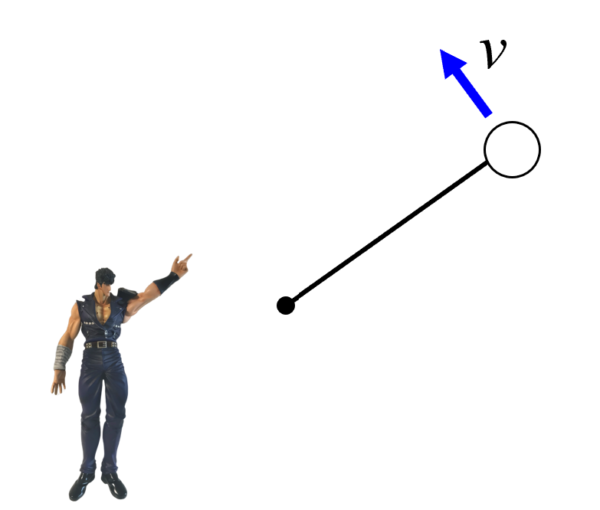
ボールがグルグルグルグル回っています。

 

 

 

 

 

 

 

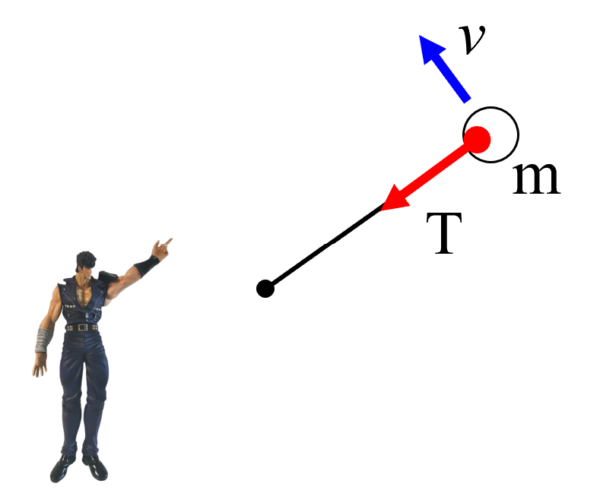
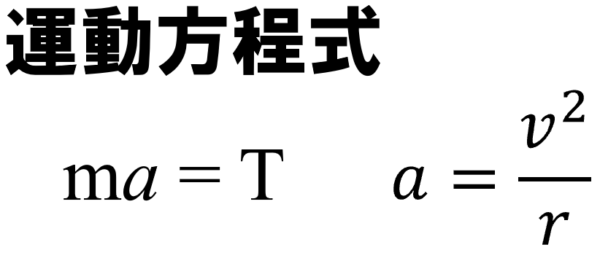
これが運動方程式です。ただし、円運動です。加速度は、特別に r 分のv の２乗と書けます。

ただ、私が見た時に、

 

 

という見方が難しいかもしれないですね。

 

しかし、それは前回の講義の月の運動を勉強しておけば理解できることであります。

円運動しながら物体をみる（非慣性系） 

 

さぁ、それでは、ここに用意された図は何かという所です。

今度はひもに結ばれているのは私です。質量ｍとします。

 

 

この時、さぁ、どうなる？？

ということは、どういうことですか？

 

 

だから、糸の張力を観測しました。

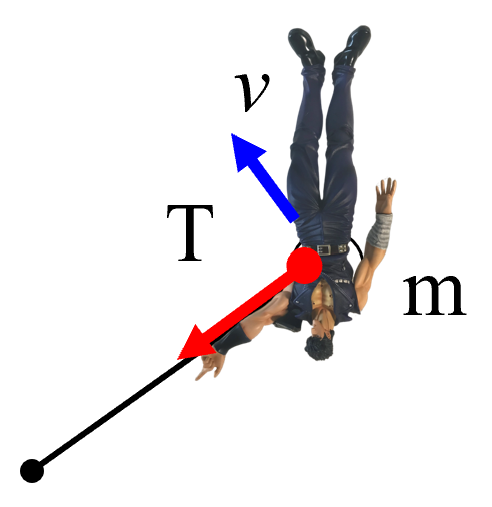
糸の張力T。

 

想像したらわかりますよねぇ…。

 

 

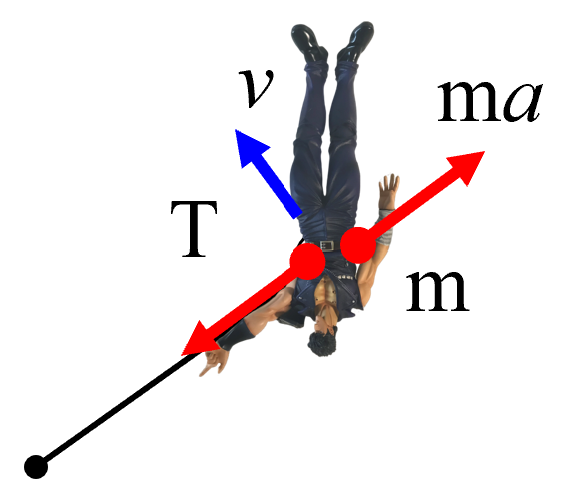
こんな力を受けるんですよ。これが慣性力です。

 

 

 

 

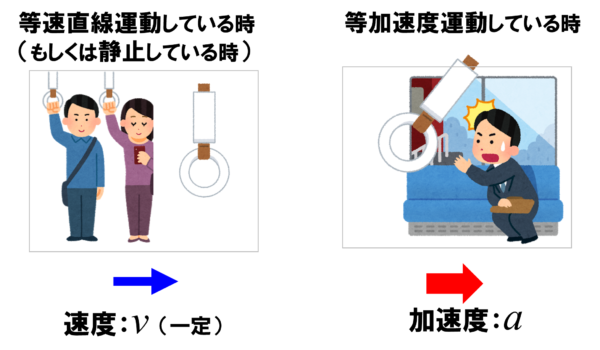
電車がガァ～っと加速度運動すると、その方向とは、逆向きにおっとっとっとってなりますねぇ。

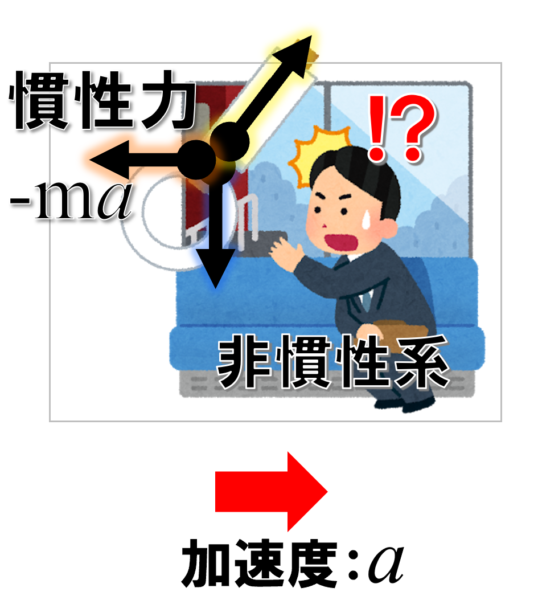
おっとっとの方向にはたらく力、加速度とは逆向きにはたらく力が慣性力。

 

 

今は私は、それに乗っかっているんですよ。

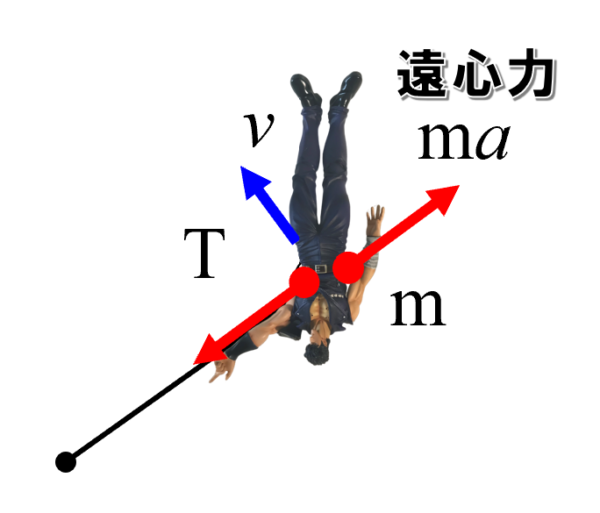
だから中心方向とは逆向きです。これが遠心力です。ｍa。

 

 

円運動は、眺める立場によって物理的意味が異なる！

遊園地の施設にひもでつながったブランコでグルグルグルグルこう回るのアトラクションがあります。

 

 

ただ座っているだけですよねぇ。

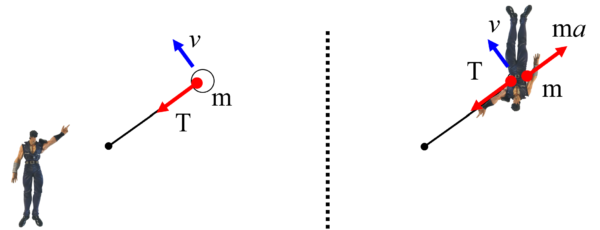
それが上図の左側の状態。そして、乗っかってるのが図の右側の状態。

だから、右側の人が慣性力を感じるんです。

 

しかし、ベンチに座っているお父さんは慣性力を感ることはありません。

以前のテーマでお伝えしましたねぇ。ベンチに座っているお父さんは、静止して眺めているから慣性系、ブランコに乗っている子どもは非慣性系。

 

下の図で言うと、左側の人が慣性系で、右側の人が非慣性系。

 

 

 

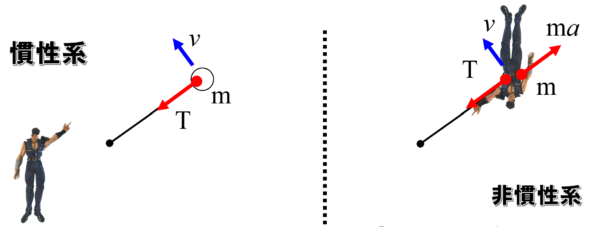
だから、力のつり合いから、糸の張力と遠心力がつり合っているようにみえます。ただし円運動です。加速度は、r 分のv ２乗です。

 

 

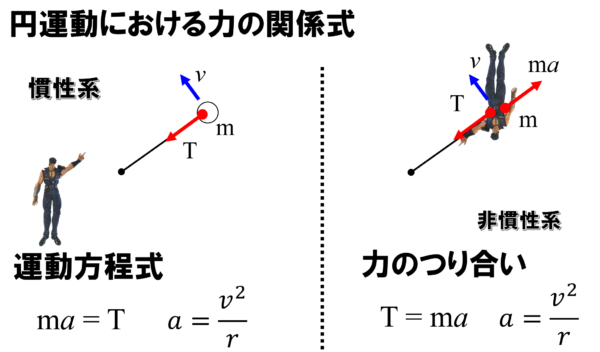
図の左側の私が見ると、

 

 

って見えるんです。だから、物体が円運動しているように見えるんです。

 

しかし、右側の私からしてみるとそうではないんです。近づく訳でもなく、遠ざかる訳でもない。

 

という見方なんです。

 

 

とても綺麗に理屈がまとまっています。だから、「あれでもない！これでもない！」という議論はちゃんと終わっているところなんです。

 

 

だから、きちんと勉強しようというわけです。

 

まとめ

 

遠心力というのは私たちの生活の中に入り込んでいる言葉である

 

それが故に円運動と言うと、みんなすぐに

 

 

って言います。

 

すぐ遠心力へ行く。すぐに乗っかるんです。

 

 

人工衛星の中に遠心力を書き込む権利のある人って、日本では少ないですよねぇ。

 

 

 

私も乗ったことありません。

 

 

人工衛星に乗ったことがある人です。

人工衛星の中でプカプカプカプカ浮いていたじゃないですか。

 

 

何故ぷかぷか浮かんでいるのですか！？

 

 

 

ロープはついていないですよ。ロープでくるくる回しているわけではないですよ。

 

 

 

でも、地上からこの人工衛星を見ると、私たちにはどう見えるか。

 

 

 

 

また、地球上に戻ってきてもらわないといけない。

 

 

って見えるわけです。

 

 

 

 

すぐに考えている物体の上に乗っかろうとします。

 

 

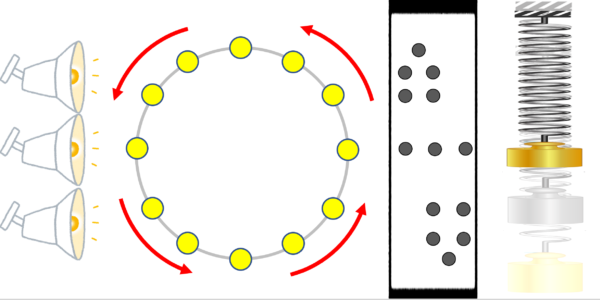
※等速円運動している物体を真横から眺めると単振動しているように見えます。

 

 

それに乗ったらどうなるかわかりますねぇ…。

 

 

 

そんなんじゃあ解けないですって…。

 

 

そうしないと思うように問題は解けません。

 

 

 

 

という発言になる。

 

 

これがすべての原因であると言っても過言ではないでしょう。

 

 

そして、最後に大事な事。片方が運動方程式で、片方が力のつり合い。

 

全然見え方が違うということ。

 

左側の人には、円の中心方向に、落ち込み、落ち込み、落ち込み続ける運動として見える！

 

しかし、

円運動する物体に乗っかっている右側の人にとっては落ち込んでません。しかし、遠ざかってもいません。すなわち、半径方向には何も運動していないものとして見える！

 

ということですね。

 

ここまで円運動について長々と説明をしてきましたが、速さ、加速度、それぞれの意味、それから力の関係式。これらを正確に理解して意味が説明できるようにしてください。