はじめに

勉強の仕方がまずいのではないかな?
と思われるところが見えてきます。

電磁気に対して、どういう風な勉強してはいけないか?
そういうところから、入っていきます。




それで根本的な解決になるか?
というと決してそうではないということです。

例えば加速度とか、速度とか、あとは何しましょう…??

垂直抗力にしましょうか…
今、加速度・速度・垂直抗力という3つの用語があります。
どんな概念を持っているものか?

1秒間にどれぐらいの距離進んだかということを速度って言うんだよ!
とか

これがもしもなかったとしたら落ちるでしょ!?
とか言いながら垂直抗力を説明するとか、皆さんは色々やると思うんです。

ところが、電気の分野になったらどうか…??

乾電池の電圧が1.5ボルトである。

コンセントは約100Vだ!
なんて言います。

じゃあボルトって何ですか?

電圧って何ですか?
それを、全く電圧というものを知らない人たちに教えようとしたときに

もともと電池って、なんなんでしょうね…??
っていうようなところです。


動くように作ったんです。
誰かが。
その誰かというのは、その根本原理がわかっている人。

根本的な原理が分かってないと作れないですよね。


この電池は1.5 v だよ!
と言ったって、それは何の役にも立ちません。

だから何なのか!?
ということが大事になってくるんです。

けれども、それは理解とは言えないので、少し難しい問題を出されたり問い方を変えられたりすると急にできなくなる。
ということになるわけです。

どこから勉強するのか?

何からちゃんと勉強していくのか?
ということを考えないといけません。

一番最初に、電圧とか電流とか電位とか、そういう概念が出てくるところはどこか?
もちろん、それは定量的なものでしたが、どこかという風に考えると…
クーロンの法則

ここをないがしろにしてはいけません。
ところが、クーロンの法則とか、そのようなところは、意外と公式をただ丸覚えしてしまえば、問題集に乗っているような問題が解けてしまうんです。

よ~し、全部できた。

もう自分はクーロンの法則が全部わかってるし、次は回路の問題だ!
というふうに行きますね。

わかることと、解ける事は別問題です。
確かに、公式はきちんと覚えていて、それに当てはめることによって

けれども、「それが本当に理解できていると言えるか?」というとクエスチョンマークがついてしまいます。
覚えるべきものと理解すべきものを、ちゃんと区別していくということが大事です。

そこでは、何を覚えるのか?

何を理解するのか?
をちゃんと分けていくことが大切になります。
主題10:電場と電位




この静電気という概念は、クーロンが出てくる前からわかっていて、その大元となる部分については、古代ギリシャ時代からわかっていました。
ただ、この時代には電気の仕業ということはわかっていませんでした。

皆さんは琥珀という宝石を知ってますか??


なんで寄ってくるんだろう…??
というような感じです。そう捉えられていたわけです。

実は、古代ギリシャでは、琥珀のことを「太陽の輝き」という意味でエレクトロンと呼んでいて、これが英語での電気(エレクトリシティ:electricity)の語源になりました。
そこが語源になっているわけだから電気の世界というのは随分と歴史が古いんですが、

なぜここから始めるのか?
っていうことなんです。

始めて式を作った人
つまり定量的に電気を捉えようとした人だからです。

、避雷針-600x374.jpg)


例えば、その雷がどれくらいの電気を持ったものなのか?
ということについては述べていないわけです。

ですから定量的なところからスタートするということで、クーロンの法則から入っていきたいと思います。
①クーロンの法則

クーロン力といいます。点電荷に働く力。
これに関する式を作り上げたクーロンという人の名前に力がついてクーロン力。

点電荷とは、電荷を持っているんだけど点である。体積とかそういうものがないという訳です。
例えば仮に、図のように+Qクーロン、+qクーロンの電荷があったとします。


それに対して例えば+Qクーロンに-qクーロン。
こういうものがあるときはプラスとマイナスですから、引き合うわけですね。


これがどれくらいの力で引か合うか?
ということを求めたわけです。

距離の2乗に反比例し、
要するに離れれば離れるほど力は弱くなり、

こういう式を実験によって作り上げました。
実験で得られたということですから、覚えてもらわなくてはいけません。

ここで非常に重要なことがあります。
それは何かと言うと

実はこの F。これは力の大きさしか表していません。
向きは表していません。右向きとか左向きということは式には現れません。

あくまでも大きさです。
ですから、ここで注意しておきたいのは、

ということですね。
そして、もちろん力も大きさであるということです。

それじゃあ、向きは一体どうやって判断するんだ!?

先ほど判断しました。
プラスとプラス、マイナスとマイナス、と同符号だったら反発力。

この力を斥力と言いますね。
逆に異符号。プラスとマイナス。
この場合は、引力という風になります。

斥力のことを反発力と呼ぶ人もいますけど、高校生程度であれば斥力という言葉のほうがいいかも知れません。よく使われる言葉で入試問題なんかにも出てきますから、それはしっかり押さえておいたほうがいいでしょう。
これが、まず点電荷に働く力の式になります。

もしかしたら…、
すでに気付かれている方もいるかもしれないんですが

何かに似てませんか? これ。
例えば電荷Qとqが質量M、mに置き換わったら、それは万有引力、
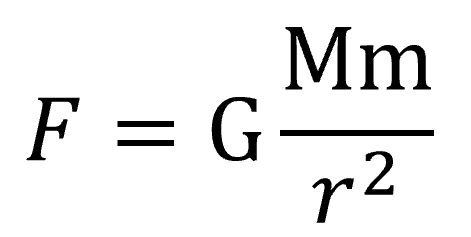

そっくりですねぇ。
実は、多くの科学者たちはこのクーロンの法則が発表された時に

すごい!!
と。

万有引力と同じ形をとっている。
万有引力というのは、ニュートンが1600年代後半くらいに見つけ出したもの。それに対してこの式が出てきたのは1800年代なんですが、式の形がそっくりなんです。

こういうところから物理学では、この類似性…アナロジーが非常に重要視されていくんです。
地球の周りを月が回っているのは、万有引力のせいですね。

それじゃあプラスの周りを電子が回っているんじゃないかな…??
実はこのクーロンという人、一説によると、ちょっとした逸話ですから本当かどうかはわかりませんが、
きっと万有引力みたいな形になるんじゃないか?
と予想してたという風に言われています。

しかし、その論文の中には予想してたということは書かれていないんですねぇ…
だから、本当かどうかよくわからないんです。本当かどうかはわからないけど、クーロンがそれによって賞賛されたことは事実です。

素晴らしい力を見つけた!!
だから、これは実験によって出てきた式ですから覚えてください。
②クーロンの法則による位置エネルギー

実験やって、こんな力になりました。万有引力の形とそっくりですよ!
っていう訳です。それはいいんです。

問題なのはここからです。
こういう力が見つかったということは、

もう一つ物理量が定義できる。

それが何かというと…
位置エネルギーです。

今、新しい力が見つかったから、この力に逆らってどうのこうのっていう議論をしてあげればクーロン力による位置エネルギーというものが定義できるようになります。
だからここで定義をしていきたいんですが、これは万有引力の時と同様なんです。

積分を使わなければいけなくなる。
ですから計算式なんだけど、その式は覚え方がいいと思います。クーロン力による位置エネルギーは、静電エネルギーと呼んだりすることもあります

静電エネルギーというのは、コンデンサーのエネルギーじゃないの?
って、言わないで下さい。

あれも位置エネルギーですから。
クーロン力による位置エネルギーのことですから、もう式をいきなり書いてもいいでしょう。微積分から出てくるんですね。一般的にUという記号で表すことが多いです。

実際には計算式です。

しかし、高等学校であまり微積分に立ち入るのをやめましょう!
ということですから、覚えていいところですね。
位置エネルギーの基準点は??

ところがです。
そのままにはできないことがあります。

それは何…?
例えば、万有引力の法則がありました。
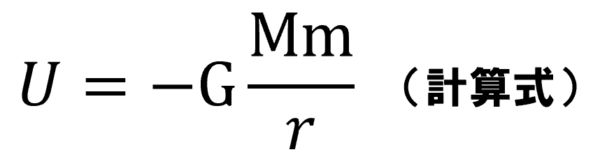

万有引力をrで積分すればいいんですね。
すると、この式になります。

今回…同じなんでしょ? 形が。

それなら、位置エネルギーだって同じでいいじゃないですか?
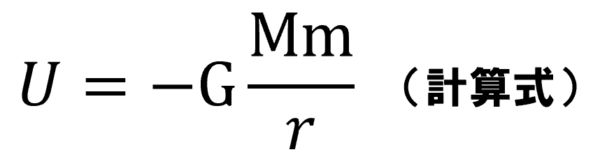


なんでクーロンの法則による位置エネルギーの式には、マイナスがついていないのか?
数学的にマイナスをつけたっていうのはわからなくもないですが…

困りましたねぇ…。
そうなんです。元はベクトル量なんです。力っていうのは。ですから向きがあるわけなんです。それに対してこういう式を丸覚えしても、何も意味を持たないですね。

位置エネルギーの式にマイナスがつかないことについて、少し丁寧に考えてみましょう。

基準です。

どこから考えるか?
ということです。

例えば4階にある自宅の床を基準にするのか??
それとも、ここは7階建てだから、1階を基準にするのかで位置エネルギーが全然違ってきます。

基準となるのは、位置エネルギーUが0になる位置。

Uが0になる場所ってどんな場所だろう…??

それは、位置エネルギーの式が0になるんだからrが無限大にならざるを得ません。
ですから基準は無限遠。これが基準になるんです。

だから、遥か彼方が無限大。

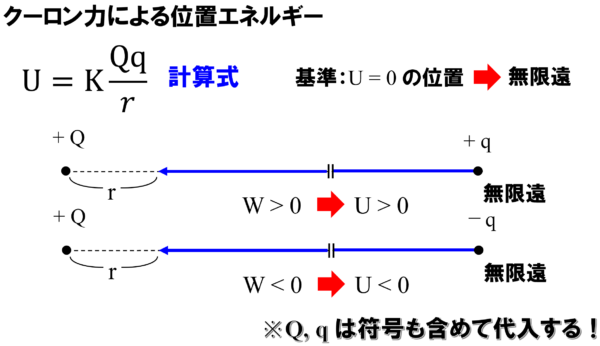
位置エネルギーの符号について

さぁそれでは、位置エネルギーってのは一体何だったかということをもう一度考えてみます。
力学の時には、万有引力に逆らって、どこまで持っていくかっていうようなことを考えました。mgに逆らって物体をどこまで持っていくかと考えた。

それでは今回はクーロン力に逆らって、どんな仕事をしたのか?
ということを考えたらいいわけです。


この+qクーロン。これは無限遠にあるんです。
これをよっこいしょ、よっこいしょ、よっこいしょって


ここから距離rのところまで持ってくるのに必要な仕事がいったいどのくらいか?
ということを考えます。

出来ることなら近づきたくない。
そうですねぇ。反発力、斥力が働いている。

そうすると私はしんどい思いをしないといけない。
ということは私がした仕事Wは、

正の仕事をしたことになる。
正の仕事をしたということは、もちろんその結果として位置エネルギーを持つわけですから位置エネルギーは正である。

こうなります。

これは斥力が働いた時です。

それでは、引力が働いたときは…??
もう簡単ですねぇ。それでは、次に左側を+Q、そして今度は右側をーqにしてみます。

ところが…

さぁ、これをぐぁ~~って、持っていくって言っても…
さっきやったのは反発力。斥力が働いてるから持っていくのが大変だったかもしれませんが、今度は+Qとーqです。

勝手にスゥ~っていきますよ。
だから私が持って「ぎゅぅ~~っ」て、やるんじゃないですねぇ…。

「おぉ~っ」て、引きずられてしまうんですねぇ。
ですからその場合は負の仕事ということになります。


さぁ、困りましたねぇ…。
万有引力のときは、質量は絶対に正ですかね。問題ないんです。

困りました…
そこで、覚えておく式はこれだけにしておきましょう。

万有引力みたいにマイナスをつけるのはやめましょう。
その代わりに、式にQqって書いてあるけど、それは便宜上書いたんであってこう言う風にしましょう。

+Qと+qを入れる。
そうするとUは正になる。

+Qとーqを入れる。掛け算するからマイナスになります。そうするとUは負になります。
これなら、ちゃんと物理と一致します。
しかし、クーロン力による位置エネルギーはQqは符号も含めて代入してあげればいい。+かーも含めるんです。

どこからどういう風にして位置エネルギーという概念が生まれてきているか…??
というようなことを少し重要視して頭の中に入れておいてください。

実は、クーロン力というのは実験式ですから覚えればいいんです。
位置エネルギーの式も覚えてしまうんです。

覚えて良いんです。
いちいち積分とか使うのは大変ですから。

「ぐぅ~~っ」と持っていくのがしんどい…。
とか、

あぁ~~、引きずられる…ってやりましたねぇ。
実は、その概念がちゃんと頭の中に入ってるかどうかって言うところに、問題を解くときの力の差が出てきてしまうんです。
■単振動の問題解説(制作中)
















