はじめに
今回は気柱の共鳴にまつわる問題を見ていきます。
よくある問題なので、丁寧に解説をしていきたいと思います。
問題解説
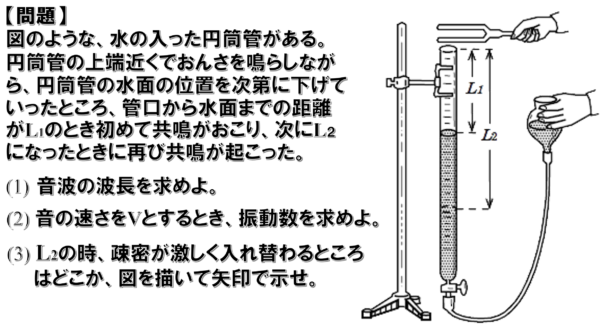
一端が水で区切られた気柱です。
おんさを開口付近で鳴らして共鳴実験を行います。

片方の口は開いていて、片方は水で塞がれているからこの気柱は、閉管に分類されます。
定在波ができると、大きな音が出ます。
おんさを使って音を出しながら、ゆっくりと水面を下げていきます。

気柱の長さを少しずつ変えていくんです…
すると開口からL1のところで、初めて音が大きくなる…

あぁあぁ、
なるほどなるほど。

ちょうどL1だけ行ったところで、固有の定在波ができたんでしょうねぇ…。
さらにL2のところで再び音が大きくなった。
ゆっくりと水面を下げて行くと、L1のところでまず大きくなります。
それから、またずらしてしまうと、定在波が出来なくなるから音が小さくなります。

それから、ず~っと下に持っていくと、次のL2というところで再び音が大きくなったというわけです。
(1)解説
それでは、1番から考えて行きます。
音波の波長を求めなさい。

何か難しいですねぇ・・・。
どうやってやればいいのでしょう??

「私たちに与えられた条件は、L1のところL2のところで定在波ができたよ!」という条件。
これしかありません。

それに対して一体私たちは何をやればいいのか…?

いやいや、
迷う必要はありません。
定在波の絵を描けばいいんです。
ここに気柱があるとします…

そして、それに対して開口から音を送り込んでるわけです。
それから・・・ゆっくりゆっくりと、水面を移動させていく。
するとあるところで、定在波が出来るんです。


そして、また消えて、「ず~っと行くと、また定在波が出来た。」と言っているんです。
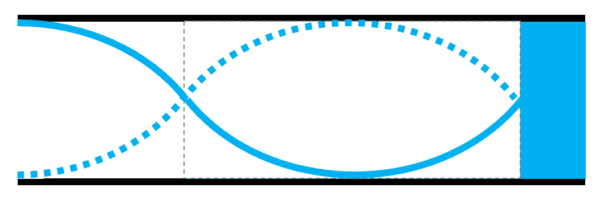
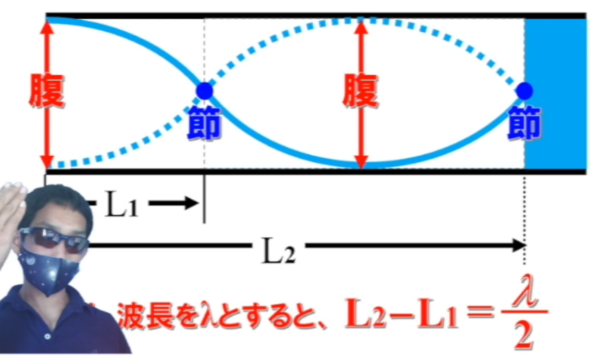
その時に、何をやればいいかというと、開口は絶対に自由です。
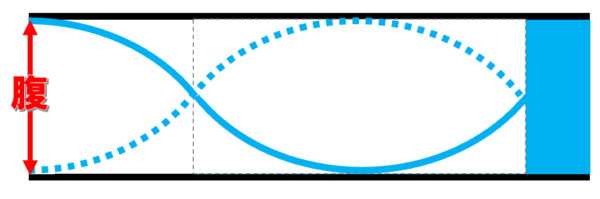
ここでは空気は、自由に動き回れるんです。(だから定在波の腹になります。)
ところが、音は縦波ですから…、壁のようなもので仕切られてしまうと、空気は動けないです。

水で仕切られた所は節なんです。
そうするとある場所で、まず、こうなったんです。
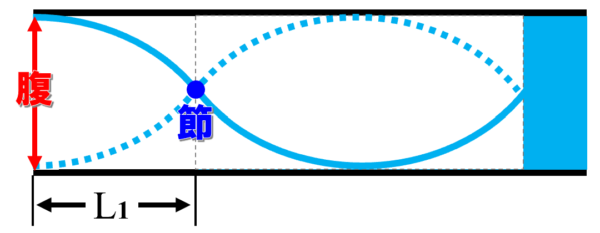
これがL1です。

次に行きます。
さらに水面を下げて行ったら、また共鳴が生じた。

これは閉管ですから偶数倍振動にはなりません。
奇数倍振動です。
そして、基本振動の波形が1個です。
その次ということは、基本振動の波形3個分です。
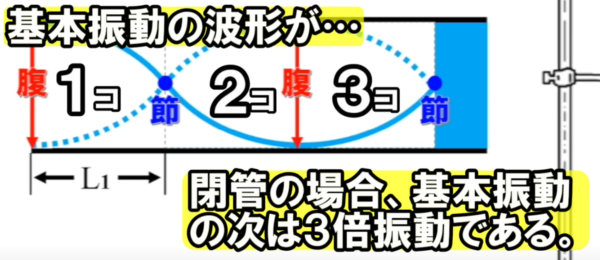
この形が1,2,3個。
ここが、L2、という場所だということがわかります。
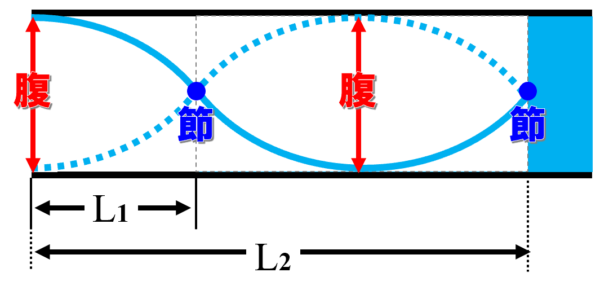

こうやって赤い印や青い印、つまり腹や節を書き込むことによって、定在波の形を書いてあげる。そうすると私たちは、情報を得ることができるんです。
節から節までの距離は、λ/2 です。
そうすると、図から容易に求めることができます。
図より、L2 からL1 を引くとλ/2 に等しい。
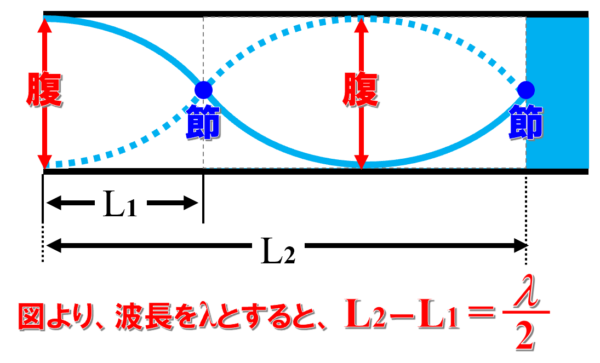
よって、λというのは、2倍のL2 引く L1
![]()
これで出来ました。
(1)補足:開口端補正値について

ただ、ここで少しこだわっておかなければいけないことがあります。
それはどういうことかと言うと…、

皆さんの中には、これに疑問を感じた人もいると思うんです。

先生なんでそんな面倒くさい事するんだろうなって…、

僕はもっと簡単に解けました。

そうなんです。実は。
ここを見て下さい。ここはL1 です。
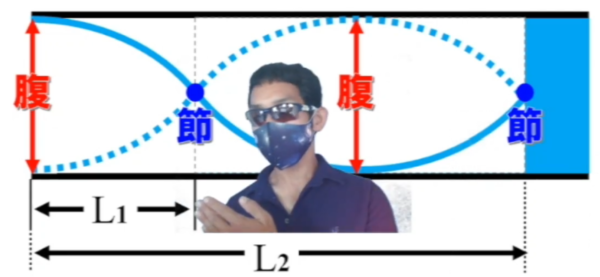
これがL1 だっていうことは、この区間は λ/4 じゃないですか ??

じゃあ、λ/4 はL1 に等しいんじゃないですか?
![]()

おぉ、ほんとだぁ…。
なってる。

なんなんでしょう。この答えは…?
図より、L11個でλ/4 が1個入った分じゃないですか。

それならλって、4L1 っていう答えじゃいけないんですか??
題位としてはL1 とL2 が与えられています。

ですから、解答で示した答えが、私は良いと思います。

しかし…、これだって物理的におかしくないです。

ただ、この答えというのは、開口端補正値が無視できる場合の答えなんです。
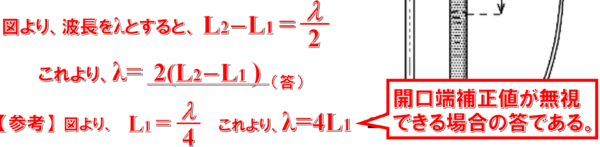
それでは、

この、開口端補正値とは、一体何なのか…?
という話をしないといけないのですが、

開口端補正値というのは、概念としてはこういう概念です。
1番の問題を解くために定在波の図を書きましたが、開口の赤い印の場所は、実際に実験をやってみるとピタッと、ここに一致しないってことが分かっているんです。

すなわち、腹の位置がちょっと外へ出るんです。
そういうことがわかっているんです。

その外へ出たもの、そのほんの少しずれた分。
これを開口端補正値と呼んでます。
ですから、本来ならば、ここに気柱があるとすると、その時に、極端に言うと、こんな場所が定在波の腹の位置になるんです。
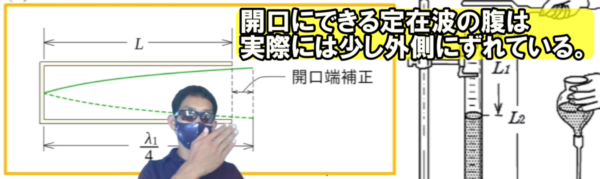
そうすると、こんな波形になって、開口から少し外にずれた位置から左端がL1 なんです。

そうすると、λが4L1 というのが嘘だって、わかります。
ここの部分のずれがあるから、L1 がλ/4 にはならないです。
開口端補正値っていうのは、高等学校で学習する数学だけで理論的に求められるものではないんです。

ですから解説としては省いても構いませんし、入れてもいいと思うんですが、開口端補正値を考慮しなければいけない時には、この解答は合いません。
しかし、そういうことを考えなくとも、間違いなくこちらの解答は絶対に成り立ちます。
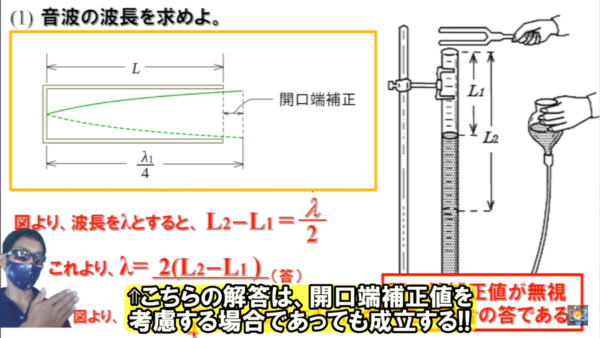
ですから、開口端補正値が無視できるとして、ここまで解いてきましたが、L1 もL2 も両方与えられている場合の問題では、こちらを解答にさせてもらいました。

実際に問題を解くときには、問題文に開口端補正値は無視するなどの但し書きがあるので、注意してみるようにしてください。
これで1番の解説は終わったので、次に行きます。
(2)解説

音速をVとする。
音の速度をVとすると、
音の振動数はいくらですか?

これは簡単です。
もう波長を求めたから、波長は分かっています。
そして、音の速さがVである。
この時、振動数を求めなさい。

これは、波の基本式v=fλ
λ はさっき求めました。
2倍のL2 引くL1 です。
fというのは、V/λ です。

したがって、答えは、2倍のL2引くL1分のV となります。

物理が得意な人からすると、

なんで、こんな簡単な問題が出たんですか??
って言われるかもしれませんが、

よく教科書などに、振動数…
例えば、今回やっている片方が閉じている場合の気柱は、m倍振動の時の振動数はこう書きますとか言って、式が書いてあります。
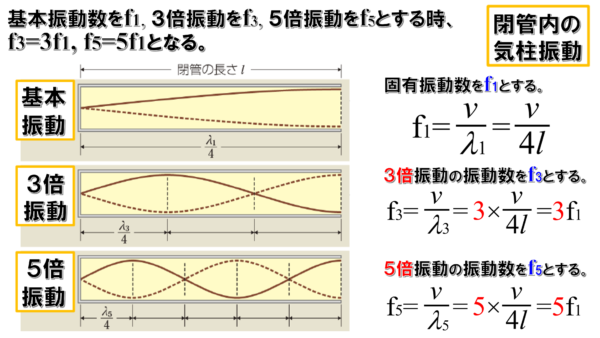
それを見た人の中には、教科書を書いた人の意向とは関係なく、

あぁ重要なんだぁ!
と思ってしまって、公式として覚えてしまう人がいるんです。

確かに成り立つ式ですから「覚えてはいけない!」とは言いません。
しかし、これがどこから出てきた式なのかって聞くと、答えられない人がいるんです。

それでは困るんです。
そして、人によっては、この問題を教科書の公式を使って解こうとするから、

3倍振動の時の振動数は、何だっけ…

思い出せない‥‥
となって途端に全く手がつけられなくなってしまうんです。

要は、これはただの基本式なんです。
v=fλです。
高等学校で学習する波は、この式を基礎にして、縦波とか定在波であったり、音の性質を見ているんです。
だから、基本振動だろうと3倍振動であろうと、使える式なんです。

そうして見ていくと、教科書に書かれている、こういった式を覚えるというのは、V=fλを覚えて、さらにf=λ分のvを覚えたっていうのと、何も変わらないんです。
だから、そこまでしなくていいんじゃないですか。

どうせ絵を描いてしまえば、波長はわかるんわけですから、
絵を書いて波長がわかれば、v=fλに代入するだけじゃないかと…。

それでいいんじゃないでしょうか…。
確かに公式も大切です。

しかし、導く過程はもっと大切なんです。

どうやって出てきたかが説明できないで闇雲に覚えて、それに数値を代入して出来たからと言っても、物理がわかってるかって言うと、そうではないことはわかって頂けると思います。
そういうところは、勉強の時に気をつけてください。
(3)解説
それでは、次の問題に行きます。

3番… これは難しいです。
L2 の時、疎密が激しく入れ替わるところはどこか、図を描いて矢印で示せ。

何をやったらいいかわかんない人が、たくさんいるんじゃないでしょうか。
それでは、早速やってみます。
「図を描いて矢印で示せ!」と書いてあります。
なので、まずは、こんな絵を書いています。
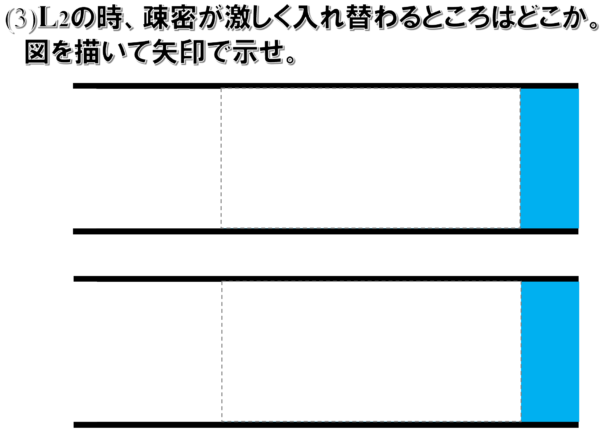
これは皆さんもマネしてみてください。
L2 の時ですから、ある時はこうです。
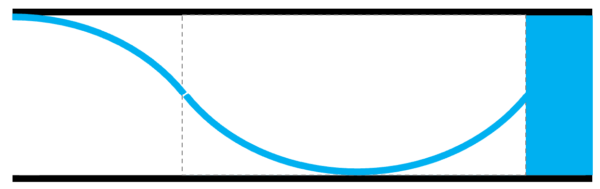
そして、ある時は、こうです。
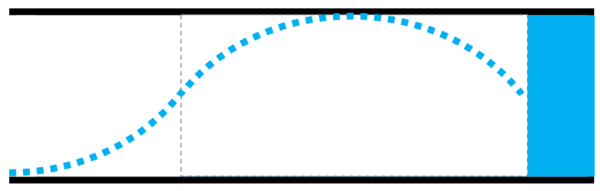
この後の説明をわかりやすくするために、真ん中に薄~い線を一本引いておきます。
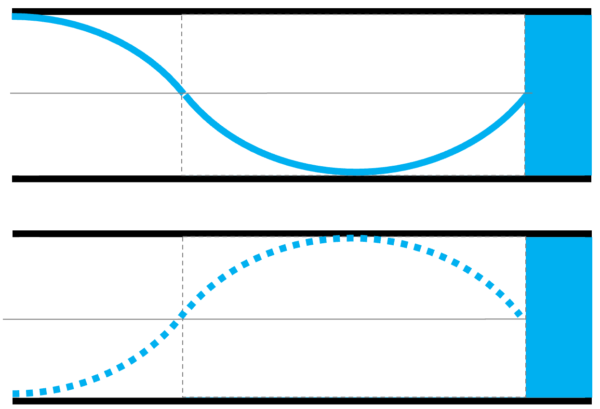
これから、疎密を調べていきます。
これは、音です。音っていうのは縦波ですから、疎と密が入れ替わる疎密波です。

ところが、あたかも横波みたいに書いてあるんです。
でも実際は違います。

これは縦波を横波表示しただけなんです。
【参考】
だから実際には、上下に動いてないんです。

音だから、左右に動いてるんです。
それを90度パタッと反時計回りに回転させて、こういうふうにしたんです。
そうすると、

こっからここ(節から節)までが、2分の1波長だね!
とか、わかりやすいから、こういう風に書き換えたんです。

しかし…、疎密を見るためには、戻してあげないといけません。
だから、これから戻していきます。

まずはここです。
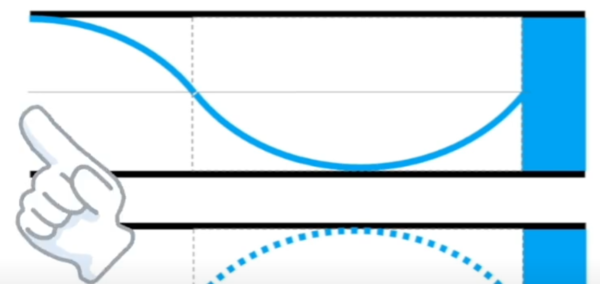

上に行ってるということはどういうことですか?

正に行ってる。

本当は右側に移動してるんです。
ここは、こうなってるんです。
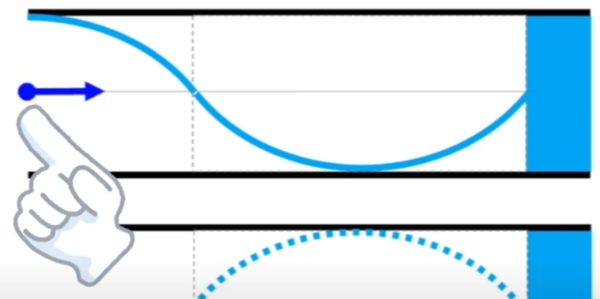
ここは…負です。
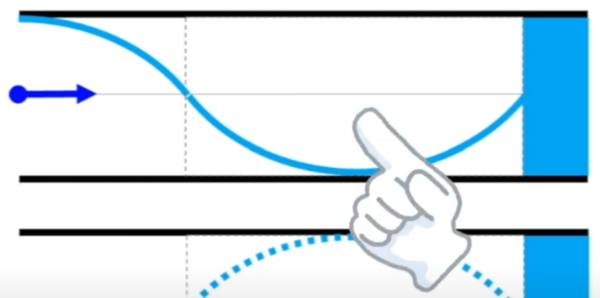
下に行ってるけど、本当は左に行ってたんです。
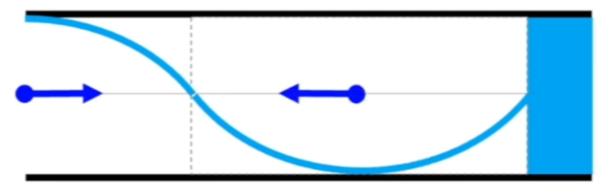
同じように、負です。
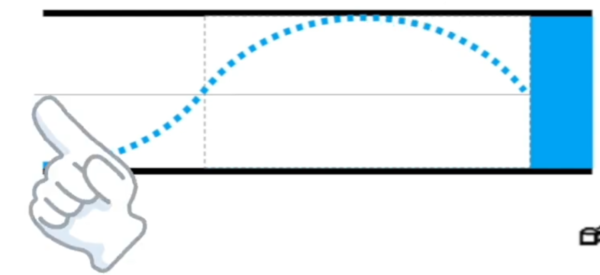
そうすると、左です。

正です。


右だ!
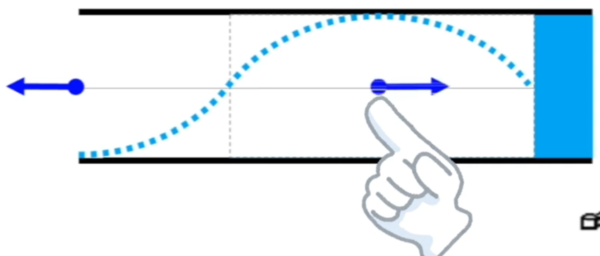

わかってもらえましたか…??
ここが、密…。ここが、疎…。
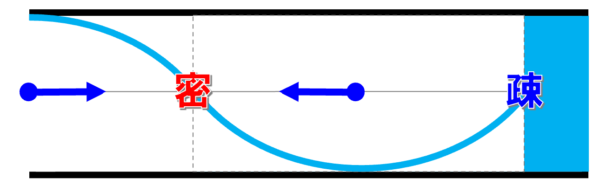
ここは、みんなが逃げちゃった。だから疎。
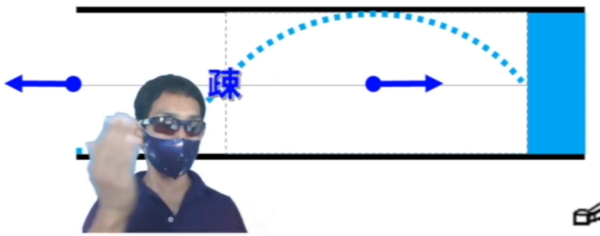
ここは、グッと集まって来た。だから密です…。
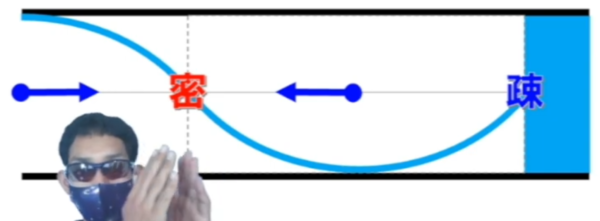
ここには実際にピストンがあるんです。だから、ここは空気は動けないんです。
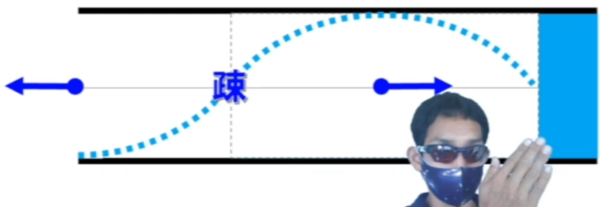
それに対してビュ~って来るんです。
だから、密集します。

それで粗密が激しく入れ替わるところはどこですか?
矢印で示しなさい。

それは、こことここです。

だから、どこなんですか??

それは、節です。

節の場所が疎密が激しく入れ替わる場所である…。
ということが分かります。

これは覚えるところではありません。

疎密が激しく入れ替わるところは、確か…節だったなぁ…。
とか、そうではなくて、矢印書けばこうやって、疎になったり密になったりすることはすぐにわかります。
前回の講義でバネがビヨ~ンて伸びたり、ギュ~んと縮んだりとやりました。あの疎密のことを思い出したらいいんです。

みんなが逃げてんのかなぁ…。
集まってるのかなぁ…。

それだけでわかるはずです。
参考:空気の圧力変化と疎密の関係
最後に、参考ということで、3番の問題では、疎密が激しく入れ替わるところを確認しましたが、

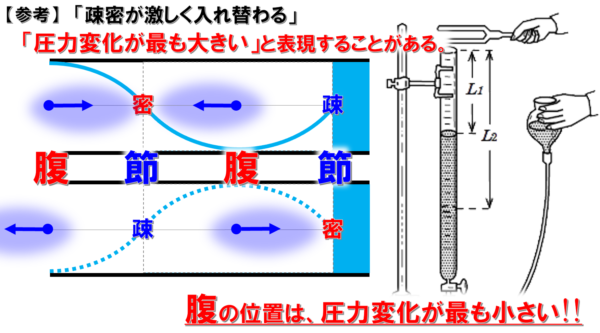
この「疎密が激しく入れ替わる」ということを、「圧力変化が最も大きくなる」という言葉で表現することがあります。
このことについて、クントの実験で有名なこちらの装置で、3倍振動する気柱内部の様子を確認してみます。

節の位置と腹の位置は、ここの部分になります。
一見したところ、節の位置には、何もなくて、逆に腹の位置が盛り上がっているから、

腹の方が疎密が激しく入れ替わったり、圧力変化が最も大きくなるんじゃないか??
と思いたくなるんですが、ここではこのように解釈してください。

「疎密が激しく入れ替わる」の主語は「音」を伝える媒質、つまり「空気」です。
ですから、「空気の疎密が激しく入れ替わる」とは、どういうことかを考えないといけません。
そこで、節の位置を見ていきますが、

空気の疎密が入れ替わっている…
空気の疎密が激しく入れ替わるということは、ここに空気が集まったり、ちらばったりするわけです。

節の位置を起点にして、空気が左右に行ったりきたりするから、そこには、それ以外の粒子が入り込む余地がありません。

ちょうど、この位置では、ほうきでホコリを履くように空気が粒子を外側に押しやっているわけです。
逆に、腹の位置。
ここでは、空気は大きく振動しているわけですが、このあたりの空気のまとまりとしてみると、
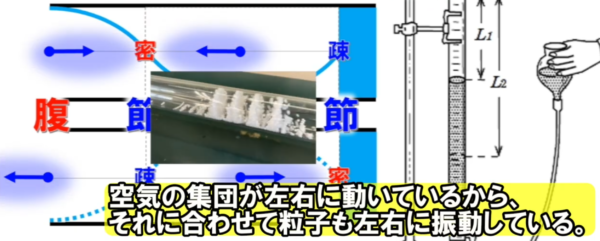

このまとまりが、左にずれたり右にずれたりしているだけなので、空気の密度は、それほど変わらないというわけです。
だから、節の位置は圧力変化が最も大きくて、腹の位置は圧力変化が最も小さくなる訳です。
今回は、具体的な波ということで、音の性質を見て行って、その中で弦、それから気柱、そういうものを扱ってきました。
一見したところ難しく感じるかもわかりませんが、今までの基本的なところがわかっていれば、十分応用が効くと思います。
大切なのは、今出来上がっている波を正確に図示できるかどうか、図で書くことができるかどうか。
それさえ、出来てしまえば、あとはそれを数式にのっけるだけです。
それは、決して難しいことではありません。
物理にとって、波動にとって、最も大切なのは今出来上がっている波を如何に正確に書くかです。
是非、それに気をつけて問題を解いてみて下さい。















