
はじめに
それでは、講義編に引き続き波の例題解説の方に移っていきます。
□講義編(前回の復習)
波の例題解説
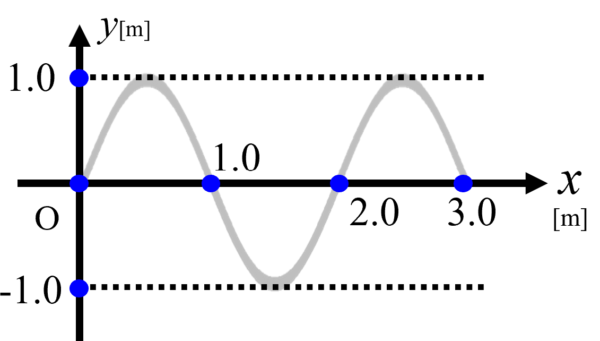
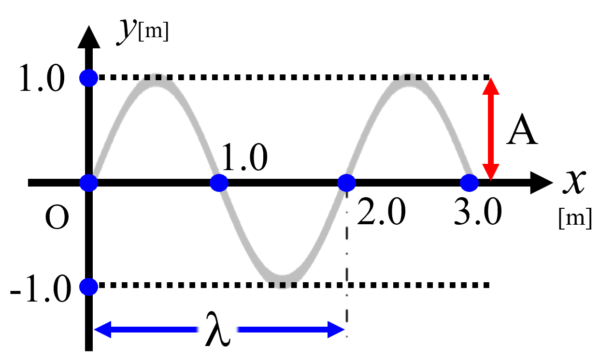
図はX正方向に進む波を表しています。長さの単位はメートルです。

x軸と曲線が交わるところで、1.0, 2.0, 3.0 とそれぞれ目盛りが打ってあります。一方、y軸は上に1.0、下に-1.0となっています。
この図に関する問題を今から考えていきます。

1番は簡単な問題ですので、さらっと進めていきます。
(1)解説
振幅A、波長λはそれぞれいくらか。

振幅というのは、どこの量だったかと言うと…
元々ロープがあった場所、それがちょうどx軸になっています。
そのx軸から最大変位までということですから、振幅Aは図に示す位置にあることがわかります。
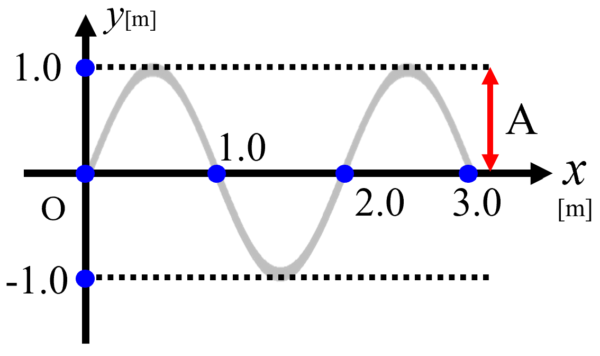

続けて波長も見ていきましょう。
図を見ると、ちょうど原点から2.0の位置に1波長分波が描かれています。したがって、波長は図に示す区間であることがすぐにわかります。

したがって、振幅と波長は、グラフから直接読めます。
グラフより、Aは、1.0メートル波長が2.0メートルになります。
次の問題にいきます。
(2)解説
例題の図は、ある瞬間がこうだったというグラフです。
いつもグラフがこの形になってるわけではありません。

ですから、この波のグラフというのは、「しばらくするとx軸正の方向に進む波である。」と書いてあります。
だから、右向きに進んでいくわけです。


そして、「0.5秒後に見てみたら、こういう風に進んでいましたよ。」ということです。
その進んだ距離というのが、2.0メートルと書いてあります。

ということは、等速で伝わるわけですから、等速の式を使えばいいですねぇ…。
等速で伝わることから、進んだ距離は、速さ×時間のはずです。
進んだ距離は2.0メートルそれがイコール、速さ×時間。

時間は0.5秒間です。
ということで、解答は次のようになります。

従って、1秒間に4メートルだけ進む速さということになります。

こういう所の計算は波動っぽくないというか、小学校とか中学生でも出来そうな計算です。

出来そうなんだけど…

小学生や中学生には、「波形が本当は右側へずっと動いてるんですよ!」っていう考え方は、なかなか難しいですね。
だから、波動の問題に対して解答を見て、出来上がった式と答えを見てしまうと、

なんだよこれっ!
(簡単だったじゃないか…)
って、いうようなものかもしれませんが、かなり難しいことをやっているんです。
それでは次の問題に行きます。
(3)解説
波の周期Tはいくらか。

困りました…
波の周期。周期というのは、例えば手で動かして波を起こしているのであれば、
1回上下に振動させるのにどのぐらいの時間を要しているか!?
と言ってるんです。

一度、考えてみます。
原点の位置を波源と見ればいいです。
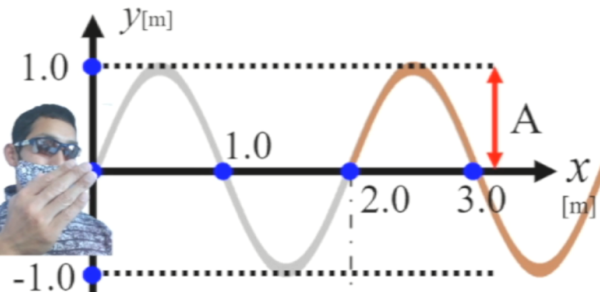
ここを波源と見て行って帰ってくるまで。

要は、行って帰ってくるまでの時間が欲しいんです。
それがどうすればわかるかっていうことなんです。
ところが、行って帰ってくる間には、波がちょうど1波長、進んでいるはずです。

あーなるほど!
だから2番で速さを
求めさせたんだ。

(2)の問題では、グラフに書かれた情報を一切使っていないですねぇ。
問題文の2.0メートルと0.5秒を使って割り算しただけです。
2番の問題は3番の問題を解くためのヒントになっていたわけです。

速さ v は「1秒間で4メートル進みます!」という意味です。
1秒間で4メートル進むんです。
そして、
1つの波は2メートルです。

これでわかってもらえましたか??
![]()
これから行きましょう。

v は4.0m/s λは2.0m。

vの単位は、メートル毎秒だから大丈夫ですね。単位が揃っていない場合がたまにあるのでここは注意してください。
波長がセンチメートルで、速さがメートル毎秒だったら、波長をメートル単位に揃えないといけません。
これより、答えは0.5秒となります。
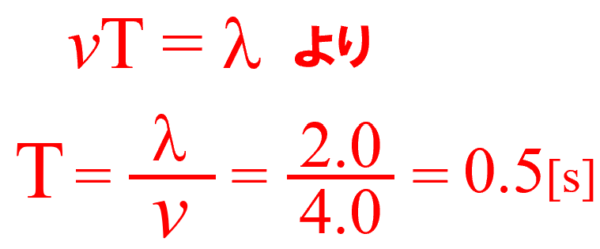
物理って言うのは、少し勉強してみると分かると思いますが、vT=λの式に気づかなかったりするんです。

これは物理を一通り学んだ浪人生でも多いんです。この式に気づかないんです。模擬試験とかやってても。
それで解答を配られてから、答えを見るんです。

それで、なんだぁ…
簡単じゃないかないか…!?
って言うんです。
でも解けなかったんです。

なぜだかわかりますか?
vT=λという式は、知ってるんです。

でも覚えただけだから、どこで使っていいか分からないんです。
今回の場合であれば、いったん問題を読んだ瞬間に、困らなきゃいけないんです。
波のグラフが与えられていて、て行って帰るまでの時間(周期)を求めよって言われても、

そんなの無理だろう!
って、

何かいい方法はないだろうか…
と。

それから、何度も波源のところへ行って帰ってくる様子を想像して見るんです。
すると、

そうか1周期の間に進んだのは1波長分だ。
そうなった瞬間、この式だって、すぐにわかります。

ということは、vT=λという式が、ちゃんと和訳できないと、ダメなんです。
そして、出てきた結果は0.5秒です。
0.5秒間に1つの波を出すんです。
1秒間あたり4メートル進んだんです。
そして、波長λは2.0メートルなんです。
どうってことはないんです。

そして、今度は逆に言うなら、λとvをを見れば、すぐにわかるんですよね。
λは、1秒間に進む距離の半分です。
1秒間の半分っていうことは、0.5秒の間に1波長分進んでいるということです。

じゃあ、それは1周期に等しいですね。
和訳ができている人にとって、とても簡単な話なんです。
それでは最後の問題です。
(4)解説
波の振動数f はいくらか。
簡単ですね。こうです。
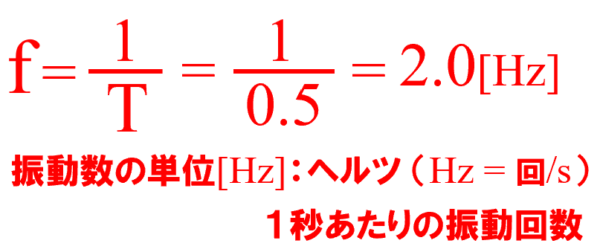
講義のところでやったから大丈夫ですねぇ。
それで、もう少し話は続きます。

「終わった終わったぁっ!!」て、先に勉強を終了しないでください。
f=1/T=1/0.5=2.0Hz となりました。

だから、何なんですか?

1秒間に2回振動しているということです。
それはそうでしょう。

1秒間に2回振動しているということは、1秒間に2個の波を出してるということです。
1秒間に2個の波を出している。1個あたり2mです。
1個あたり2mということは、2個出せば4m。

4m進んでます。
それでは、ここで別の解き方を紹介しておきます。
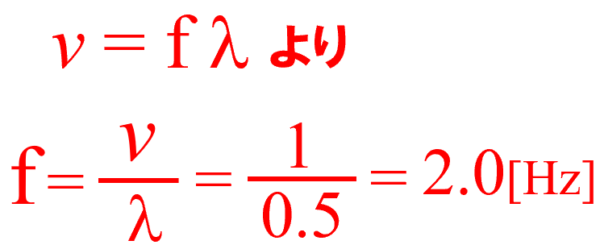

さぁ、なぜ私がこれを取り出してきたのか?

あぁ、あの公式ね!
って言うのは無しです。

そうじゃないんです。
振動数を求めなさい!
って言われた瞬間に振動数っていうのは、
1秒間あたり何回振動しているか?
言ってみれば、1秒間あたり何個の波が出てるかということです。

そうなった時に、「どういう式を使うべきか!?」ってのが浮かんでくるんです。
4番の解答として、簡単なのはもちろんTが求まっているから

T分の1ってやりゃ
いいんじゃないか!?

それは答えを求めるためだけにやっただけなんです。
今は波動というものの理解を深めていきたいんです。
だから、こういうことを一生懸命やっているところなんです。

私は、前回の動画の一番最初に言いました。「波動が苦手な受験生が非常に多い…。」と…。
それは、このあたりの問題を記憶で解いているからです。
わからなくなったら解答を見て

あぁそうか、あの式を使ったのかぁ…

それを避けなきゃいけません。
そうすると、図のλ/v、v/λのところをよーく見てください。

もちろん逆数になってます。
その逆数になることを上手く利用したのがここなんです。

そうすると、λが2.0、vが4.0で、fは2.0ヘルツとなるわけですが…

なぜ、こんなことをやったのかわかってもらえますか…??
4番のこの解答を見てください。
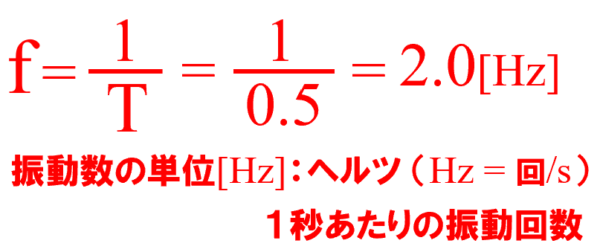
この解答は、Tが求まらない限りこの結果を出すことはできません。

ところが別解であれば、Tを求める必要なんかないわけです。
2Hzって、答えてくるわけです。
さっき求めた3番の答えがあって、それを利用して f=1/Tの式を作っていますが、

じゃあ、問題を作る人が3番の問題を作らずに、4番が3番だったらどうしますか?
「いきなり振動数を求めなさい」っていう問題があって、(3)の問題がないわけです。
そうなった時に、さっきの解法は使えないわけです。
その時に、別解の方へ逃げていくんです。
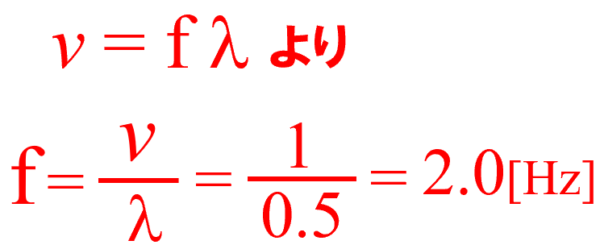

じゃあ、何が必要なんですか…?
振動数って何か?
っていうのが必要なんです。
振動数とは、
1秒間あたりに出した波の数に等しいんだよ。

波1個あたりは、λっていう距離だろ!?

それじゃあ、fλっていうのは1秒間進んだはずじゃねえか !?
こういう風に考えるから、

こっちはv=fλ使えば簡単だ。

周期なんていらない!
という話になってきます。

だから、この3番と4番の解答を見てしまえば、どうってことない問題に見えるんですが、こういうところが波というものを正しく理解させてくれるわけです。
まとめ
それで、問題は全部解けましたので、もう一度最初のグラフの形に戻りたいと思います。

まず皆さんはこういう問題を見た時に、どんどんどんどん公式を思い出すとかいうような作業をするんではなくて…
まずこの絵はパッと見て

1波長ってここだったな。

ロープが元々あった所からの最大変位までが振幅だったな。
ということをまず確認します。
そこまではいいでしょう。

それで、その後に2つのことを必ずやってください。
その2つの事というのが、まずは原点の位置でロープを持って上下に動かしているんだなぁ…
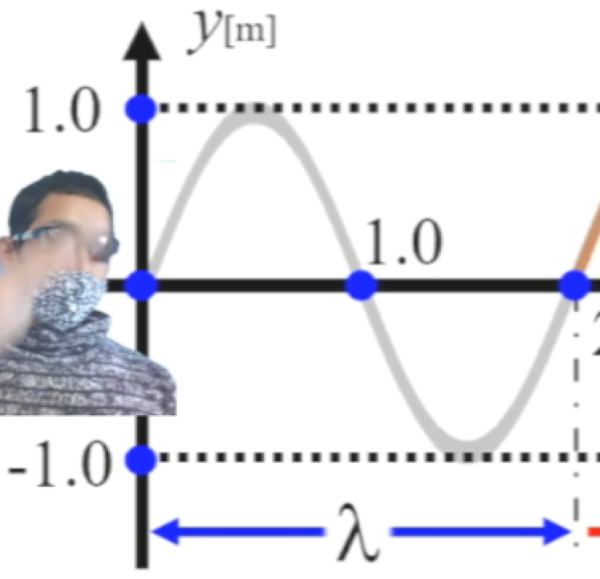
上下に振動するロープの振動が、どんどんどんどん伝わっていくんだよなぁ…。
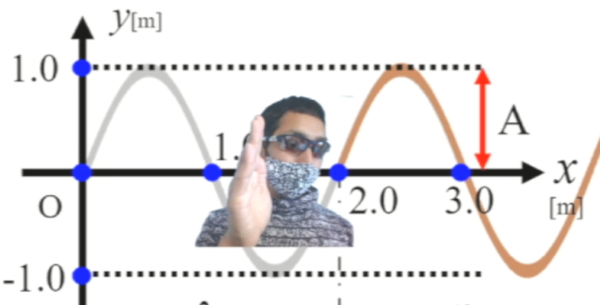

この2つの事やってほしいんです。
問題としては、波の振動が右向きに伝わっていくっていうのが、2番で最初に出てきました。
3番では、原点でロープを上下に動かすという考え方から、1回動かすと1つの波が出て行くという風に考えました。

どうしても問題用紙とか図とかそういう紙面上では、そのような動きがありません。

その動きを補って欲しいんです。
波動というのは、非常に単純な動き、それが伝わっていく様子というものを考えていく。ところが、紙の上で何かを議論しようとしたときには、動きが見えません。だから、まず与えられたものに対して動きが必要ない量。λや振幅。そういうものはしっかり押さえる。それ以外は、動きをしっかりと頭の中で想像してからそっから次のステップとして問題を解くということ。これを是非守っていただきたいと思います。


















