はじめに
前回に引き続き、波動に関する量について解説していきます。
■前回の記事

後のことは言ってみれば、「これ(λ=vtの式)を変形するだけ」と言っても過言ではありません。
それでは、次に波の振動数について考えていきます。
様々な物理量
振動数
一般にfrequencyの頭文字の f で表現します。
振動数というのは一体何なのかっていうと、
1秒間当たり何回振動しているか。
という議論になります。
1秒間当たりに何回振動するかというのを表す量が振動数です。

だから一体、振動数は
何のことを表しているの…?

それは、私の手の動きです。
ロープを揺らす手が1秒間あたりに何回振動するかというのが振動数です。


ということは…
これは1秒間当たり、何個の波を作っているを表わす量に等しい。
と言えることが分かってもらえるでしょうか?
試しに、1秒間にこれから2回振動させてみます。
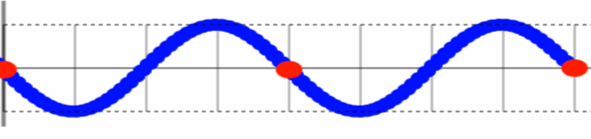
そうすると、1秒間に2つの波ができます。
だから「振動数が3ですよ」って言われたら、1秒間に3個の波作ります。
したがって、わかりやすく言うと、
振動数とは手の動きが1秒間当たり何回動いてるか
ということになります。

このように「簡単な言葉に置き換えて考えてみる!」ということも大切です。
振動数とは、1秒間当たり何回振動しているかという物理量です。
1秒間あたりという時間が関わってくるので、ここで周期Tとの関連性について見ていきます。
振動数と周期の関係
周期Tというのは、波1個分進むのに要した時間です。
波1個分進む間に、波は上下に1回振動します。

したがって、周期とは、1個の波を出すのにかかる時間とも言えます。
1個の波を出すのにT秒をかかります。
一方、波は1秒間にf回振動します。

つまり、1秒間にf 個の波が出ていきます。

そして、この式を解いてやると、次のようになります。
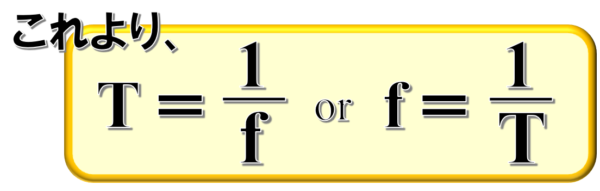
fとTは逆数の関係にあるということがわかります。

さて、それでは本題はここからです。
波の基本式
3番の波の伝わる速さのところで、λ=vTという式が1つ出てきました。
※波の伝わる速さについては前回の記事を確認してください。
それから周期と振動数の関係から、T=1/f という関係式が出てきました。
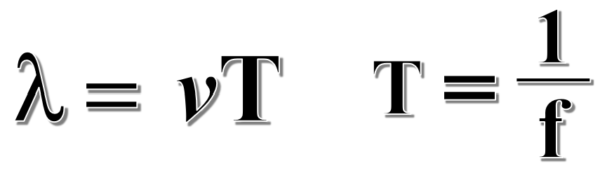
ということは、この2つの式からTを消去することができます。

そうすると、こんな式になります。

これは、波の基本式とも呼ばれる非常に重要な式です。

こうして、波の基本式について紹介したわけですが、忘れてはいけないことがあります。
それは、この式の和訳です。

皆さんは、この数式の意味を言葉で説明できますか?
1周期の間に進んだ距離、それはλに等しい。
がλ=vTの式でした。

こういう風に数式を言葉に置き換えることを和訳すると言います。
このように和訳できる。
λ=vTの式を変形して出てきた式が v=fλ です。

ということは、この式も何かしらの意味を持っていなければいけないはずです。
しかし、実際に和訳しようとすると、
振動数に波長をかけると速さに等しい。
1秒間あたり振動回数に波長をかけ算したら、波の伝わる速さになる。

というのは、意味がわからないですねぇ…。
だからと言って、「波の基本式とは、波の伝わる速さとは、振動数に波長かけたものという」浅い理解で終わって欲しくないところです。

v=fλは、波の基本式と呼ばれて、どんな波にでも成り立つ、とても便利な式なんです。

だから、この先、
しょっちゅう出てきます。
そのような大切な式を公式として記憶で誤魔化すことは得策ではないので、ゆっくりと考えていきます。

まずは速さについてです。
速さのままにしておくのは、かなり難しいので、両辺に1秒を掛けてみます。1秒かけます。
そうすると、これv(×1)は速さ×時間ということで、1秒間に進んだ距離ということになります。

だから左辺は、「1秒間にvだけ進みます」と言ってるんです。
次に右辺に移ります。

右辺に1秒を掛けると…

1秒間にf回振動する!
f 回振動する間に、f 個の波が出来るわけです。
そして、波1個あたりは λ という距離です。
だんだん見えてきました。
具体的に、振動数が2だとすると、1秒間に2個の波ができるということです。
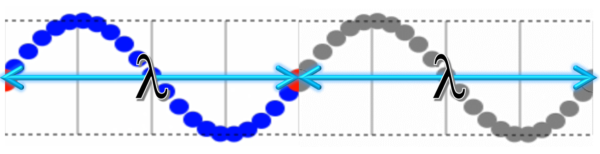
1秒間に2個の波ができる。1個2個。

つまり、波長が2個分です。

それが1秒間に進んだ距離に等しいはずだ!!
これでわかりました。

すごく重要な式なので、今みたいな和訳がちゃんとできることが大事です。
右辺は1秒間当たりに出している波の数です。

1個あたりλという距離なので、fλというのは、1秒間に進んだ距離に等しくなってるはずです。
そして右辺は、速さvに1秒間をかけるから1秒間に進んだ距離です。

振動数に波長をかけたら速さに等しいと言われても、それはよく分かりません。しかし、今のように例えば 1秒間に fλ だけ進んだんだ、という風に和訳をしてしまうと、この式を簡単に理解できるようになります。
すなわち、
1秒間に進んだ距離は、1秒間に出来る λ、f個分の長さに等しい。
という和訳になります。

両辺に1秒をかけてから和訳すると、v=fλという式が容易に理解できます。
位相、連続波、パルス波
これで、大切なことは全て伝えたのですが、後、少しだけ物理的な用語をまとめていきます。
今、図のような波があったとします。この時、こういうてっぺんの部分を山。
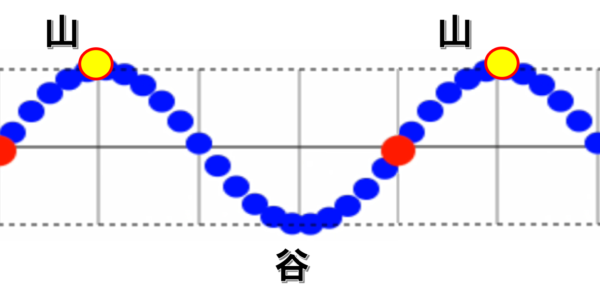
最下点のところを谷と呼びます。

それから難しい言葉があって、位置的相関と書いて位相(いそう)と言います。

例えば、こういう場所とこういう場所。
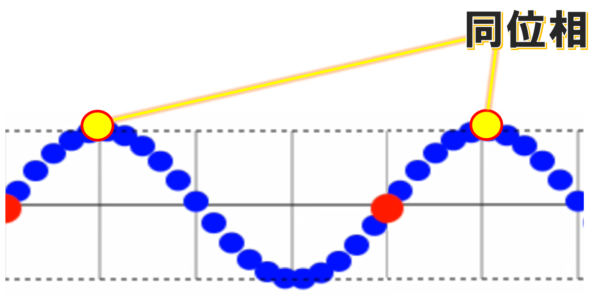

ここは言ってみれば、場所は違うんですが波としては同じような振動状態にあります。
そのような2点のことを同位相、もしくは位相が同じという言い方をします。
ですから、例えばここもそうです。
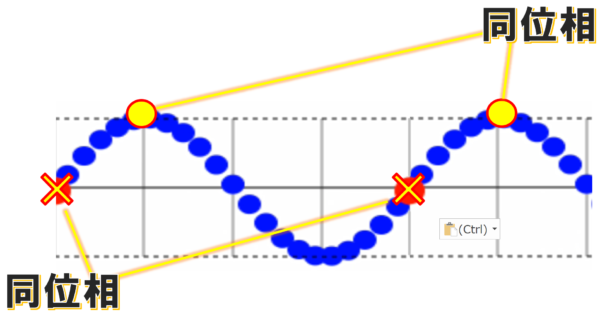
こことここ(×のところ)が同じ状態です。
これも同位相と呼んでいます。
それに対して、こういう場所は、今度は逆位相という言い方をします。

位置的相関が同じだから同位相。それに対して位置的相関が逆です。
というような言い方をします。
つまり、×と△の点では振動の状態が真逆の関係にあるということです。

×の位置のロープが上がっている時は、△のロープは下がり、逆に×が下がっていたら、△は上がる。
そのような真逆の関係にあるということです。

ですから、問題集を見ていると、「これと同位相の場所を言いなさい!」というような問題が出てきます。
そのような時は、位置的な周りの状況が全部同じところを言えばいいわけです。
それから
山と谷を比べると今度は逆位相
という言い方をします。

位相という言葉を聞くと、すごく難しく感じますが、「同」とか「逆」という文字が付いているおかげで、「一体何のことを言ってるのか?」ということは理解してもらえると思います。
それから、連続波とパルス波という言葉ですが、
連続波というのは、ずっと波源を動かしてると連続的に波が出ていく。このような波が連続波です。

パルス波というのは、1回だけピュッと行った波のことです。
波源から飛び出した一つの山がす~っと伝わっていく。
そのような波をパルス波と呼びます。
重要事項の確認/関連記事へのリンク
これで今回の講義パートは全て終わりました。
今回の解説の中できちんと押さえておいてほしいポイントを下のスライドにまとめました。
(答えは次のスライドの右下の赤字で示してあります。)

物理の学習ではきちんと用語や定義を押さえていかないと、内容理解が追いつかなくなってしまいます。
この記事の内容を始めて学習した方や、先々の内容があまり理解できないと感じる方は、一度基礎に戻って、専門用語や数式の内容を確認してください。
次回の記事では、ここで学習した基本事項を使いながら例題の解説を行っていきます。