目次
はじめに
前回の授業で仕事の原理について見ていきました。

そこでは、高さhのところに荷物を運ぶのに、直接hだけ持ち上げるのと、滑らかな斜面を使っても荷物にした仕事は同じであるということを学びました。
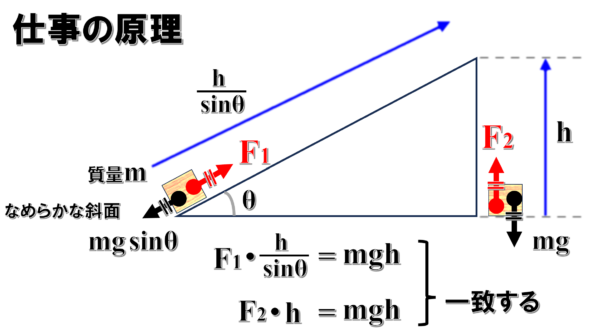
そして、このような場合であっても、力学的エネルギーは確かに保存されている。
つまり、斜面を登る前と登った後では力学的エネルギーは同じであるという事です。

これは、物体がどの位置にあっても力学的エネルギーが保存されるということを
意味しているのですが…
実は、力学的エネルギーが保存されない場合があります。
例えば、初速度v0で動く質量mの物体が、あらい面上を移動した場合、この面上を動く物体は摩擦力がはたらくことによって減速してやがて静止します。
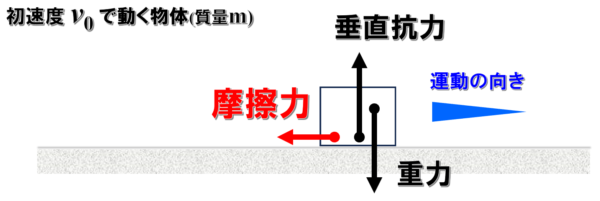

この時の前後の力学的エネルギーを考えてみます。
すると、運動エネルギーは、最初1/2mv02だったのが、後で静止するわけですから0になります。
一方、基準水平面での高さを0[m]とすると、位置エネルギーmghは、最初と最後で変わらず0のまま。
力学的エネルギーは、運動エネルギーと位置エネルギーの和ですから、1/2mv02から0に変化しています。
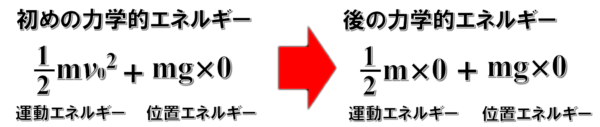
したがって、このような時は力学的エネルギーは保存されません。

この例からも分かる通り、力学的エネルギーは、きちんと保存されるときと保存されない時があります。
だから、「どのような時に力学的エネルギーが保存されて、どのような時に保存されないのか?」といった事をきちんと整理しておかないといけません。
保存力について
そこでもう一度、仕事の原理から遡って見ていこうと思うのですが・・・

仕事の原理というのは、荷物を高さh持ち上げるのに、直接持ち上げても斜面を使っても、トータルでの仕事量は変わらないということでした。
ここでは、逆になめらかな斜面上にある物体が斜面を下って基準水平面まで行く時に、重力がした仕事について考えてみます。
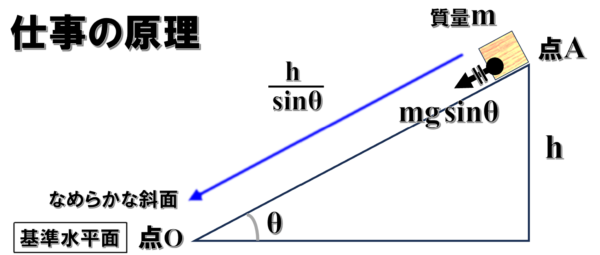
点Aから点0まで移動するとき
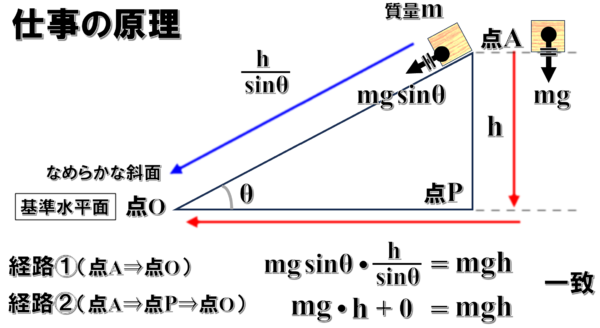
まずは、斜面上の点Aから基準水平面の点0まで移動するときですが、この時、質量mの物体は重力の斜面方向の成分mgsinθという力を受けて
sinθ分のhだけ移動します。
したがって、この時の仕事は、mgsinθ×sinθ分のhでmghです。
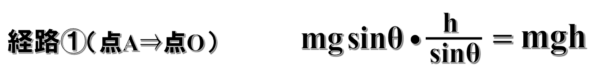
点Aから点Pを経由して点0まで移動するとき
次に、点Aから直接真下の基準水平面Pまで落ちてから点0まで移動する場合に移ります。
まず、点AからPまで移動するまでは、mgという重力を受けてhだけ移動するので、この時の仕事はmgh
点Pから点0まで移動することについては、移動方向に対して重力は垂直にはたらくので、この時の仕事は0です。
したがって、この時の仕事を合計してもmghとなります。
![]()
これが仕事の原理になる訳ですが…

このように、一般に物体が移動する時に物体にはたらく力のする仕事が、途中の経路に関係なく、始点と終点の位置だけで決まる場合、その力のことを保存力といいます。
この場合だと、重力は保存力であるという風に捉えることができます。
保存力は重力の他にも弾性力や静電気力があります。
力学的エネルギーが保存則の成立条件

実は、力学的エネルギーが保存される条件というのは、この保存力という力が関係しています。
きちんと整理しておくと、力学的エネルギーが保存されるのは…
「物体に保存力だけがはたらくとき」、または「保存力以外の力がはたらいても仕事をしないとき」だけである。
ということになります。
保存力以外の力がはたらいても仕事をしないというのは、例えば、先ほどの例では、斜面を下る物体には、重力の他に垂直抗力という力が作用しています。
垂直抗力は保存力ではありませんが、垂直抗力は斜面に対して垂直にはたらく力なので、斜面を下る時にした仕事は0。
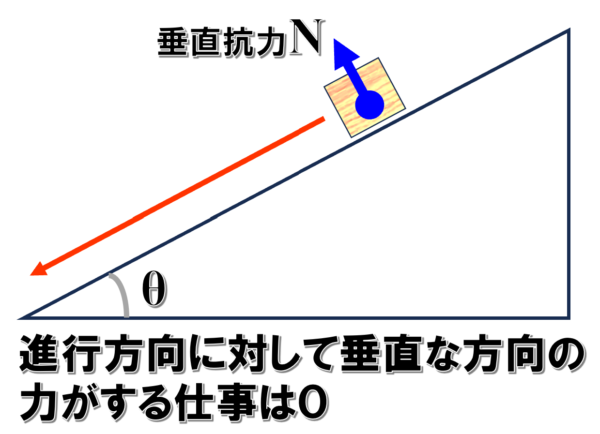
したがって、斜面を下るということに対しては、垂直抗力は仕事をしていません。
このような場合でも力学的エネルギーは保存されるということです。
保存力以外の力がする仕事
それから、力学的エネルギーが保存されない場合ですが、もしも、仮にこの斜面があらい面だったとします。
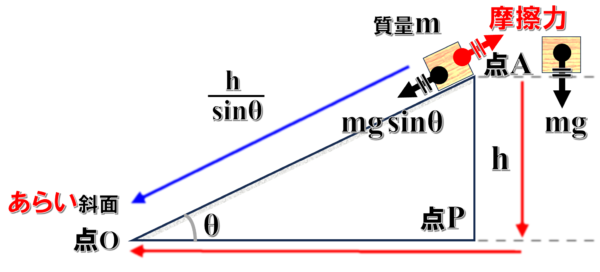
そうすると、斜面を下る時に摩擦力がはたらくわけですが、この摩擦力がした仕事は0ではありません。
この場合であれば、点Aと点0における力学的エネルギーは、摩擦力がした仕事の分だけ変化します。
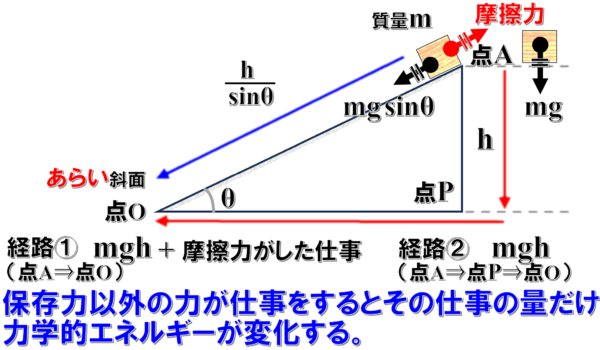
このような時は力学的エネルギーは保存されることはありません。

保存力以外の力が仕事をすると、その仕事の量だけ力学的エネルギーが変化します。
この場合だと摩擦力がした仕事の分だけ力学的エネルギーは変化します。
例題解説
そのことも踏まえて、例題を解いていきます。
水平面上の点Aを速さ1.4m/sで通過する質量1.0kgの物体がある。平面はなめらかだが、BC間のみ粗く、物体との間の動摩擦係数は0.15で、距離は0.50mである。重力加速度の大きさを9.8m/s2とする。
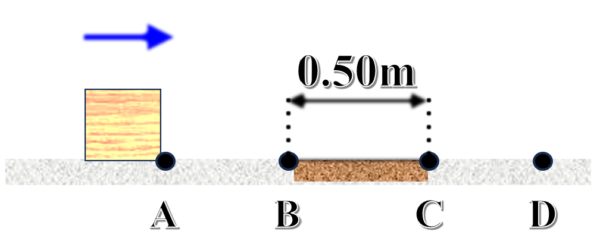
(1)物体がBC間を通過する間にされる仕事は何Jか。
まずは、BC間を通過する間の仕事です。

仕事は力×距離でBC間は0.50mです。
したがって、物体にはたらく力が分かれば仕事が求められます。
そこで物体にはたらく力を整理していくと…

物体には、地球からの重力、床からの垂直抗力、そしてあらい面を通過するので、動摩擦力がかかります。
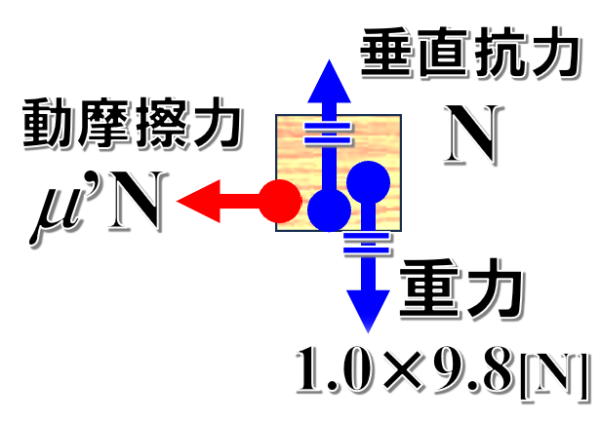
これから仕事について考えていくわけですが、

重力と垂直抗力については、進行方向に対して垂直にはたらく力ですから仕事は0です。
したがって、動摩擦力がした仕事だけを考えます。

そうすると、動摩擦力は垂直抗力を使ってμ’Nとかけるわけですが、μ’は問題文に0.15と与えられています。
それから垂直抗力ですが…、

ここの問題では、重力とつり合う力なので、1.0×9.8Nとなります。
従って、動摩擦力がした仕事をWとすると、Wは力×距離。

力は進行方向に対して逆向きにはたらくので、マイナスをつけます。
W=ー0.15×1.0×9.8×0.50
上の式を計算して、有効数字2桁に揃えると、答えはー0.74J(0.735)となります。
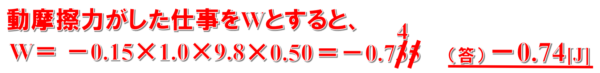
それでは次の問題に移ります。
(2)物体が点Dを通過する速さは何m/sか。
なめらかな平面を移動するのであれば、物体は等速直線運動します。(物体にはたらく力の合力が0のときは、慣性の法則に従います。)

この時、物体にはたらく力は重力と垂直抗力のみで、進行方向に対して垂直にはたらく力ですから仕事はしません。
この場合であれば力学的エネルギーは保存されるので、物体の運動エネルギーは変化しませんし、速さも一定です。

しかし、物体はBC間で摩擦力によって仕事をされています。
そのため、点Dを通過する速さは変化します。

ここでは点Aで速さ1.4m/sで通過した物体が、点Dを通過する時はどれくらいの速さになっているかと聞いているわけですが…
点Aを通過する時の運動能力が点Dでは変化している…

それは何故か??

BC間で仕事をされてからです。
したがって、ここでは仕事と運動エネルギーの関係を考えます。
点Dでの速さをvDとすると、
点Aでの運動エネルギーは、1/2×1.0×1.42
点Dでの運動エネルギーは、1/2×1.0×vD2
摩擦力がした仕事は、ー0.735
です。

物体の運動エネルギーは、最初は「1/2×1.0×1.42」だったけど、最後は「1/2×1.0×vD2」になりました。
それは、これだけ(ー0.735J)の仕事をされたからです。
こういう内容の式になります。
よって、これを計算すると、
vD2は、0.49
0.49は0.7の2乗ですから、vDは0.7となります。

【別解】力学的エネルギー保存則を用いて解く方法

ここでは仕事と運動エネルギーの関係式を利用して問題を解きましたが、力学的エネルギーの変化量が保存力以外の力がした仕事であると考えることもできます。
点Aでの力学的エネルギーは、運動エネルギーが1/2×1.0×1.42
位置エネルギーは水平面上を基準の高さとすると、mg×0で0
点Dの力学的エネルギーは、運動エネルギーが1/2×1.0×vD2
位置エネルギーは、0です。

点Aと点Dでの力学的エネルギーの差が保存力以外の力がした仕事、ここでは動摩擦力がした仕事であると考えて式を立てると、最終的には仕事と運動エネルギーの関係式と同じ式になります。

したがって、速さは0.7m/s

確かに保存力以外の力が仕事をするとその仕事の量だけ力学的エネルギーが変化することが確認できます。
このように考えて解くことも出来ます。
それでは今回の解説は以上とさせていただきます。















