はじめに
□前回の記事↓↓
単振動の解釈について
↑↑↑動画による解説はこちらをご確認ください。単振動と運動方程式
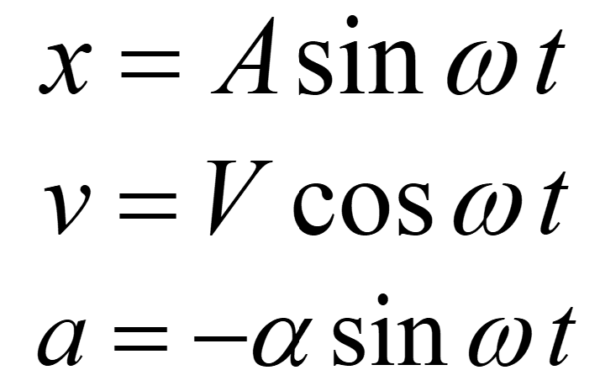

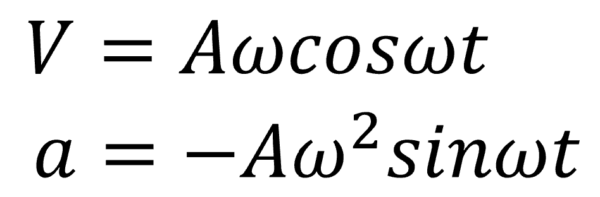

それでは、なぜニュートンはこんなことをやったのか??
まず、円運動の射影が単振動ではないだろうかという予想を立てて、このような量を求めていきました。

彼が本当に欲しかったのは、加速度なんです。
ニュートンには目的があったんです。

ということは、どう考えても加速度aはxに比例しないといけないんです。
だから、加速度aとxの間に何かしらの関係がないといけないわけです。ニュートンは場当たり的にやっているわけではないんです。

m a=Fという確固たるものがあるんです。
そして、実験で出てきたものと比べることによって、

加速度はxの関数として書けるはずだ!
そう思っていたわけです。

よ〜く見てください。
この3つの式を。
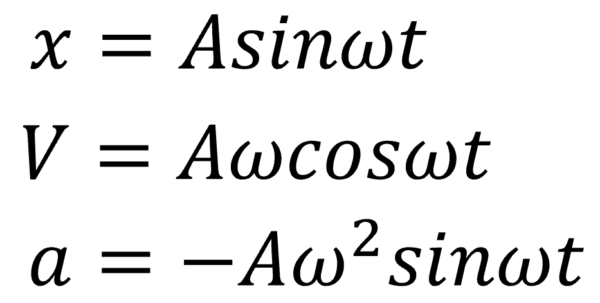
ここにA sinwtがあります。

A sinwt…

それはxです。
ということは、加速度aは…
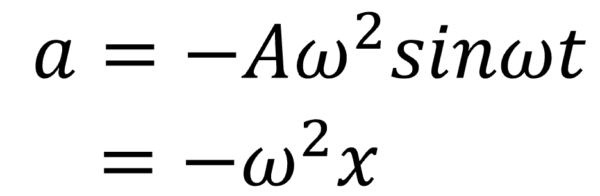

凄いですねぇ…
加速度aがxに比例しています。等速円運動ですからωは一定です。

これで上手く行きそうです。
では、これをニュートンの伝家の宝刀、運動方程式の中に代入すると、
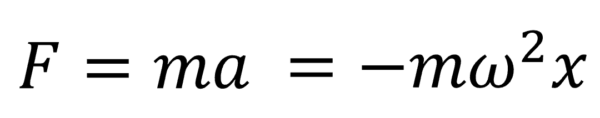

ということは、mω2を一つの文字に置き換えることが出来ます。
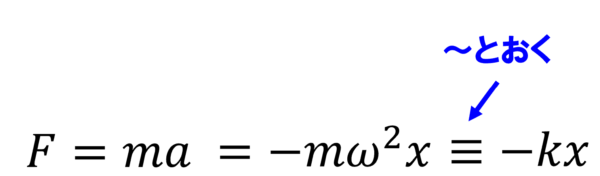
これで理論的に示すことが出来ました。

円運動の射影は単振動です。

なぜなら、物体に働く力が実験式と一致しているからです。
単振動の解析においては、ニュートンに軍配が上がりました。

その大きな理由として、このマイナスです。
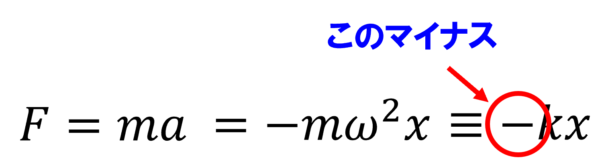

これが何を意味するの?
バネは、グッと縮めれば伸びたくなります。グゥっと伸ばせば縮みたくなります。必ず変位と逆向きになるんです。フックもその事にはわかっていたはずです。

ニュートンは、そのことをこの式で見事に導き、マイナスがつくということをごくごく自然な幾何学だけを使って示しました。
ただ三角形のサインとかコサインを利用することによって、ニュートンは実験式を理論的に導くことに成功しました。こうして、単振動というのは、円運動の射影であるということを突き止めることに成功したわけです。もうこれは、天才であるとしか言いようがありません。
しかし、ここにはm a=Fという伝家の宝刀があり、さらにフックがF=kxを示し、

じゃあ加速度aはxに比例しなければならない…
という手近なゴールがあったわけです。だから、ニュートンは、このような数式の運用を行なったわけです。

教科書を見ていると、こうした歴史的背景が抜けていることがあります。
そうすると、数式の羅列だけになってしまって、

なるほど…
とは思いますが、それだけだと物理が面白くなくなってしまうんです。
だから、変位x、速度v、加速度aを数式にして、

やっぱり加速度の中にxがあるじゃないか!
ということを示したわけです。
たまたま気付いたわけではないんです。
目的を持っていたんです。

円運動では加速度がrω2乗とかけるのと同じように、単振動ではーω2xとかけるんです。とても大切です。
単振動と微分・積分の話

まず変位xですが、xの式をtで微分するとどうなりますか?
ωが前に出て、 サインがコサインに変わります。そうしたら、Aωcosωt…。ちゃんとvになっています。
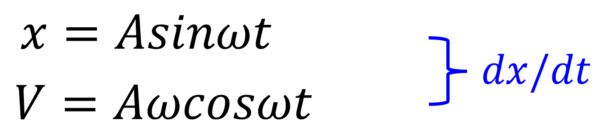

時間で微分するということは、時間に対する変化量を求めるということです。
時間に対して、xがどれくらい変わったか??
と言われたら、それは速さのことを聞いてるわけです。つまり、変位xを時間tで微分したら速度vになります。

それでは、もう一度行きます。
次は速度vをtで微分します。そうすると、wが前に出て、コサインがマイナスサインに変わります。
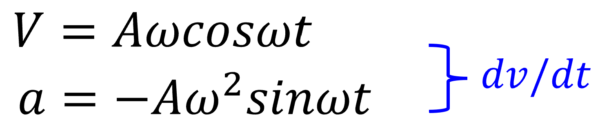

速度vを時間tで微分する…。
つまり速度の単位時間あたりの変化量を求めるわけですから、それは加速度になります。

この話は参考程度に聞いといてもらえば十分なのですが…
そもそも1番最初に微分とか積分を考え出したのはニュートンです。ある朝突然、目が覚めた時に微分積分を閃いたわけではないんです。物理学的に数式の運用をしていったときに、vはxの変化量でなければならないとか、 aはvの変化量でなければならない。そういったところから、このような事(v=dx/dt、a=dv/dt)に気付いていったわけです。

確かにニュートンは天才だと思いますが、だからといって何もしないで頭の中で何かが閃いたというわけではなくて、何らかの目的に向かって試行錯誤している内に、1つの結論に辿り着いていったわけです。
円運動と単振動の類似性になぜ気付いた??
それでは、再び単振動の話に移ります。

ところで、ニュートンはなぜ円運動と単振動の類似性に気付いたのでしょうか??
そもそも、円運動は回る運動で単振動は前後に行ったり来たりする運動です。パッと見ただけでは、そこに類似性がある事にはなかなか気付けなかったと思います。

そこでまず単振動がどういった運動なのかを考えてみます。
単振動は等速円運動の射影だと言いました。等速円運動は、中心方向に落ち込みならがグルグル回る運動です。単振動はその射影運動で、円に光をあてた陰の運動に相当するわけです。その陰は、ちょうど円をギュッと1本の棒のように圧縮したようなものです。そうすると、円周を回る物体の運動は常に中心に向かう運動になります。


円運動を射影しただけなので、意味がついてくるんです。
つまり、単振動の加速度は、「振動中心に落ち込む」という意味になります。


さて、そこで、なぜニュートンが円運動と単振動の類似性に気付くことが出来たのか?
それは、運動の意味が同じだからです。
円の中心方向に落ち込む、これが円運動
振動の中心に落ち込む、これが単振動です。
ニュートンはただ単に数式を使って、やみくもに導出していたわけではありません。必ず頭の中で数式を意味としてとらえていたわけです。単なる数字と記号の羅列ではなくて、確かに加速度がr分のv2とかrω2と書けるけども、それで満足していなんです。

そうやって表現できる加速度にはどんな意味があるのか??
そのように考えていったわけです。

それが物理学です。
確かに物理学においても、実験的手法は大切です。しかし、それでは実験だけで十分なのかというとそんなことはありません。理論が重要です。数式が大切です。かと言って、数式だけで良いのかというと、そうでもありません。意味がわからないといけません。そうでないと、数式の使いどころがわかりませんし新たな発見もありません。

したがって、物理学の面白さというのは、「実験で起きることと理論で考えたことが一致することにある!」と言っても過言ではありません。
このような学問的魅力に触発されて物理学が発展してきたと考えると、単に公式を覚えて数式を立てて終わりにしてしまっては面白くもないですし、数式の意味がわからないと、未知の問題に対して全く手が付けられなくなってしまいます。