
はじめに
前回の記事で運動方程式について解説したので、今回はいくつか問題を解いていきます。
基本問題解説
(2)解説
(2)なめらかな床の上に、質量がm1、m2の物体が軽い糸でつながれて置いてある。質量m1の物体を水平方向に大きさFの力で引いたとき、これらの物体に生じる加速度と糸の張力の大きさを求めよ。
※(1)の解説は前回の記事を参考にしてください。
まず図で状況を整理していきます。
糸でつながれた2つの物体があり、質量m1の物体は大きさFの力で引かれます。床はなめらかで摩擦力がはたらかないので物体は力の方向に動き始めます。このときの加速度をaとします。
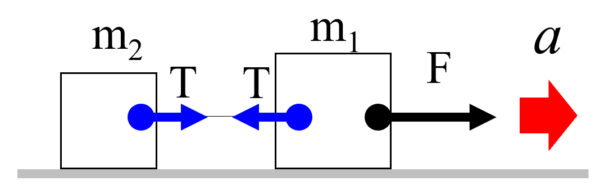
そして、この時、質量m2の物体を引く力はFではないので注意してください。物体にはたらく力は、「場の力」と「接触力」の2種類だけです。基本的に重力以外は接触力になります。質量m2の物体は接触力である糸の張力Tによって引かれます。

糸がなければ、この物体は動かないはずです。
力Fは、この物体には接触していません。この糸の張力Tは、m1の物体を引っ張った反動によって生じると考えると、m1の物体には逆向きに大きさTの張力が糸からはたらきます。
したがって、それぞれの物体に対して運動方程式を考えると、

![]()

![]()
この2つの式を連立して、加速度aと張力Tを求めます。①式と②式の左辺同士、右辺同士を足し算します。
そうすると、加速度aと糸の張力Tは次のようになります。
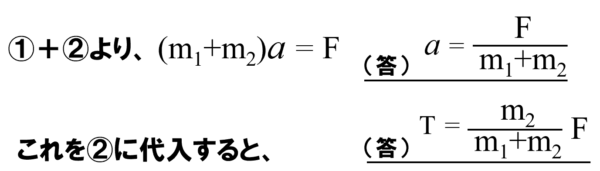
これで解答は終了しましたが、途中計算に出てきた①式プラス②式について、もう少し考えてみます。この式は、2つの運動方程式を足したものですから、この式も何らかの因果関係を示す式になっているはずです。
そこで、この式を日本語に和訳してみると、
m1とm2の物体に加速度aが生じたのは、力Fがはたらいたためである。
と解釈することができます。
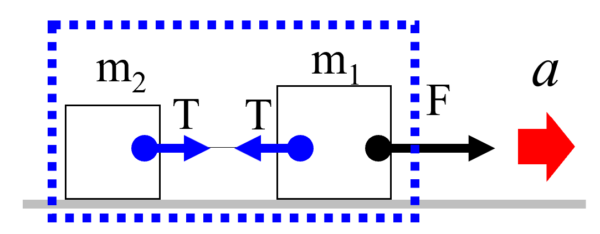
つまり①式②式の和は、2物体をひとまとめにして、「2物体に加速度aが生じたのは、力Fである」という因果関係を示す式です。

このように自分自身が立てた式の意味を理解して問題を解き進めていくと、計算ミスなど、手痛い失点を防ぐことが出来ます。
それでは次の問題に移ります。
(3)解説
(3)傾斜角q のなめらかな斜面上に質量mの物体を置くと、物体は斜面を滑り降りた。このとき物体に生じる加速度の大きさを求めよ。
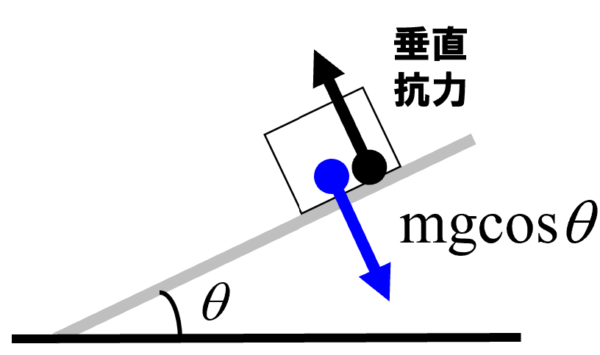
なめらかな斜面とあるので、物体には摩擦力ははたらきません。
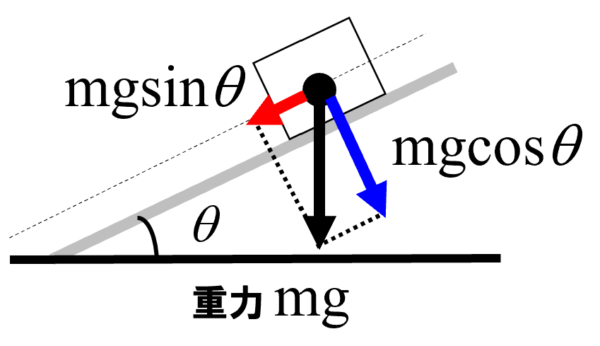
この時、物体は重力の斜面方向の成分mgsinq によって、斜面を滑り降ります。重力の斜面に垂直な成分mgcosq は、垂直抗力とつり合っているので、この力によって物体の運動状態は変化しません。
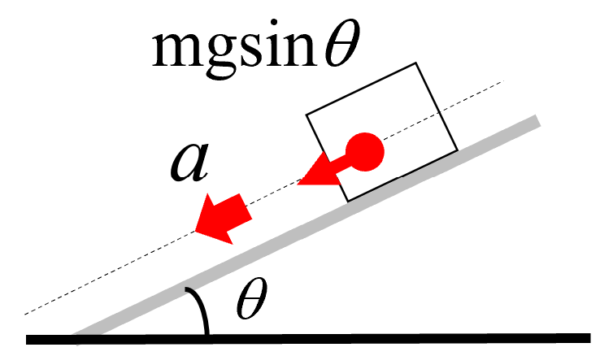
斜面方向の運動方程式を立てると、
質量m[kg]の物体に加速度aを生じさせたのは、重力の斜面方向の成分、mgsinq が作用したからである。
これより、加速度aを求めるとgsinq となります。
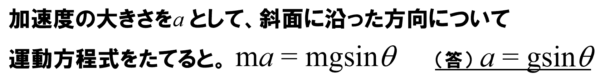
sinq かcosq で迷った時は…?
ここで力の分解について補足しておきます。今、重力の斜面方向の成分をmgsinqと定めましたが、最初の内は、sinq なのかcosq なのかの判別が難しく感じると思います。そのような時は、角度の連続性に着目してください。
たとえば斜面の傾斜角度q がだんだんゼロに近付いていくことを想像してみます。
重力は、地球の中心、つまり平面に対して垂直にはたらく力ですから、斜面が徐々に平らになっていくと、重力の斜面方向の成分は0に近付いていきます。
それに対して、重力の鉛直方向の成分は、mgに近付きます。
この時の状況をmgsinq とmgcosq が満たしているかを考えると、mgsin0は0 、mgcosq はmgですから、斜面方向と鉛直方向の力の分解が正しく行われていることが確認できます。

問題の解説は以上です。

初めて物理を学習する人にとっては、ここからの学習内容が一気に高度になったように感じられたのではないでしょうか ??
高校物理では、今回学習した運動方程式を基礎として、これから仕事とエネルギーの関係や運動量といった発展的な内容が展開されていきますので、運動方程式の理解は必須となります。

高校物理の中で最も重要な単元であると言っても過言ではありませんので、もしも今回の授業で苦手意識を抱いた人は、教科書や参考書などにも目を通して理解を深めていってください。
それでは、今日の授業は以上となります。お疲れ様でした。














