
はじめに
今回は、運動方程式について学習します。

運動方程式は、ニュートンの運動の法則における第2法則に名を連ねています。
第1法則が慣性の法則、第3法則は作用・反作用の法則になるわけですが、これについては、以前の授業でお伝えしたので、今回は第2法則の運動方程式に焦点を当てて解説していきます。
運動の法則
この運動方程式は、何のための式なのかというになりますが…

第3回目の講義で慣性の法則について、学習しました。
慣性の法則とは、物体にはたらく力がつり合っていれば、その物体は静止しているか等速直線運動するということでした。

それでは、物体にはたらく力がつり合っていなければどうなるのか?
ということで、慣性の法則に続く内容として、運動方程式が登場します。
1.運動方程式の特徴
運動方程式は、高校で学習する物理の中で最も大切な式であり、ma=Fという非常にシンプルな表記をもちます。


この式を見れば、力Fに関わる式であるということがわかります。
一般的に運動というと、我々の感覚だと動いているもの、つまり速度に着目するところです。しかし、運動方程式では速度ではなくて加速度に着目しているところが特徴的です。
そこで、運動方程式を加速度aイコールの形に変形してみます。
すると、物体にはたらく力がつり合っていない時、加速度が生じるということでしたが、
加える力が2倍、3倍となると、その時生じる加速度も2倍、3倍となっていく。

つまり物体に生じる加速度は、物体にはたらく力に比例するということがわかります。
一方で、物体の質量が2倍、3倍となると、その時、生じる加速度は2分の1、3分の1となることから、

物体に生じる加速度は、質量に反比例することがわかります。

物体に生じる加速度は、力に比例して質量に反比例するということは、実験的に導かれた事実です。
そこから、数式の運用を効率化するために、
質量1[kg]の物体に1[m/s2]の加速度が生じるときに、はたらいている力が1[N]である!!
として、新たな力の単位を導入しました。

こうしてできた式ma=Fが運動方程式。ニュートンの運動の第2法則になります。
2.運動方程式の使い方
それでは、今から例題を用いて運動方程式の使い方を確認していきます。
(1)なめらかな床の上で、質量5.0kgの物体を前方に20N、後方に10Nで引いた。このときに物体に生じる加速度の大きさを求めよ。
水平方向にはたらく力を整理すると、前方に20N、後方に10Nの力がはたらいています。床はなめらかなので、摩擦力ははたらきません。この時、前後の力はつり合っていないので、物体には加速度が発生します。
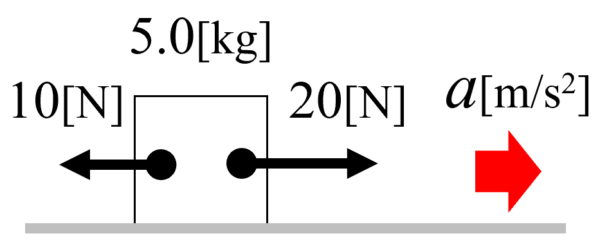
前方を正の向きとして、物体に生じる加速度をa[m/s2]とします。
そうすると、運動方程式は次のよう表現できます。
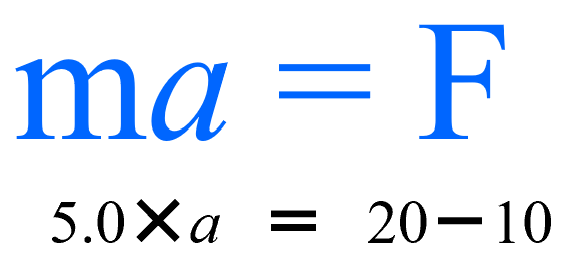
質量5.0kgの物体に、加速度aを生じさせたのは、前方に20Nの力と後方に10Nの力の合力が作用するためである。
という意味の式になります。これより、加速度aは2.0[m/s2]となります。


ここで、とても大切なことを確認します。
第1回目の講義で、物理では言葉の代わりに数式を使ってコミュニケーションすると伝えました。これは、数式をただの数字や記号の羅列として扱うのではなく、日常会話で使う言葉と同じく、意味をもったものとして正しく解釈しないといけないということです。
今回学習した「運動方程式は因果関係を示す式」になります。
例えば今回の問題では、鉛直方向には重力と垂直抗力がはたらきます。この2力はつり合っています。これを数式で表現する場合は、重力=垂直抗力として、「重力と垂直抗力は等しい」と数式から読み取ります。
一方で、運動方程式については、質量×加速度が力に等しいと解釈するのではなく、
「質量m[kg]の物体に加速度a[m/s2]を生じさせたのは、物体にはたらく合力F[N]の力である。」
と、
物体にはたらく力の合力という原因によって、物体には加速度が生じるという結果になった!
と解釈をします。

これを因果関係といいます。
回りくどい話になりますが、maに等しい力は何だろうかと、ma=Fの式に、適当な力を当てはめようとすると人と、こういう力がはたらいているから、物体には加速度が生じるはずだと、理論立てて考えられる人では、この先、物理の実力に大きな差が生まれてきます。

次回は運動方程式の問題をいくつか解いていきますが、その時も物体にはたらく力とそれによって生じる加速度の因果関係を意識しながら理解するように心がけて行ってください。















