
目次
はじめに
ゼロから学ぶ高校物理基礎ということで早速授業を始めていきます。
この講座では、文字通り、高校で物理基礎や物理を学習していない人を対象に、高校物理の基本事項を効率よく学習していきます。もしも、講義を聴いていて不明な点がありましたら、コメント欄に質問してください。それでは早速始めていきます。
2.速度とは、単位時間あたりの位置の変化、加速度とは、単位時間あたりの速度変化である。
3.等加速度運動の式はv-tグラフから導かれる。
1:物理学とは
それでは、まず1つ目の物理では、どういった事を学習するのかということですが、
ウィキペディアの内容を抜粋してみました。
 重要なところを色付きにしたので、そこのところを見ていくと、
重要なところを色付きにしたので、そこのところを見ていくと、
物理学は、自然界の現象とその性質を、物質とその間に働く相互作用によって理解すること(力学的理解)、および物質をより基本的な要素に還元して理解すること(原子論的理解)を目的とする。
ということですが、高校で学習する範囲では、赤字の力学的理解が中心となります。

そして、数学との親和性が非常に強い。
というのが物理学の特徴です。
そして、今後学習するテーマとしては、物体の運動とか光、音、電気と磁気、熱、波、天体の物理現象が中心となります。
それから
物理学では、理論やモデルを数式として表現することが多い。これは、自然言語で記述するとどうしても厳密さに欠け、定量的な評価や複雑な推論をすることが難しいためである。
とあるのですが、具体的にどういったことかを説明していきます。

例えば、「足が速い!」という言葉を聞いたときに、今、頭の中でどういったものを連想しましたか?
足が速いと言われれば、それは、
クラスで足が速い人(陸上部)であったり、

はたまたオリンピックの金メダリストだったり、

そもそも人ではなくて野生のチーターなど、

想像する人によってさまざまなものが思い浮かんだと思います。
それで、この時に問題になってくるのは、足が速いといっても、クラスの陸上部では、とても金メダリストの足の速さにはかなわないだろうし、そんな金メダリストであっても、野生動物にはかないません。

こうして、足の速さを議論する時に、人によってバラバラなことを想像してしまうと、話が噛み合わないことがあります。金メダリストは足が速いと思う人がいる一方で、いや、野生のチーターよりは遅いだろうと考える人がいる。

このように言葉による表現は、個人によって認識のずれが生じてしまうことがあります。
そこで、物理学では、こういった不具合を解消するために数式を活用していきます。
例えば、速さは、小学校で距離÷時間と教わってきたと思います。
これは何をやっているのかというと、ある地点から別のある地点までの距離をどれだけ早く進んだかを、到達するまでに要した時間を使って計算しているわけです。
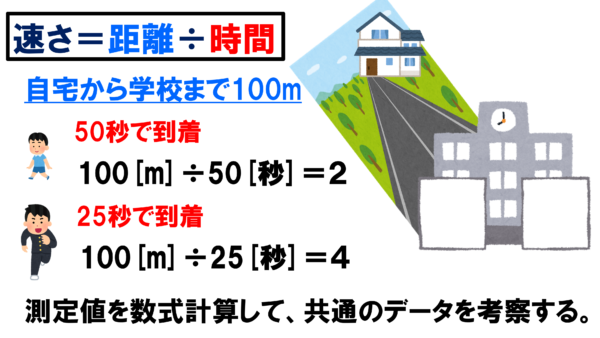
家から学校まで100mの道のりを50秒で到着する人と、25秒で到着する人であれば、25秒で到達する人の方が速いことがわかります。この時の速さを数式で表現すると、100÷50=2と100÷25=4で、速さ2よりも速さ4の方が大きい。
ということで、

速さの優劣を2と4という数字の大小関係で比較することができます。
こうして、距離や時間という共通のものさしによる測定値と、数式によって導かれた計算結果によって、個人の感覚に左右されること無く速さについて議論ができます。
つまり、
物理学は言葉の代わりに、数式を使ってコミュニケーションするための学問である
とも言えます。
物理学についての話は大体終わりになりますが、

この先、注意しないといけないことがあります。
速さ2とか4という数字には、意味がないので100mを50秒で到達した速さは、100÷50つまり100mを50等分して、1秒間に2m進む速さを表したものであるということを伝えないといけません。

100÷50=2という数字の羅列だけだと、それが一体何の数字なのかがわかりません。
だから、こういうときは、2[m/s](=メートル毎秒)、4[m/s]と単位をつけます。

物理学では、数字の後ろに単位をつけて、それが、何を表している数字なのかが理解できるようになっています。
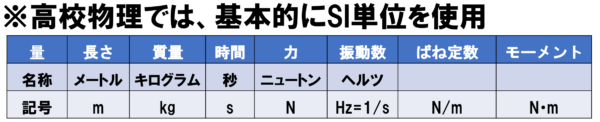
高校物理では、SI単位を基本的に使用するので、今後はSI単位を基準に講義を進めていきます。
※速さと等速直線運動についてより詳しく学習したい人は、次の記事を参考にしてください。
要点だけを効率よく学習したい人は、次の「2:速度と加速度」に進んでください。
2:速度と加速度
それでは早速、速度と加速度について説明します。
速度について
まずは、言葉による定義ですが、

速度とは、「単位時間当たりの位置の変化」のことを指します。

単位時間とは、1秒間とか1分間とか、1を基本にした時間のことです。
位置の変化とは、進んだ距離のことを指す表現になりますが、もう一つ重要な意味を含んでいます。

それは、物体が進んだのか後退したのかということです。
例えば5m前進したのであれば、位置の変化は+5m、後退したのであれば、位置の変化は-5mとなります。

従って、
2秒間に5m前進したのであれば、速度は2.5[m/s]
2秒間に5m後退したのであれば、-2.5[m/s]
とします。

ここまでの説明を数式で表現すると次のようになります。

Vとはvelocityの略語で速度とか速さの意味で用います。
Δxが位置の変化量、Δtが時間の変化量になります。
Δ(デルタ)とは変化量を意味する記号で、物体が動き出してから2秒間に5m前進したのであれば、最初の位置(0m)から5mだけ位置が変化したということで、Δxは5m、かかった時間、つまり変化した時間は2秒だから、Δtは2秒となります。

初めて数式をみると、「何のことかさっぱり」といった感じですが、慣れてくるとこちらの方がシンプルな表現で大変重宝します。
ちなみに物理では、速度の大きさを「速さ」として区別しています。つまり、前に進んだか後ろに進んだかではなくて、単純に進んだ距離(長さ)を時間で割ったものが速さです。
※速度と変位について、もう少し詳しく学習したい人は、次の記事に進んでください。
※平均・瞬間の速度、速度の合成、相対速度について詳しく学習したい人は、次の記事に進んでください。
加速度について
それでは次に加速度です。
加速度とは、単位時間当たりの速度の変化のことを指します。
数式で表現すると、こうなります。

Δvは、速度の変化量のことで、速度が上昇すれば、Δvは正の数となり、加速することを意味していて、速度が減少すれば、Δvは負の数となり、減速することを意味します。

例えば秒速10メートルで走っていた車の速度が2秒後に秒速15メートルになっていたら、速度の変化量はvはプラス5なので、加速度は、2.5、単位は[m/s2]と書いてメートル毎秒毎秒と言います。
※加速度について詳しく学習したい人は、次の記事に進んでください。
3:等加速度運動
それでは、今から、実際に加速度運動する物体の運動について考えていくわけですが、ここでは一定の加速度で運動する物体の等加速度運動を中心に取り扱っていきます。
等加速度運動には、次に示す3つの式があります。

等加速度運動する物体について考える時には、この3つの式を利用するわけですが、その前に、これらの式がどのようにして成立しているのかを確認していきます。
等加速度運動の式とv-tグラフ
等加速度運動の式を理解するために、これからv-tグラフを作図します。
v-tグラフというのは、速度vと時間tの関係をグラフに表したもので、皆さんが数学の時間に1次関数や2次関数の式を横軸にx座標、縦軸をy座標としてグラフに表現するものと同じです。
v-tグラフでは、縦軸に速度vをとり、横軸に時間tをとります。
それでは、例として、次のような状況を考えてみましょう。
まず、一定の速度v0で動く物体があります。この物体がt秒間移動してx0[m]の位置を通過します。その後、物体は加速度a で t 秒間加速して、速度が v [m/s]になったとします。この時、進んだ距離をx [m]とします。
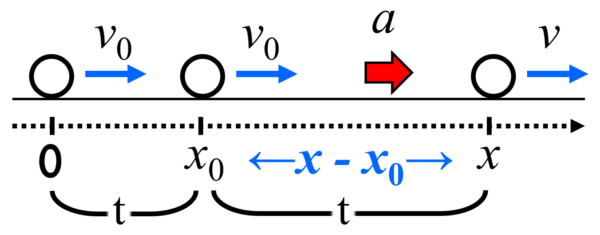

文字による表現が最初のうちは慣れないと思いますが、その時は、適当な数字をイメージしながら学習してください。
それでは今から、この状況をv-tグラフに書き込んでいきます。
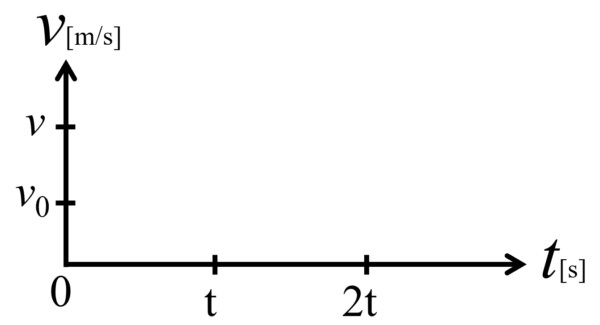
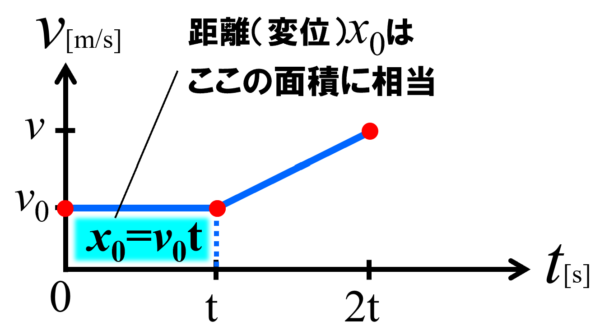
まず、最初のt秒間は、速度が一定だったので、時刻0と時刻tの時、速度はv0 。従って、v0 の位置に2つ点をグラフに打ちます。
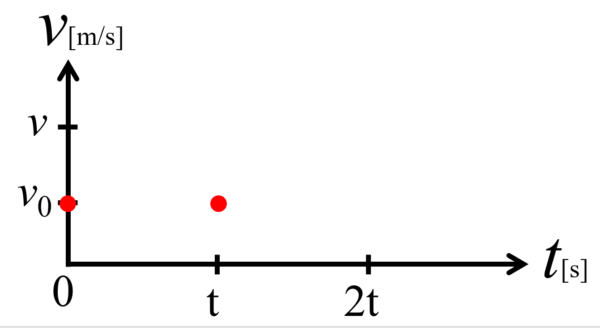
この2点を結ぶと、物体が一定の速度 v0 でt秒間移動したというグラフが完成します。
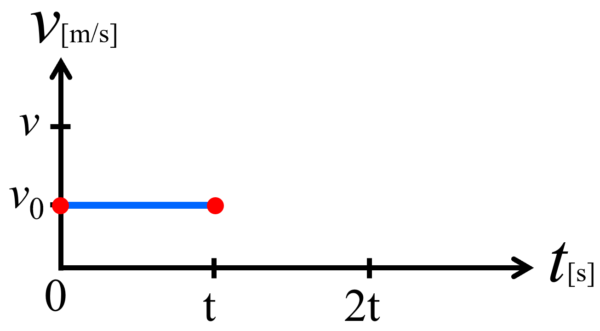
この時の移動距離に相当する x0 は、速さ×時間、厳密には速度×時間と言った方が正確ですが、これを計算すると、x0 はv0×t となります。v-tグラフ上では、v0×t というのは、縦 v0 、横 t で囲まれたこの四角形の面積に相当します。
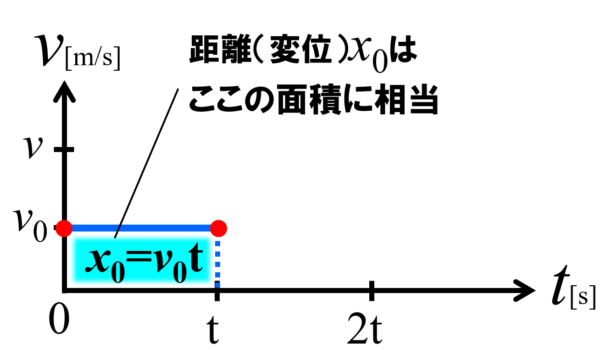
次のt秒間ですが、ここでは一定の加速度aで速度が変化します。t秒後の速度がvですから、時刻2tの位置で、速度vとなる点を打ちます。
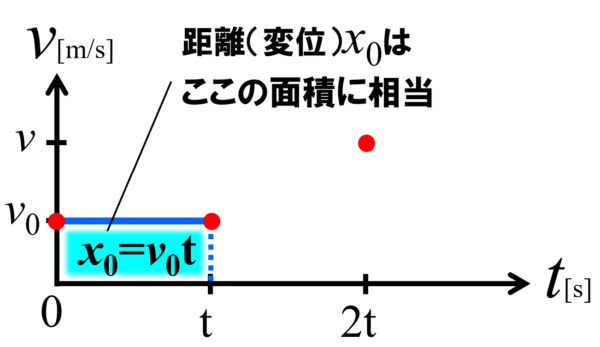
そして、時刻tの点と時刻2tの点を結びます。
加速度とは単位時間当たりの速度変化、ここでは1秒間あたり、速度がaだけ変化するということですから、t秒間だと、速度は a の t 倍の at だけ変化したことになります。最初の速度が v0 だったわけですから、速度 v はv0 + at と書くことが出来ます。
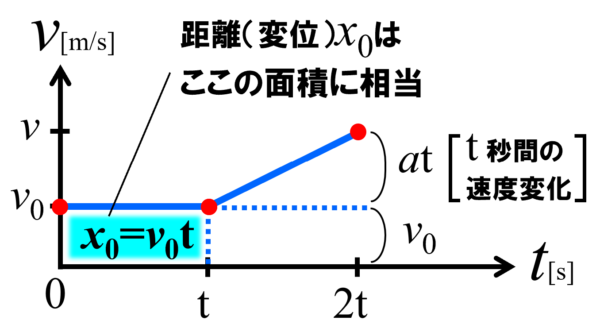
この関係式が、等加速度運動の1つ目の式になります。
等加速度運動の2つ目の式の導出
この間の移動距離は x0 からxまでなので、x-x0 となりますが、速度が刻一刻と変化しているので、先ほどのように、x-x0=v0t とか vt という単純な計算では求まりません。
これについて、先ほどのグラフの直線に囲まれた部分が移動距離に相当するという結論から考えてみると、この台形部分の面積がx-x0 に相当するのではないかという推測が出来ます。本来であれば、もう少し厳密に議論するべきところですが、ここでは省略します。
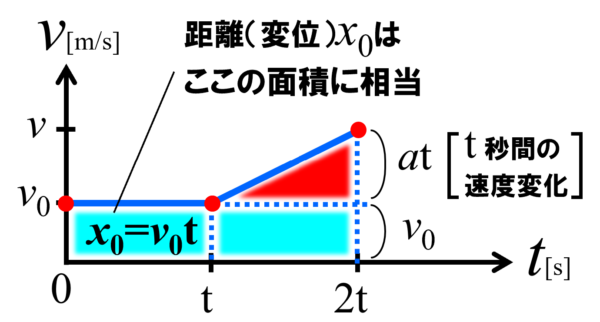
この推測より、台形部分の面積を求めてみます。この四角形の部分は先ほど v0t であることを計算で求めたので、三角形の部分を計算すると、横が t で縦が at の三角形ですから、1/2at×tで1/2at2となります。
これをまとめると、次のようになります。
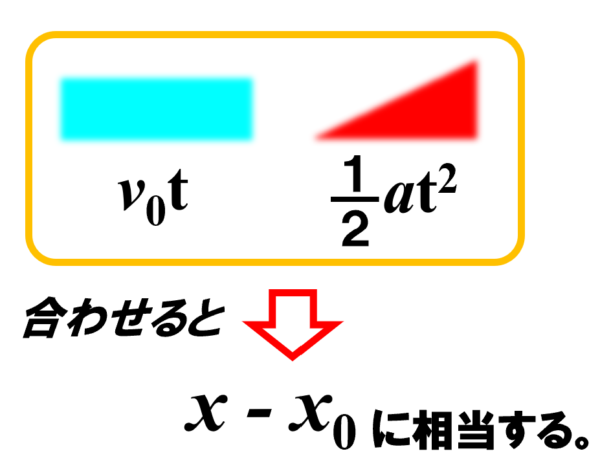
これが、等加速度運動の2つ目の式になります。
等加速度運動の3つ目の式の導出
そして、今導いた2つの式からtを消去すると、3つ目の式が導かれます。
一度、自分の手で計算してみて、正しいかどうか確かめてみてください。
これで等加速度運動の3つの式が導かれました。2つ目の式ですが、先ほどの説明では、最初の位置をx0としていましたが、x0 を原点、つまり x0 = 0 として、表現してあるので注意してください。実際の問題を解く時は、この式の形の方が、使いやすいです。
※等加速度運動の式を使った計算を具体的に確認した人は、次の記事に進んでください。
□等加速度運動の問題解説記事はこちら




















