はじめに

単振動というと、ばねの先におもりがついていて、それが揺れる様子というか、振動する様子を考えていくんですが…
実は、その単振動現象というのは、必ずしも「ばね」だけではありません。ちょっと想像してみてください。


それをちょっと沈めて、パッと手を離すと「びょ~んびょ~んびょ~ん」となります。
これは実際には減衰振動と言って、振動する度にだんだんと振幅が小さくなっていく振動ですが、そのような振動もあるわけです。実際過去の入試問題では、そのような問題が出題されたこともあります。

しかし、全ての基礎は、ばねの先におもりがついている場合です。その場合についてちゃんとした理解が出来ていれば、見たことがない振動の問題を解けるようになります。
したがって、今回の講義では、ばねに対して、どのようなふるまいをするのかを見ていきます。
単振動の基礎①(変位x、速度v、加速度a)

ばねというものが学問上皆さんの前に登場するのは、小学校の頃だったと思います。
その頃は、まだ正式な名前は教わらなくても小学校でフックの法則F=kxという、ばねの伸びや縮みに比例した力が働く力を教わっていると思います。

このF=kxっていうのはフックによる発見であったわけですが…
化学の範囲だったと思います。

ボイルという人をご存知でしょうか?
熱力学の世界にボイル・シャルルの法則があります。そのボイルの方です。

実は、そのボイルとフックとは、友人関係にあって、共同研究をやっていました。

ある時に、このボイルが閉じ込められた気体に対してピストンを「ぎゅ~っ」と抑え込むという事をやっていました。
ぎゅ~っと抑え込むと、体積が小さくなる。しかし、圧力は上がる。温度が一定ではpVが一定である。圧力と体積を掛けたものが一定である。これがボイルの法則です。

それを発見したわけです。

実は、その研究をやっている時、かたわらにフックがいました。ところが、そのフックの目の付け所が、ボイルとは違っていたんです。

フックは、そのボイルが押さえていた手を、放した時にどうなるか…??
という所に着目していたんです。

その時、ピストンが「びゅ~んびゅ~んびゅ~ん」ってなったんです。
これがいわゆる空気ばねです。現在は、車とかバイクとかのエアーサスペンションに使われている空気ばねです。


しかし、人は称賛されると時として慢心してしまいます。
要は少し天狗になってしまったということです。そのために、力学の分野では後にニュートンに追い抜かされてしまって、今では、フックとニュートンを比べると、ニュートンの方が有名であるということは、ご存知のことだと思います。


あっ、ばねのね!?
っていう。
フックは、さまざまな研究をやってきたわけですが、単振動に関して言うとフックはニュートンの影に隠れてしまいました。

しかし、なぜ陰に隠れてしまったのでしょうか…?
そのあたりも説明の中で分かってくると思います。
単振動は等速円運動の射影である。

単振動というと、ばねの先に重りをぶら下げて…
という風に、すぐに考えてしまいますが、実はニュートンの発想は、違っていました。

ニュートンは、運動方程式を作り上げて等加速度運動の式を作り上げ、さらには、地上界から天上界へと行って円運動を解析していったわけです。
その中で、とても重要なことを見つけました。

地上界だろうが天上界だろうが関係がない!
円運動の講義の時に、りんごが落ちるように月も落ちているんだという話をしました。それで、その次に彼は単振動の研究を始めたわけです。

この時、すでにフックは、F=kxという力を見つけていました。
ボイルと共に実験する中で見つけたわけですが、これはただの実験式でしかないわけです。なぜこういう風に、Fがxに比例するのかという事を理論的に示したわけでもなんでもありません。ただやってみたら、そうなるというだけです。その時点で、慢心してしまっては本当はいけないんです。

なんでそうなるんだろう。これを考えることも、物理学者の大切な仕事です。
確かに、ボイルの気体の実験から、そのような法則を思いついたわけですから、その発想力たるやものすごいものがあります。だから、それは称賛されるべきですが、しかし、それに満足して研究をやめてしまってはいけません。こんなに綺麗な式が出たのであれば、
なぜそうなるんだろう…?
と、物理学的な観点から検証するべきでした。

なぜこんな綺麗な式が出来上がるんだろう?
と疑問を抱きました。
そこで、まずは、

そもそも単振動って何だろう…??
どんな運動のことなんだろう…??
と考えます。

びょ~んびょ~んびょ~んとなるやつだ!
と、ただ答えて終わりそうですけど…、

ニュートンは、ただの人ではなくて、天才です。
そうは考えないんです。例えば等加速度運動の式が等加速度の直線運動であったのに対して、

円運動っていうのはぐるっと回るということが、まず違うだろう…
ということを考えながら彼は式を作っていきました。ここでもそうなんですが、

一体どういう運動と、どこに類似性があって、何が違うのだろう…??
というようなことを考えようとしたわけです。そして、その時にある一つのアイデアが彼の中で閃くんです。それが何かというと…

今まで彼は、グルグル回るもの、こういうものを研究していたんです。
その時に、こんなことを考えたんです。



なんだそれ?
て感じでしょうけど。光を当てて、ここにスクリーンを置きます。

そうすると物体の影がスクリーンに映ります。やってみましょう。くるくるくるくる回して見て下さい。

影、どうなりますか?
こうなりますよねぇ。
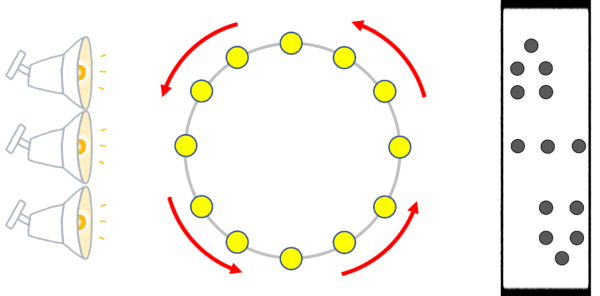
これを円運動の射影と言いますが、

これが単振動じゃないか!?
って、考えたんです。

要は、わかっている運動から単振動に持ってこれないだろうか?
と、考えたわけです。それでは、今からニュートンと同じようにやってみましょう。
単振動の変位、速度、加速度の表記

単振動っていったいどんなものだろう。
その時に、最初は等速円運動の射影なのではないかと考えたわけです。少し絵がややこしくなりますが、とても大切です。

今から作図する絵は、自力で何も見ないで描けるようになって欲しいというくらい大切な絵です。
ただ単に納得するだけで終わらせない方が良いところです。それではやってみます。

まず円を書きます。
数学の単位円と同じように、時刻0で円の右端からスタートすることにして、
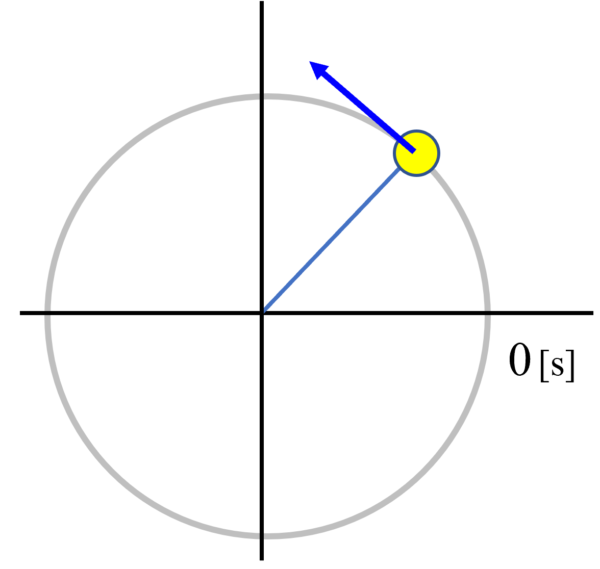
さらに反時計回りにくるくるくるくる回っているものを考えてます。
その時に、左側から光を当てて、
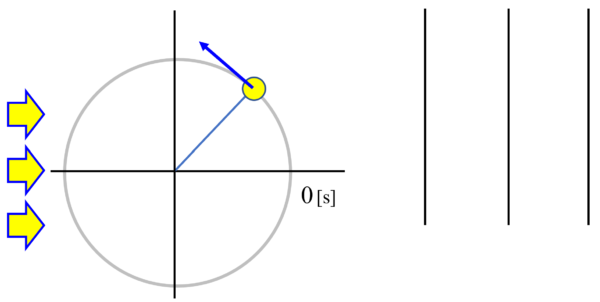

これは自力で描けるようになってください。
右端の黄色い丸が、時刻t=0における物体の位置です。これが反時計回りに円運動していると考えます。
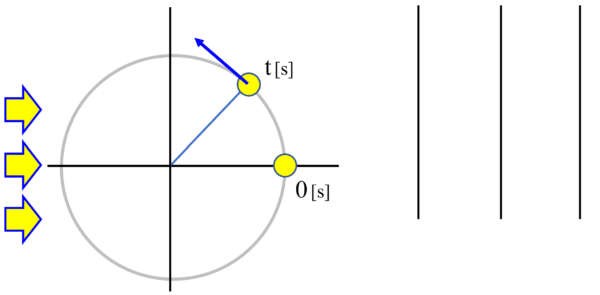
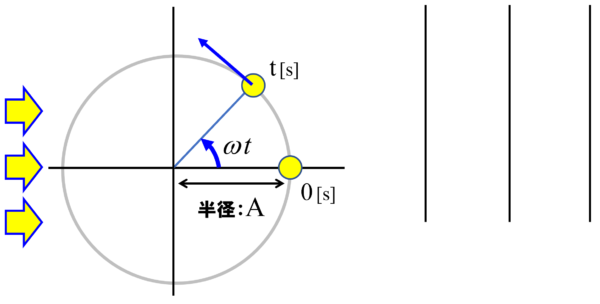

それではいきます。
左側から光が当たっています。

まずは、第1のスクリーンから考えてみます。
時刻t=0においては、影はここにありました。
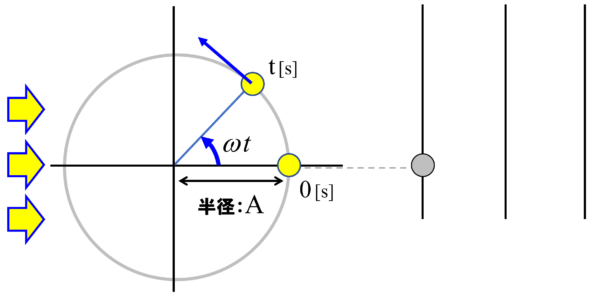
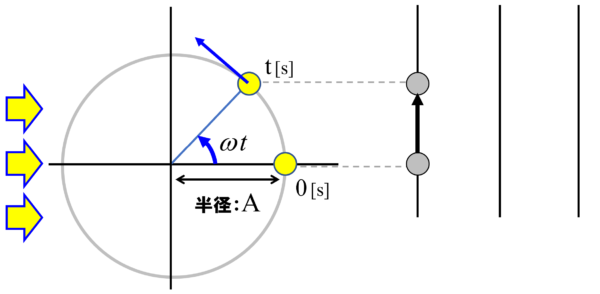

元の位置からずれた、変化したというわけですから、こういうものを変位と呼びます。
この変位をxとします。
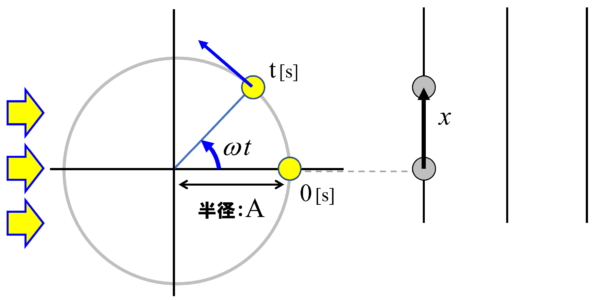
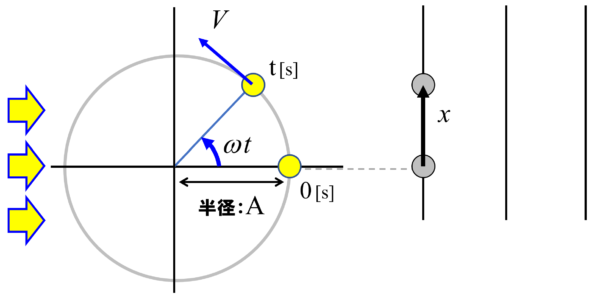

この点が粘土だとして、ここに爪楊枝がブスッとさしてある。この時に横から光があたったとすると、影の長さはどれくらいになるか??
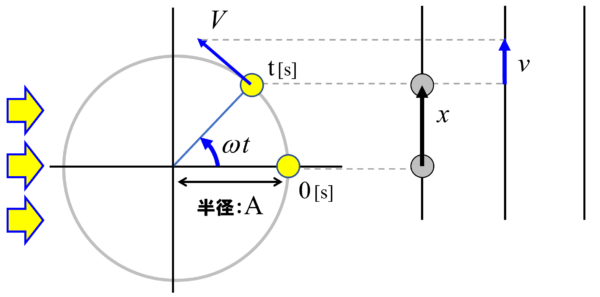
それはこの長さになります。これが影の長さに他なりません。これをvとします。

もしも仮に爪楊枝が1番上に行ったら、影の長さはゼロになります。だから、円の真上では速度が0になります。
こうやって、全部影にしてしまいます。

今度は、変位、速度ときたので、加速度です。
円運動では、加速度は円の中心方向に向かっている。円の中心方向に落ち込むことがわかっている。だから、こうなります。

これをαとします。
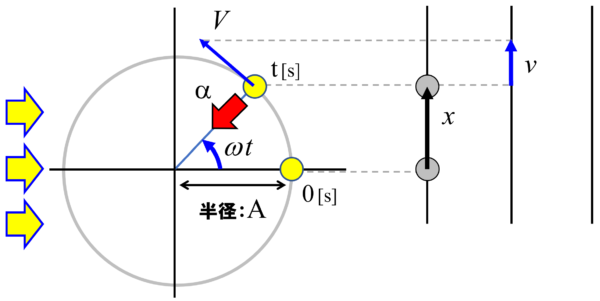
これを3番目のスクリーンに射影してみます。これが加速度aなんです。
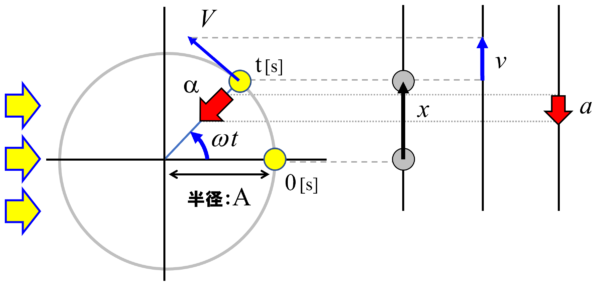

それでは、x、v、a、全て求めていきます。
まずは、xからです。幾何学的に考えていきます。

数学的には、ここで終了しても良いのかもしれませんが、ニュートンが導きたい結論はこれではありません。
xはA sinwt、時間と共にxは、こんな風に変わりますよ!
ということがわかりました。

そうすると、wt側へ爪楊枝を倒した訳ですから、今度はコサインです。
ですから、vはVcoswtとなります。
加速度aは…、

ここからは気をつけてください。
向きが逆になっています。上向きを正としていますから、これはマイナスです。
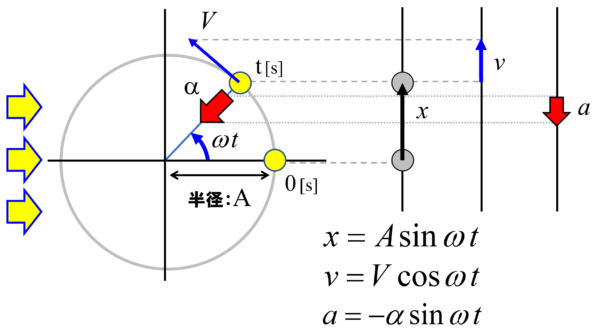

ここで頭に入れて欲しいことは、射影というアイデアを使っていることはもちろんのことですが、ここでは数学的には幾何学しか使っていません。
それで話はまだ終わりではないのですが、続きの話は、次回の記事で行うことします。