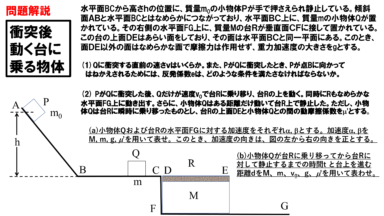
運動の法則と慣性力
以前の講義で運動量と力積にまつわる解法をお伝えしてきた訳ですが、
問題集でこの種の問題を解いていると、解答に少し気になる物理量が記載されていることがあります。


ところが、こうして受験生の皆さんが入試問題を解いていると、突然相対加速度という物理量が当然知っているかの如く登場し、そして初見の高校生を混乱に陥れるわけなんです。

ってことで、慌てて本屋なんかに立ち寄って、難しい物理の参考書を購入するのですが、またこの購入した参考書が何を書いているのかが、さっぱりわからなくて更に混乱してしまうという悪循環にはまってしまう危険性があります。
では、この相対加速度ですが、
全く教科書に触れられていないのか!?
というと、そのようなことはありません。

そういったところの解説を進めて行きます。
慣性力とは
それでは、今回の主題として 運動の法則と慣性力 について進めていきます。
相対加速度について説明する前に、

を理解しておかなければなりません。
慣性力について既に学習済みの方は、この言葉くらいはご存知かと思いますが、

という印象ではなかったでしょうか?

こちらは、比較的容易に理解できたのではないかと思います。
というのが、慣性の法則でありニュートンの運動の第1法則として名を連ねています。ちなみに第2法則が運動の法則。

そして、運動の第3法則が作用・反作用の法則ですね。

こうして、改めてニュートンの運動の3法則を眺めてみるわけですが、

慣性の法則は、言ってみれば物体が止まっているか、等速直線運動しているだけの話で、これは中学時代に既に学んできた内容です。そして、高等学校に入学してから物理を学習すると、第1法則は復習程度に確認して専ら運動方程式や作用・反作用の法則に特段の注意を払ってきたはずです。


そして、その時に、

と、ニュートンの第3法則の存在の偉大さを改めて認識する…、というと言い過ぎかもしれませんが、運動の3法則を見てみると、どうしても第1法則の存在が影を潜めている感が否めません。

それについて、運動の3法則の解釈について今から話を進めて行きます。

皆さんは電車に乗っているところをまず想像してみてください。

朝の通学途中、電車に乗る時につり革に手を掛けたりしますねぇ。
その電車が止まっていたり、一定の速さで運行している時は落ち着いて…、何なら本でも開いて読書なんかも出来るわけですが…、

片手に携帯電話をもって画面を見つめながら、念のためにつり革に手をかけておきますよねぇ。

その電車が目的地に向かって発進すると、


その時に、前方にぶら下がっているつり革を見てみると、斜めに傾いている。


電車が加速しているから、つり革を結ぶひもからの張力の水平成分が引っ張っているだけじゃないですか??


しかし、電車の中でおっとっとって電車と一緒に加速している人から見ると、つり革は静止して見えるんです。それなのに、つり革は斜めに傾いているからつり革にはたらく水平方向の力がつり合っていない。

ちなみに、電車の外から静止して眺める状態のことを慣性系、加速する電車の中で眺める状態を非慣性系という訳ですが、

あらゆる物体の運動をつぶさに表現できると思われていた運動方程式が成立しない。
速度変化する状況下で物体を眺めることは滅多にないことですが、それでも運動方程式が使えないのはもったいない。

この電車の例でいくなら、仮に加速度aで動く電車の中で、質量mのつり革を眺める時には、
という訳です。そうすると、加速する電車の中でつり革を眺める人からすると、つり革を結ぶひもの力の水平成分と慣性力がつり合っている。だから、つり革は静止していると考えることができます。

これが、慣性力の説明になるわけですが、そうすると…

って、言う生徒がいますねぇ。
まぁ確かに、つり革も電車と一緒に加速していることはわかりますが、

要するは無意識のうちに、電車の外で静止して眺める慣性系の立場になっているんです。
最初の内は加速する状態で眺めるという感覚がどうしてもピンとこないので、慣性力が難しく感じてしまいます。そのような場合はこのように考えてください。

トンネルの中にリニアモーターカーが止まっています。

リニアモーターカーは、床の上を磁気力で浮かんでいますから、走行中にレールと車輪がこすれ合う音など聞こえないはずです。だから無音の状態だと考えてください。

その車内でつり革がぶら下がっている。まぁ、実際にはつり革なんてないでしょうけど。あると考えてください。


カメラ映像を見ている時にリニアが加速すると、当然つり革は傾きます。

トンネルの中ですから、外は真っ黒で景色の変化から運動の変化を察知することは出来ないですし、床の上を浮いてるのでレールと車輪の摩擦の音も聞こえないから走っているのか止まっているのかもわからない。もっと言うと、車内の様子を遠く離れたモニターで観察しているから急降下するジェットコースターのように加速する時の圧迫感を感じることもありません。

物理を教える先生の中には、慣性力のことを「お化けの力」と例えて表現ことがありますが、加速するモニター越しに物体を観察するというように、

ここで慣性力にまつわる内容を、まとめておきますと、
・慣性の法則が成り立たない状態で眺める人を非慣性系
といい、
非慣性系においては、運動の法則を成立させるためには慣性力を仮定しなければならない!
慣性力を扱う問題の解説は、次の記事で解説することとして、

運動の第2法則:運動方程式ma=F
運動の第3法則:作用・反作用の法則
今回の慣性力の話は、「非慣性系という観測者の立場では運動方程式や作用・反作用の法則が成立しない!」ということでしたねぇ。

さぁ、そこで最後の締めに入りますが、
講義の前半に、
という疑問を投げかけた訳ですが、今回の話の流れを理解していただければ、慣性の法則が必要な理由がわかっていただけたと思います。

もしも、運動の法則から慣性の法則をとってしまったら大変なことですよねぇ。

としたらまずいですよね。
だからニュートンは、このように宣言する訳なんです。
質量mの物体にはたらく力と加速度の間には、ma=Fという関係が成立して、接触する物体間にはたらく力には、作用・反作用の法則が成り立ちますよ。

と…

その上で、運動方程式と作用・反作用の法則が成り立つ…

これで慣性力にまつわる話は終わりますが、慣性力というと多くの受験生が苦手にする内容です。特に難関大学への進学を考えている人ですと、慣性力を解法として運用できるかどうかで差がつくところになってきますので、この講義を参考にぜひとも理解を深めていってください。