はじめに

 

運動量の内容について、問題解法にまつわる知識から実際の問題の確認までを行っていきます。

ここでは、問題解法に必要な運動量の基本法則について解説します。

このページでは運動量と力積について学習します。その他の項目については、下記を参照してください。

主題１．運動量の基礎

この項目では、大学入試問題を解く上での前提となる知識の確認を行っていきます。

要点資料は、以下より閲覧およびダウンロードできます。

 

今回は運動量についてお話をします。

 

と言いわれると、学習済みの方からすると、

 

確かにその通りですが

 

　運動量って何？　

と聞かれた時に、mvと答える受験生が多いわけです。

 

そう聞き直すと

 

って聞くと…

そんな感じで会話が無限ループしてしまうわけです。

 

簡単に言いましょう。

という風な捉え方がちゃんとできるかどうかが大切です。

 

そう言われると、

 

 

　1/2mv²  運動エネルギー

　mv 運動量

どちらも運動の激しさを表していると言っても問題はなさそうです。

 

 

そういったところを理解していかないといけません。

１．運動量と力積

ここでは、運動量と力積の関係について学習します。

 

まずここに質量ｍの物体を置いてみます。

 

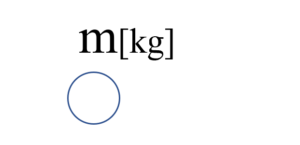
滑らかな床の上と考えてもらえれば結構です。そこに、後ろから僕が手で、ぎゅっと押したと考えてみましょう。

 

 

この物体を力Fでぐっと押したとします。力とは運動形態を変化させるもので、質量ｍの物体に力Fが加わったわけですから、当然この物体は右向きに動き始めます。

 

 

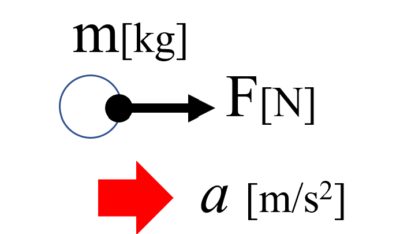
止まっていたものがどんどん速度を上げていきます。

 

 

これは完全に物理基礎の復習になります。そうしますと、ニュートンの運動方程式が成立します。

 

なんて書いたらダメですよ。物理学には必ず意味がありますからね。

 

物理とは、物の理（ことわり）と書くわけですから、そこにはかならず理由があります。

 

こういう意味ですね。それが運動方程式 ma = F。すなわち、力Fがどちらかというと結果なんです。

 

こういうのを因果関係と呼んでいますね。

 

ですから、「maとFというのが互いに釣り合っている！」という意味とは違います。

 

と、和訳できることが大切になってきます。

 

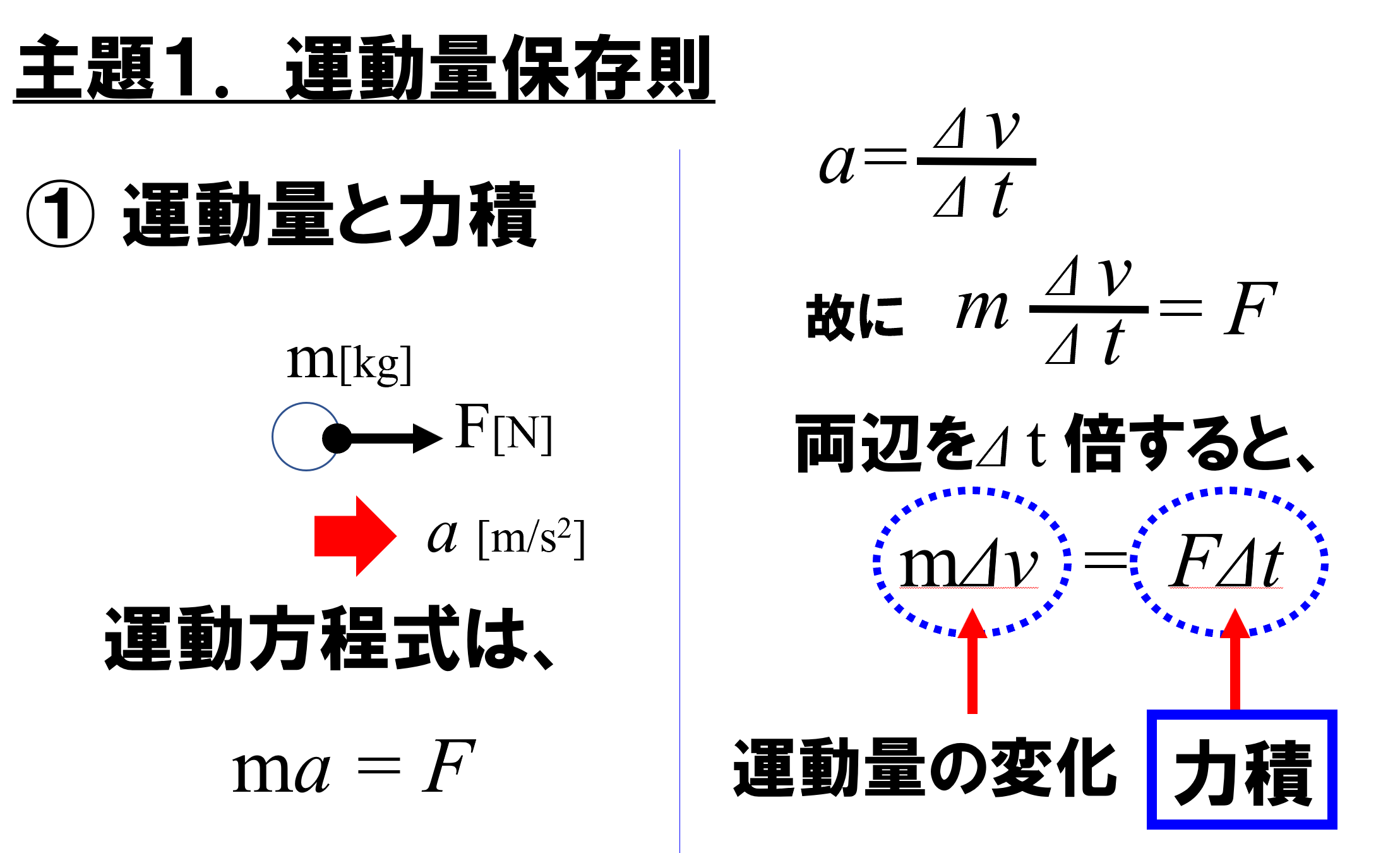
 しかし、これでは運動量と力積の関係にはなっていません。皆さんご存知の通り、運動量はmv で定義をされています。じゃあ、これ（ma = F）ではまずいですね。しかし、加速度というのは、もう一つ定義を持っていました。それは、

 

 

これが加速度の定義です。それでは、ここで式を書いてみましょう。加速度は、どう書けるか…

 

 

a = Δv/Δt と書くことができます。ですから、これを代入してみましょう。質量ｍの物体に加速度aを生じさせたのは、力Fですよ。

 

 

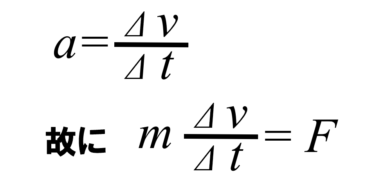
mv を作りたいのですよね。

 

そうしますと、ここにFが出てきて、ここにΔｔが出てきます。

 

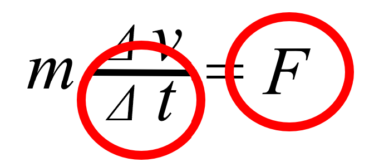
そこで、両辺をΔt倍してみると、mΔv＝FΔt　となります。

 

 

ちょっと運動方程式を変形させただけですが、とても重要です。

 

運動量と力積について

さぁ、それでは、mΔv＝FΔt　という式が出てきましたが、

因果関係を表す、ma＝Fでしたね。それをちょっと変えただけですよね。

 

そうすると、ここを見てください。

 

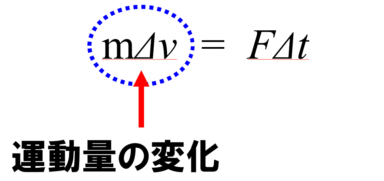
これ（mΔv）は運動量の変化量を表しています。

 

一つの物体に力加えただけですから。ここの部分（mΔv）というのは、運動量の変化を表しているわけです。

 

という訳です。もともと物体は止まっていました。そこに力が加わったからv という速さになったわけです。

 

 

こいつ（FΔt）ですか。これ（FΔt）はなんでしょう？

 

力に時間がかけてある…

 

 

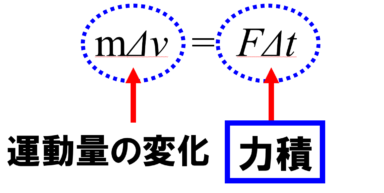
これは覚えないといけない用語なんですが、これだと単に

 

　運動量の変化は力積に等しい

 

になってしまうんですね。

 

 

それは物理じゃないです。意味がわからないといけないです。

 

 

もう一度行きます。止まっていたんです。そこに力が加わると、速さｖになったわけです。誰のせいですか。ここ（FΔt）に原因があるわけです。

 

　力Fですよ！

 

とは、書いてないですね。力FにΔtが掛けてあります。

 

少し戻ります。ここです。

 

 

 

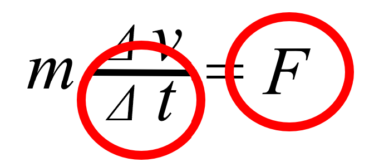
分子にある速度が変化しているから、速度が変化している時間ですよ。

 

ということは、ある力FがΔt秒間、働いたために、こんな風（こんな数式）になっちゃったってことです。力が働いたから、こうなったんじゃないですよ。

 

運動方程式に戻ります。

 

こちらはそれでいいんです。しかし、こちらはそうはいきません。

 

 

 こちらは力だけではないです。どう解釈すればいいのか。

 

力の距離的効果と力の時間的効果

 

 

そこでですね、参考として、

 

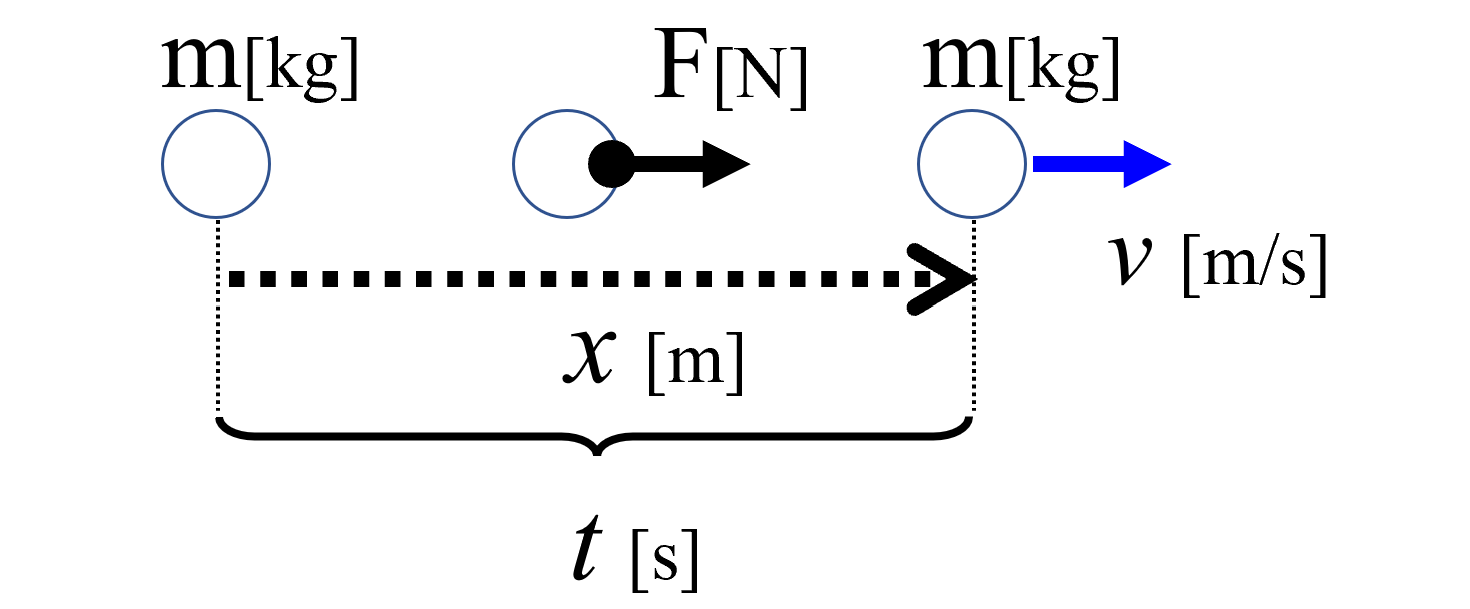
質量ｍの物体が止まっています。ここに力を加えました。力を加えることによって、この辺り（距離x[m]）まで移動した時に速度ｖに変化した。

 

 

同じ物体です。力Fを加えて「すーっっと」。左側から右側まで行く時に、ずーっと力Fが加わっているわけです。

 

 

左側から右側までの距離をxと置きます。

 

最初物体は止まっていました。それが距離xだけ動いて速度がｖになった。これだけの距離に力Fを、が～っと加えたわけです。

 

 

 

物理基礎の範囲です。物体に仕事をしたせいで、こいつ（左側の物体）がこんな（右側の物体）になっちゃったんです。

 

 

最終的には1/2ｍｖ²になったんですね。運動エネルギーは物理基礎で学んだものでした。一番最初は、1/2ｍ•０²ですよね。止まってましたから。

 

 

ということで、

 

それでは、こっからここまでの所要時間をｔとすると、どんな関係があるか。こんな関係になるんです。

 

 

わかってもらえたかなー。

 

 

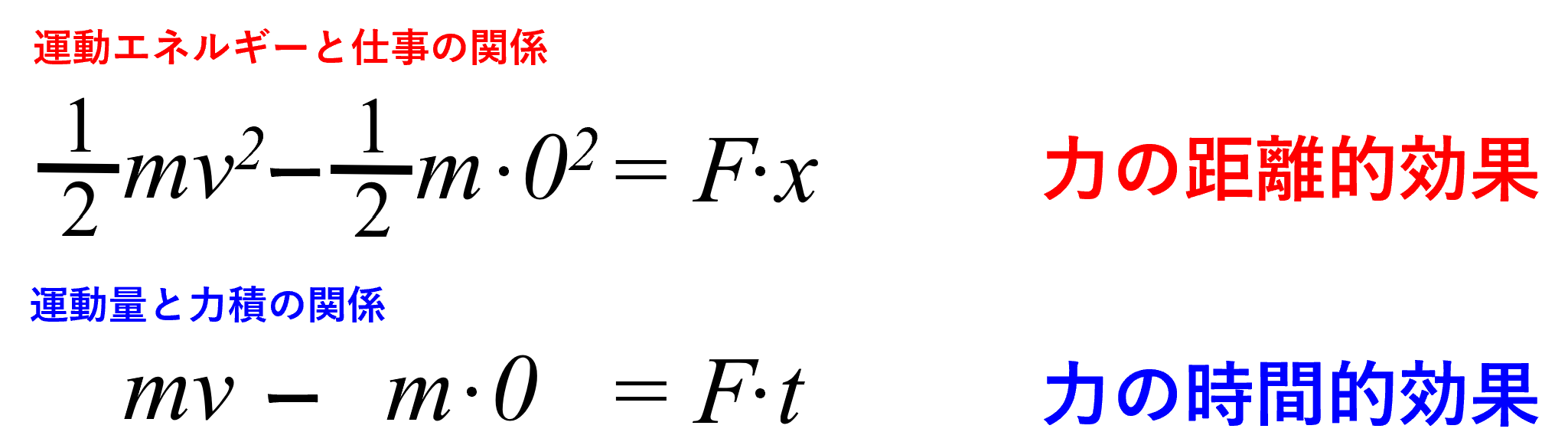
（運動量と力積の関係）が力の時間的効果ですから、（運動エネルギーと仕事の関係）は、力の距離的効果です。

 

私は、中学生の頃は卓球部だったのですが、飛んできたピンポン球をラケットで打ち返す時に、ラケットをこう傾けて、カンカンカンと、ピンポン球を打ち返すんです。

 

そうすると、速く鋭い球を相手のテーブルにはじき返すことが出来るんです。この時に、ラケットを傾けないで、打ち返そうとすると、ピンポン球がテーブルを飛び越えてしまいます。

 

少し練習したらすぐ出来るようになるんですが、球の返し方がわからないと、鋭い球を打ち返すことが出来ないんです。

 

だから、素人だと、温泉卓球みたいに、ピンポン球をすくい上げるようにぽよよ～んとした玉しか返せないわけですね。

 

それでですね。私が友人とテニスをやると、卓球部の時の感覚でついやってしまうものですから、ラケットをかぶせながら飛んできたボールを返そうとするわけですね。

 

そうするとね、ネットすら通り超えられず、ボールが「ぽとんっ！」と地面に落ちてしまうわけですね。

 

 

それで、テニスが上手な友だちの真似をしてみるわけですが、友人のスイングを見ていると、こうラケットの面を下に構えた状態でボールをとらえながら、手首のスナップをきかせながら、ボールとラケットの接触時間を稼いでいるんですねぇ。

 

 

何が言いたいかわかりますか？？

 

 

私は、大学時代にアメリカンフットボール部に所属していたから、一般の人よりは力に自信があるわけですが、力任せにフルスイングしてもボールは、遠くに飛ばないわけです。

 

ボールと接触したときに、ラケットとボールを接触させて力を加える時間を稼ぐ、もしくは、力を加える距離を稼ぐことで、鋭いボールが打てるわけですねぇ。鋭いボールとはつまり、運動の激しさのことですね。運動量、運動エネルギー。そして、力の時間的効果と力の距離的効果です。