
2.運動量保存側
ここでは、運動量保存側の成りたちについて確認します。

運動量と力積の関係がわかってもらえれば、どうってことないですね。
今から例を挙げてを考えてみたいと思います。
衝突という現象を考えてみましょう。



■衝突の状況設定

それがv0という速度であるとします。
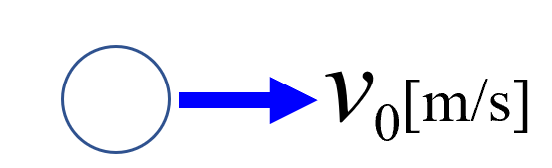

止まっているとでもしときましょうか。
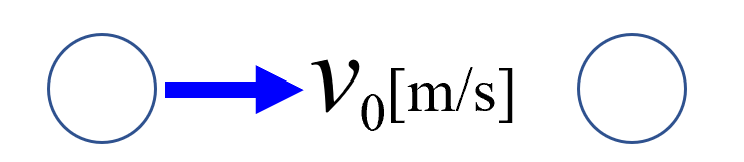

こちらをmAで、こちらをmBと…
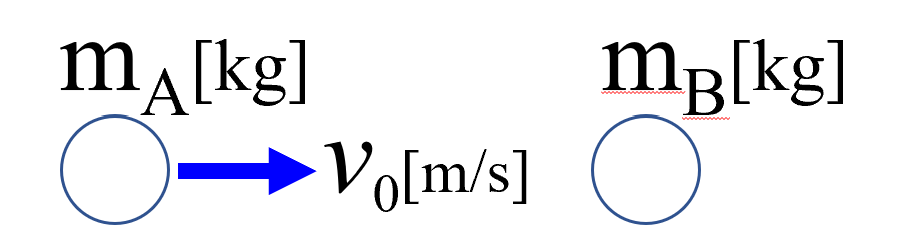

その後、どうなったか…
mAの物体はvAになったよと。mBの物体はvBという速度で動き出したよと…。
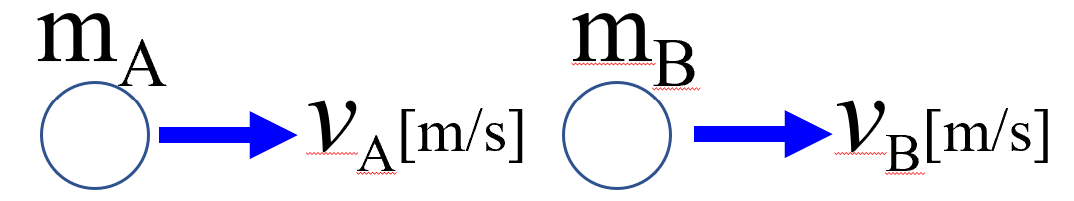

さぁ、やってみましょうか。
これ(左)が、衝突直前ですねぇ。これ(右)が衝突直後という風に考えた訳ですねぇ。
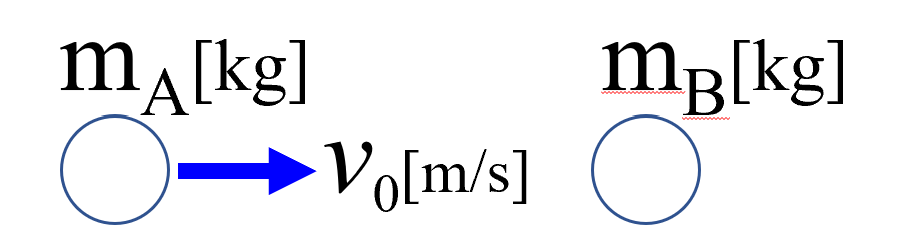
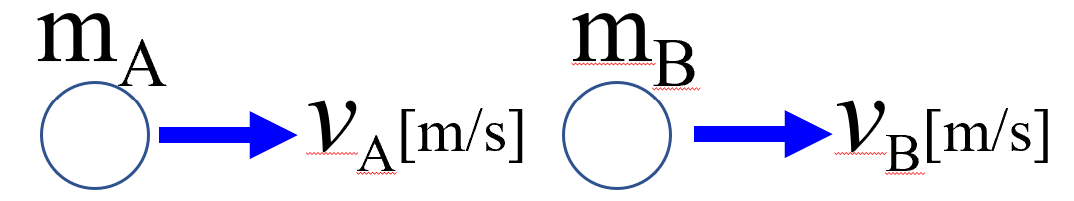

これは止まってたんでしょ。
それで衝突したら動き出します。
ということは、何か力が働いたんですよ!

(衝突後は)v0じゃないですよねぇ。
ということは、何か力が働いたんですね。
それならば、その力をちゃんと明確にしなければなりません。

という訳です。

ぶつかった瞬間をここに出します。
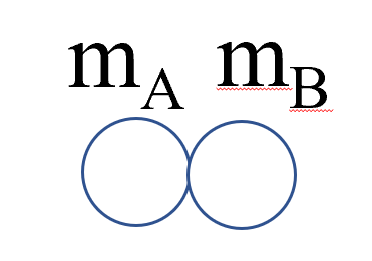

学生さんは運動量保存則を考える時に、衝突前の画があって、衝突後の画があって、

って、よく口にします。
確かにそうです。結論は。

だから、その原因となった力を探らないといけなんです。じゃあ、ぶつかった時に力は互いに働いたはずです。

ところが、力を書く時に気をつけないといけないのが、ぶつかった瞬間にはたらく力は接触力ですから、作用反作用の法則ですねぇ~。
Bには、こんな力が働いたでしょうが・・・、
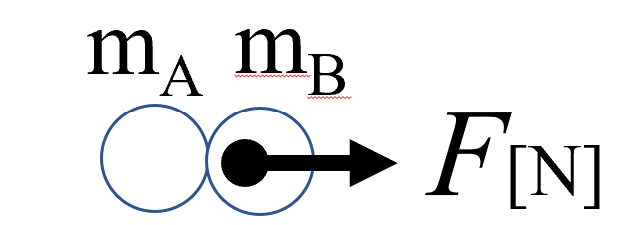
Aには同じ大きさで反対向きに、こんな力が働いたはずです。
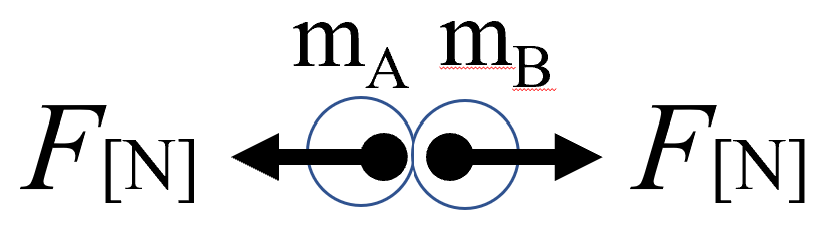
力が働いている以上、速度が変わっているのを見たらわかると思いますが、加速度があるはずです。
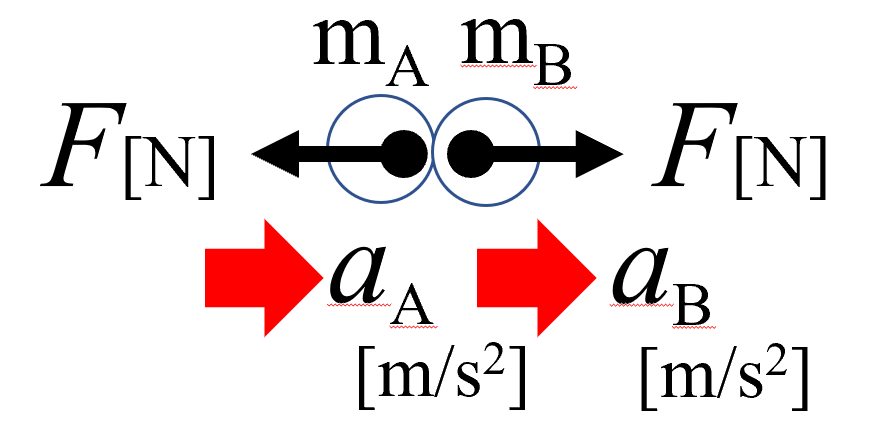
全部右向きを正としましょう。

減速するでしょうからね。
■運動方程式の立式
さぁ、それでは続けて行きましょう。
ここ(青い部分)で運動方程式が立てられますね。
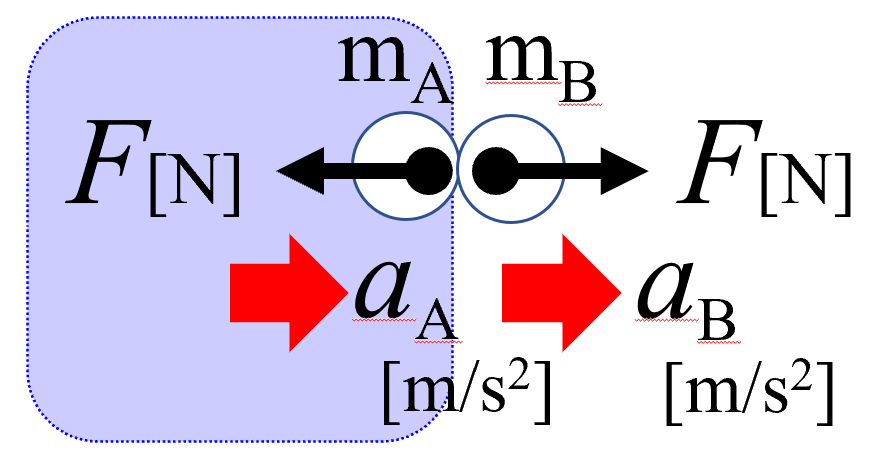
ここ(赤い部分)で運動方程式が立てられますね。
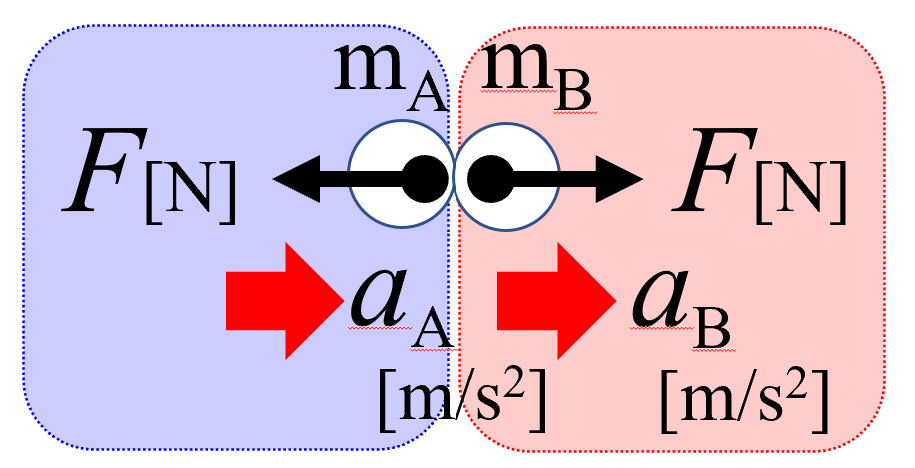
では、立ててみましょう。
運動方程式は、
ですねぇ。
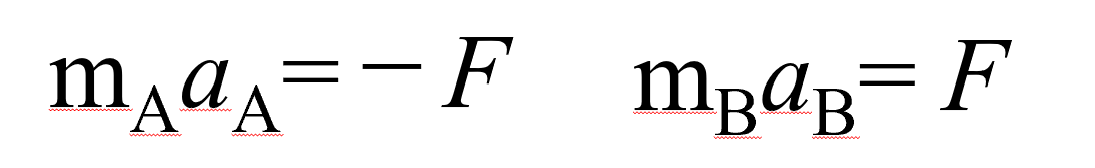
難しくないですよ。これで良いでしょう。

運動量の関係が欲しいんですよ。
それは、前回、力積のところでやりましたね。
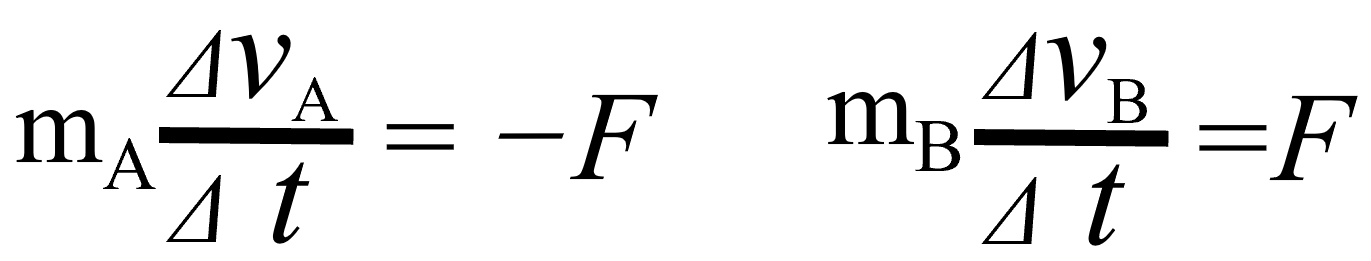
どうですか。

それでは、皆さんに質問です。
別に当てるわけじゃありませんからね。
でも、ちゃんと考えてくださいよ。
何でこれ、Δtに添え字が無いんですか?? これ(赤い〇の部分)。
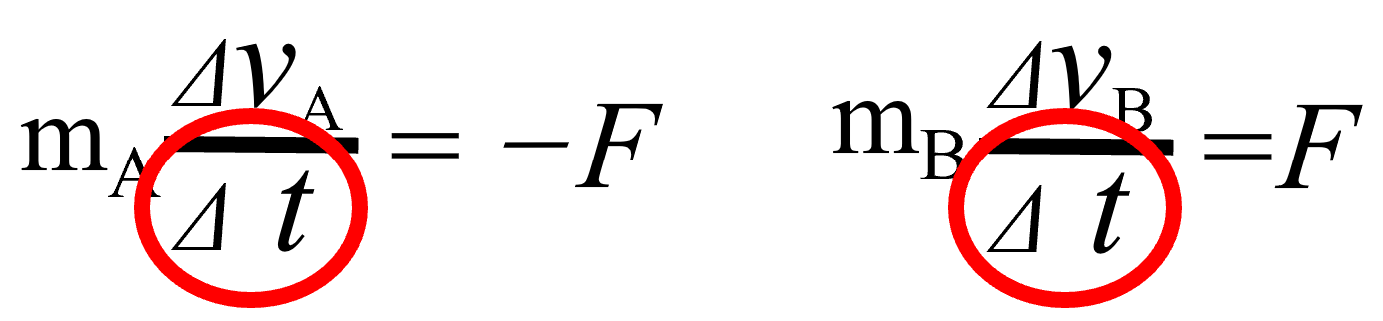
ΔtA、ΔtBじゃないんですか。何でΔtなんですか。これ。
今みたいなところを誤魔化されてはいけません。
本来であれば、ここにAとかBとか入るはず。でも入れてないんです。






力が働いた時間ってことは、接触時間ですねぇ。


でもね、理由を考えるのと考えないのとでは、大違いなんですよ。
こうやって、何がわかるかというと、力は互いに逆向きだけど、同じ大きさなんです。時間Δtも同じなんです。だから、同じもの集めてみる。


前回やりましたね。今回もやってみましょう。
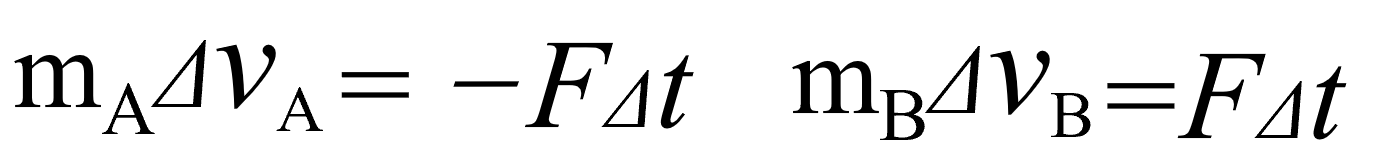
こうですね。
じゃあ、行きます。ここ(青の枠内)をよ~く見て下さい。
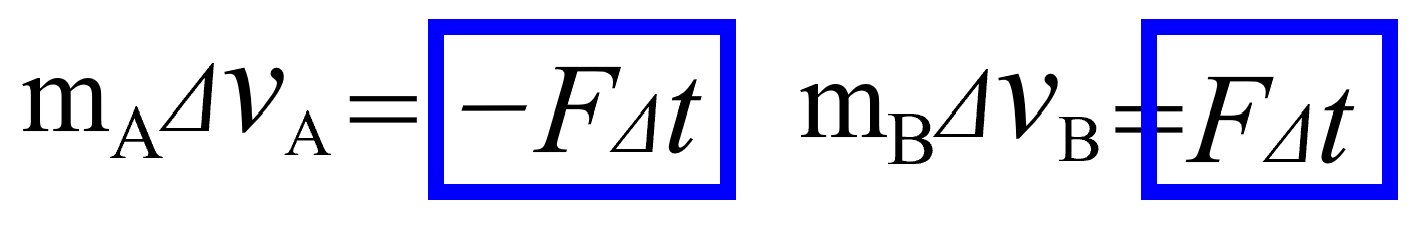
(Aに関する式の右辺は)どのぐらいの力積が働いたか、(Bに関する式の右辺は)どのぐらいの力積が働いたか、

ということが書いてある。
FΔt、FΔt。大きさが同じです。だけれど逆向きなんです。

それじゃ、今、青色の線で囲んだところを足すと、これはゼロですねぇ。ということは、まず左辺同士を足すと、mAΔvA+mBΔvB
右辺同士を足すと…、ゼロ。
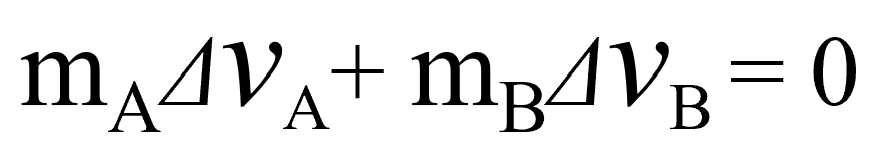
いいですねぇ。和訳してみましょうか。
だから、どういう意味ですか?

■運動量保存
いいですかぁ。こういう時に、

って思っちゃだめですよ。
私は、小学生にもわかること言ってるんです。
ちょっとやってみましょう。今の流れを逆から辿っていきます。
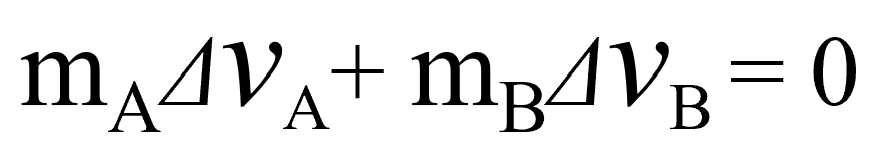
これが成り立つためには、次の2式が成り立たないといけないんです。
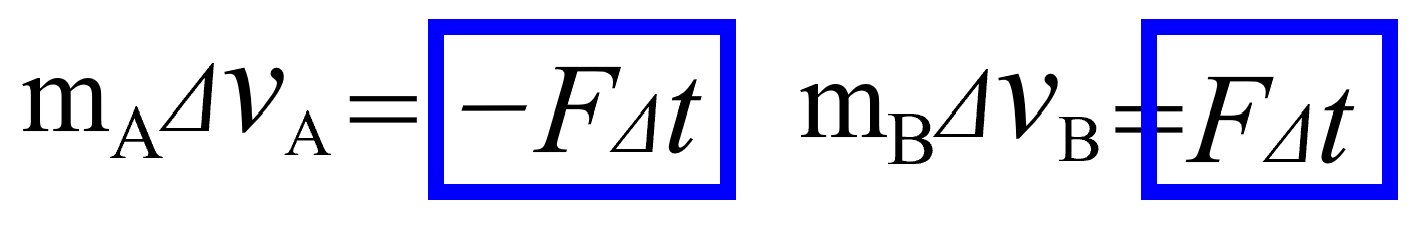
互いに逆向きで同じ大きさでなければダメなんですよ。
しかし、接触時間が同じですから~、(両辺をΔtで割ると)
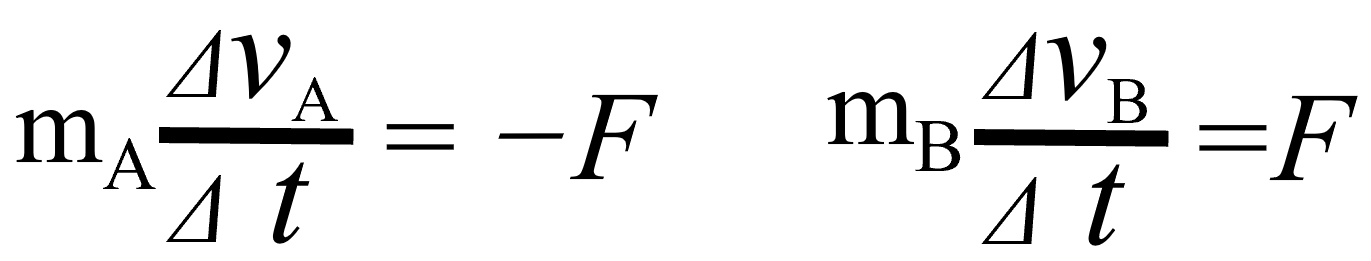
左側の式がーFで右側の式が+Fでなければいけないんでしょ?
これを足し算したいんでしょ。ーFとFを足したら、ゼロでしょう。
ということはね、最初の図へ行きましょう。
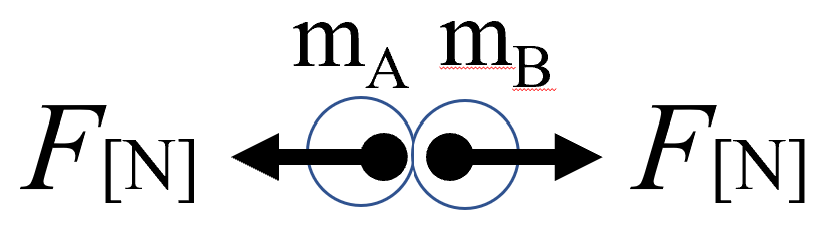
こうやって書いてあるけども、


要するにね、mAとmBの間でやりとりがあったかもしれないけれどもね、何かね、外から私がガーンっとか、やったとか、そういうのではないんです。
勝手に、2つの物体AとBがやり合っただけです。

外から何も力が働いていない。


それは小学生にでもわかりますよ。
だから、
1個1個の物体を見たならば、片方に力F、片方にーFということですが、全体としてみたら力が働いていないという意味です。
「外から力が働いていないんだから、運動の激しさは当然変わらない。」
という事になる。

少しだけ、式を進めてみましょうか?
まぁ、進めるって言ったって、大したことではありません。

ですから、

って言われたら、



それがイコールゼロと。
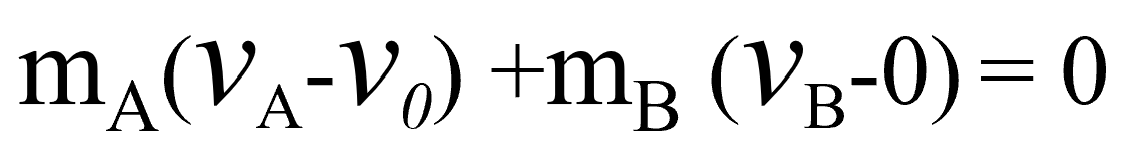
これで大丈夫ですね。
そうすると、-mAv0とーmB・0を右辺に移項しましょう。
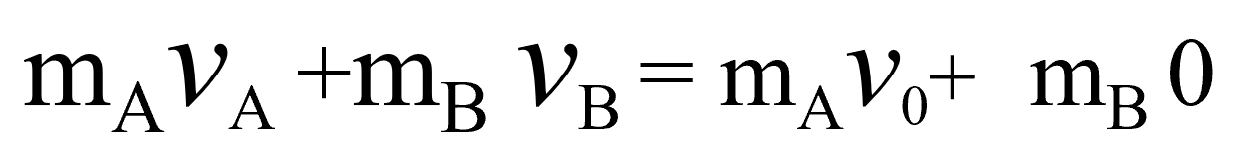
これでいいでしょう。
この式の右辺が、物体AとBが一番最初に持っていた全運動量です。
そして左辺が、衝突後に持っている全運動量ですね。
ちゃんとなってますね。

以上のことをまとめると。
何もいかにも難しいことをやっているようですが、用語が難しいだけですね。小学生にもわかりますねぇ。
って書いてあります。

って言われたらおしまいですね。ここなんですよねぇ~。

当たり前のことしかやってないんです。
でもそれをねぇ、

って言ったら物理は始まらない。

物理ってどこから学問として始まったか。
りんごが落ちるところから始まったんですよ。それで、りんごが落ちました。

って言ったら物理学は始まっていないんですね。
だから、

そこには理由があるんです。
地球との万有引力によって、引っ張られたんだ!
だから下へ向かって落ちていったんだ!
っていう理由があるわけです。ところが、一般の人たちは、それを当たり前じゃないかって済ませる。しかし、ニュートンは、当たり前…としなかったんです。


ですから、運動量が保存するの、当たり前じゃん。衝突じゃないか。そうやって済ませてはいけない。どうしてっていわれた時に、ちゃんと答えられないといけない。
そんな考え方をちゃんと持たなければいけないということになるわけです。
こうやって理屈っぽいことを言うから、一般の人には

とか、そういう風に言われるのかもしれないですけど、私に言わせると、物理は、ここに書いてあるように、とっても簡単なことをやっているんです。普通の人が聞くと、当たり前じゃないかというようなことをやっているんです。
しかし、それを第三者にもわかってもらえる数式というものを使ってやるために、難しく見えてるだけです。
だから、

と思っている人、

と思っている人、

ということですね。

というところの境目
と言っても過言じゃないと思います。
さぁ、これで大体、運動量保存則の話は終わりました。















