はじめに
今回は三角比について確認します。
□動画による解説はこちら↓↓↓
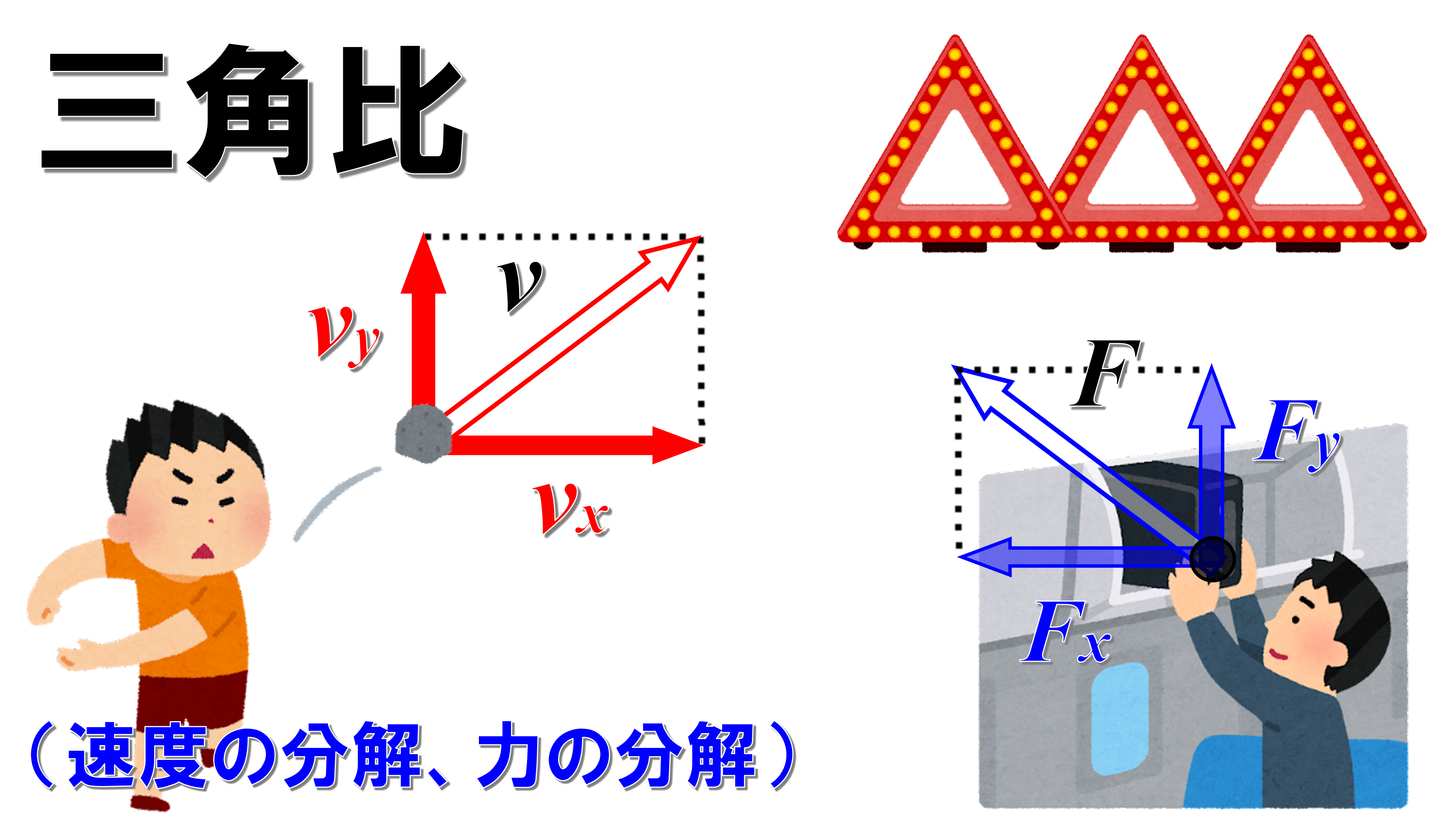
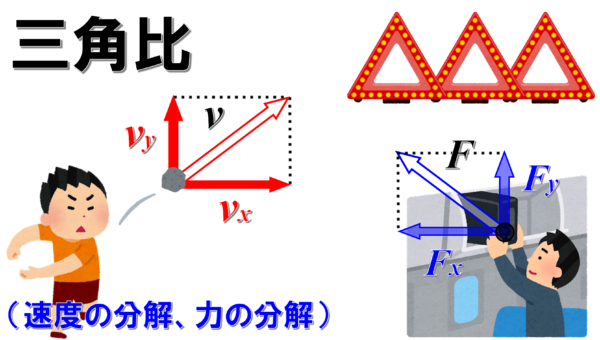
三角比は高校数学で学習する項目ですが、物理においては平面の運動における速度の分解や力の分解において必要になってくる内容です。
三角比を使うと、平面上を移動する物体の速度の水平成分や鉛直成分であったり、物体にはたらく力のうち、物体の進行方向の成分をスムーズに算出できます。
それ故、頻繁に使用する三角比ではありますが、高等学校によっては、この三角比を数学で習う前に、物理の学習で使用するために混乱を招きやすいところです。
そこで、ここでは物理の学習に最低限必要な三角比の計算方法を確認していきます。
三角比について

三角比とは、直角三角形の辺同士の比のことです。
直角三角形では、もう一つの鋭角の大きさが決まるとすべての角の大きさが決まり、辺の比も決まります。
このことを利用し、角度と辺の比を対応させたのが三角比です。
(どんな三角形でも、3つの角の大きさの和は180°、相似な三角形では対応する辺の比は等しい。)
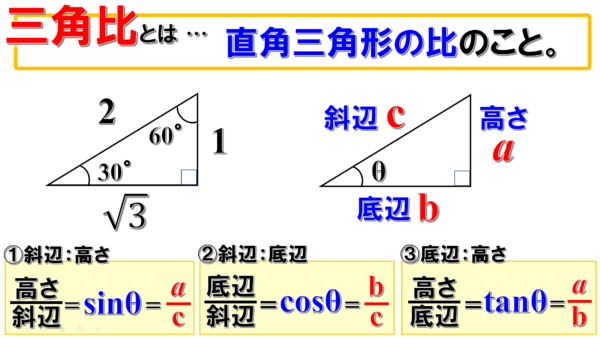
この時、図の斜辺と底辺の為す角度がθの直角三角形において、
高さ 対 斜辺 の比の値を sinθ(サインシータ)
底辺 対 斜辺 の比の値を cosθ(コサインシータ)
底辺 対 高さ の比の値を tanθ(タンジェントシータ)
と定義します。
したがって、直角三角形の各辺の長さをa, b, cとすると、
sinθ=斜辺分の高さ、 つまり c分のa
cosθ=斜辺分の底辺、 つまり c分のb
tanθ=底辺分の高さ、 つまり b分のa
となります。

このように定義された三角比は、一覧表(教科書の後ろの方に掲載されている)に整理されており、どのような角度であっても速度や力の水平成分や鉛直成分が算出できるようになっています。
三角比を用いた計算
鉛直成分の求め方
例えば、水平面と30°の角度を成して、初速度10m/sで物体を打ち上げたとします。この時の初速度の鉛直成分の大きさvyを求めてみます。
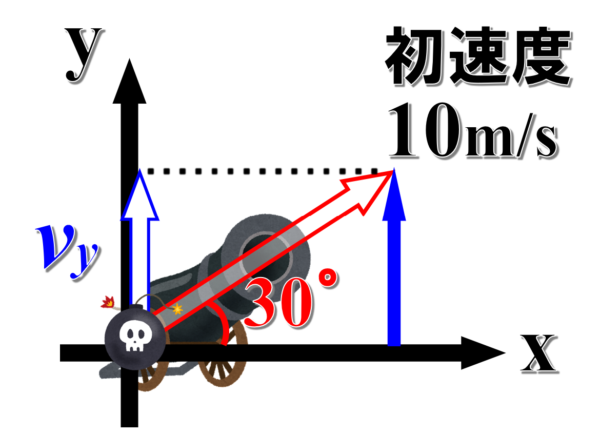
打ち出した方向は、直角三角形の斜辺、鉛直成分は高さに相当するので、

斜辺と高さ… 斜辺 対 高さということで、sin30°の値を調べます。
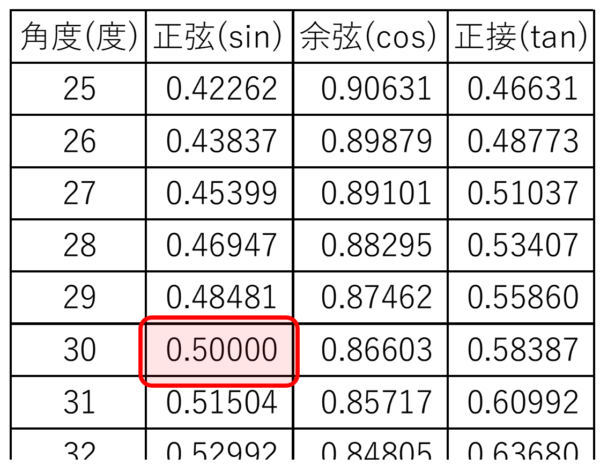
三角比の一覧表によるとsin30°は0.5です。
一方、三角比の定義よりsin30°は、斜辺分の高さでも表現できるので、10分のvyと書けます。この2つの値は等しいので、この式からvyを求めると、

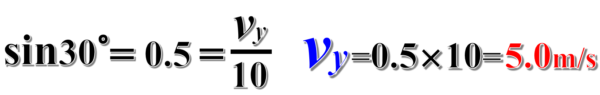
vy=10sin30°
つまり5m/sであることがわかります。
水平成分の求め方
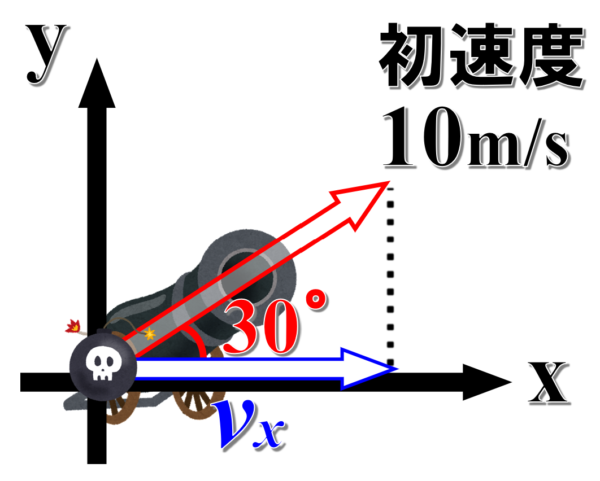
次に水平成分の大きさvxを求めてみます。

水平成分は直角三角形の底辺に相当するので、今度は斜辺と底辺、斜辺対底辺ということでcos30°の値を調べます。
三角比の一覧表によるとcos30°は0.86603です。
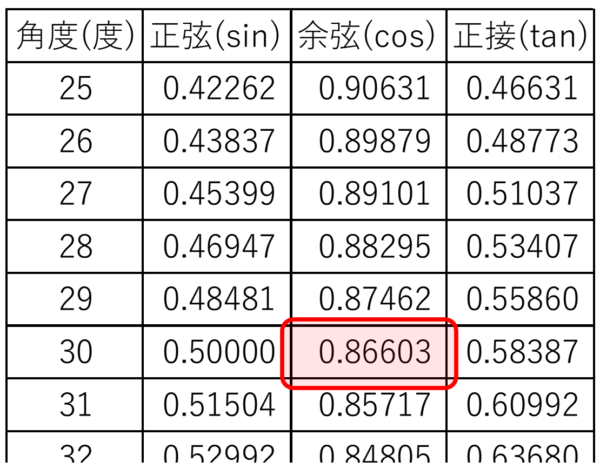
一方、三角比の定義より、cos30°は、斜辺分の底辺でも表現できるので、10分のvxと書けます。

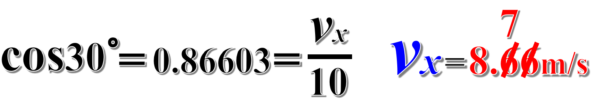
この2つの値は等しいので、この式からvxを求めると、vx=10cos30°、つまり8.7m/sであることがわかります。
水平成分と鉛直成分の分解について
ここまでの内容をまとめておくと、
水平面から角度θをなす物体の速度を、水平成分と鉛直成分に分ける場合、
水平成分であれば、cosθ
鉛直成分であれば、sinθ
をそれぞれかけると覚えておくと、
スムーズに縦方向、横方向に物体の速度を分解することが可能です。
力の場合も同様に、水平面となす角度θに対して
水平成分であれば、cosθ
鉛直成分であれば、sinθ
をそれぞれかけると、それぞれの方向成分の力が求められます。
代表的な三角比
これまでに三角比を用いて、速度や力を分解する方法について確認しましたが、代表的な角度を持つ直角三角形の三角比については、自分自身で求められるようになっておく必要があります。
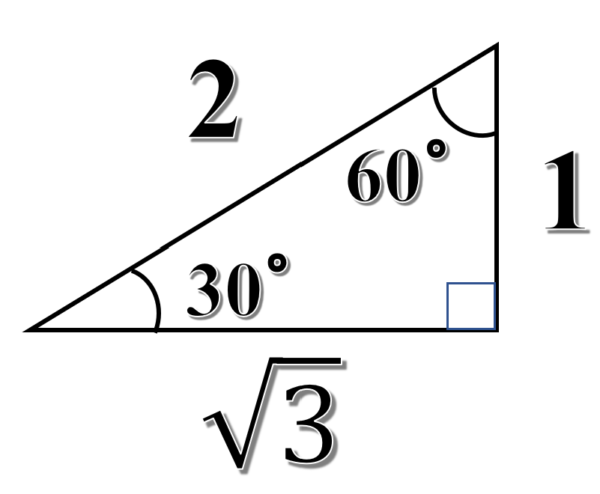
代表的な角度とは、水平面とのなす角度が、30°、45°、60°の直角三角形です。
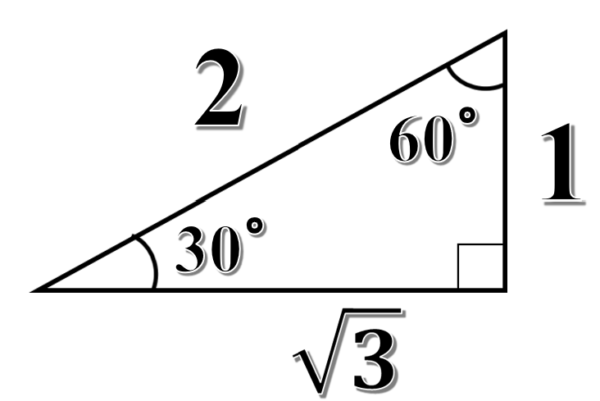
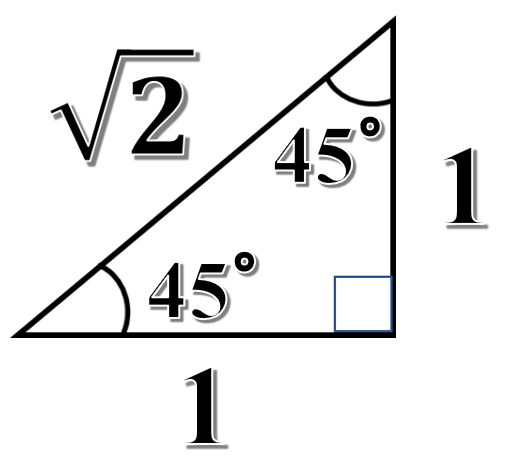
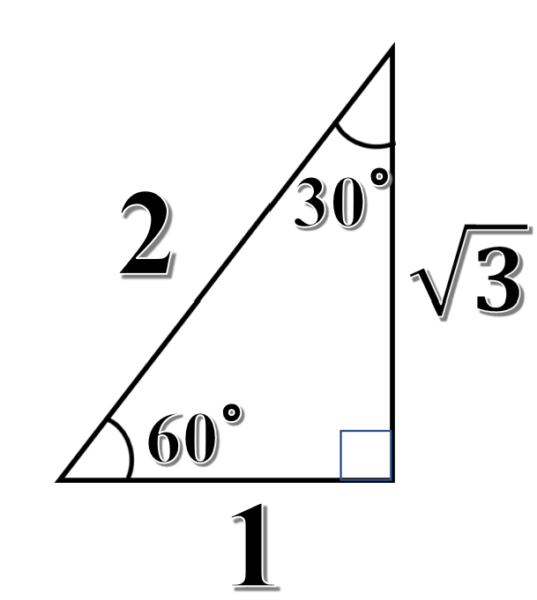
これらの三角形の辺の比は、図のようになっているので、それぞれの角度について、表にまとめていくと次のようになります。
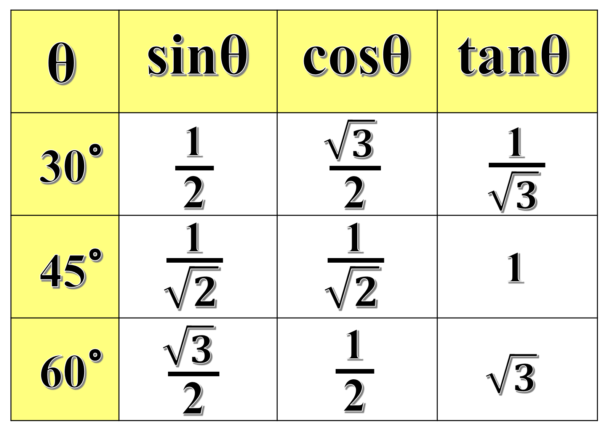
これらの値は覚えるのではなく、直角三角形の辺の比より自分自身の手で導出できるようになっておくことが必要です。
これで三角比の説明は以上となります。














