目次
はじめに
今回は小中校生を対象に、割合について解説します。

割合は小学5年生の算数で学習する内容で、中学生や高校生にとっては学習済み項目です。
だから、多くの中高生に

割合って何?
って聞くと、

それって、全体割る部分のことでしょ!
って応えてくれるわけですが、

何で全体を部分で割るの?
とか

何でそんな計算するの?
って聞くと、途端に答えてくれなくなったりします。
中学校や高校で理科授業を行っていると、

濃度計算が苦手だ!
という生徒を度々見かけます。

しかし、その原因を探ってみると、実際は濃度計算が分からないのではなくて、
「割合についての理解が浅いこと」が、根本的な要因であることがしばしばあります。
そこで、今回は「割合」の計算が必要になってくる具体的な例を確認しながら、
「割合とは何か?」という、「割合」の定義について見ていきます。
それでは、早速始めていきます。
□動画による解説はこちら↓↓↓
バスケットボールの試合にて
まずは、次のような状況を考えてみます。
バスケットボールの試合を3試合行いました。

それぞれの試合で、まことさんとあきさんがシュートをした回数とシュートが入った回数を記録しました。
その結果が次の表のようになったとします。

これについて、今から3つの問いについて考えていきます。
問1:シュートをたくさん決めたのはどちらですか?
シュートをたくさん決めたのは、表の入った数を比べればいいので、あきさんの方が3試合を通してたくさんシュート決めていることがわかります。
それでは、次の問について考えてみます。
問2:シュートが上手なのは、どちらだと思いますか?

この問いについては、どのように答えたらいいでしょうか??
シュートをたくさん決めたのは、あきさんです。

だから、「シュートをたくさん決めた方がシュートが上手い!」と判断するのであれば、あきさんの方がシュートが上手いと言えます。
ところが、シュート数を見てみると、
まことさんは、1試合目が7回、2試合目が6本、3試合目が7本。
あきさんは、1試合目が8本、2試合目が10本、3試合目が12本…
ということで、
あきさんの方がシュートを打つ回数が多かったことがわかります。
したがって、どちらのシュートが上手いかと言われると、

まことさんの方がシュート数が少ない割には、たくさんシュートを入れていた。だから、まことさんの方がシュートが上手い!
という考え方も出来ます。
だから、今のままでは、どちらがシュートが上手いと判断することが出来ません。
「シュートをたくさん打ったのはどっち?」とか「シュートがたくさん入ったのはどっち?」という問いについては、シュートした本数やシュートが入った本数の大小関係を比較したらいいのですが、
どちらが上手いか?
といった優劣の関係は、数値の大小関係だけでは判断できません。
そこで、どちらがシュートが上手いかを検証するために、次のような問いについて考えてみます。
それが問いの3番です。
問3:シュート数が同じなら、「まことさん」 と 「あきさん」では、どちらの方がたくさんシュートを決められると思いますか?
この問いでは、
もしも同じシュート回数だったら、どちらの方がたくさんシュートを決められるか!?
という問題になっています。

こちらの大小関係であれば、「まことさんとあきさんのどちらがシュートが上手いか?」という問いに対して、一定の答えが出せそうです。
とは言っても、3試合を通して、2人のシュート回数は違っているので、今のままでは解答できません。
もう1度試合をするとしても、両者が全く同じシュート回数になるとも限りません。
そこで、この問いに対して解答するために、次のような計算を試みます。
比べる基準を揃える方法
まず初めに、シュートした回数を「1」に揃えてしまいます。
「1」に揃えるとはどういうことかというと、
「シュート数」をそれと「同じ数」で「割る」 。そして、「入った数」を「シュート数」で「割る」ということです。

それでは実際に計算してみます。
まずは「シュート数」を「同じ数」で「割ってみる」。そうすると、計算結果は1になります。

これで、シュートした回数の項目は全て1に統一されました。
そして、「入った数」を「シュート数」で「割り」ます。
それぞれの試合において、入った数は、その試合にシュートした回数でそれぞれ割っていきます。
そうすると、次のような計算式が出来上がります。

この関係において、シュート数を「もとにする量」、入った数を「比べられる量」と言います。
バスケットボールの試合でシュートした数と入った数を比べることで
まことさんとあきさんのどちらがシュートが上手いか?
ということを考えてみたいわけですが、
「もとにする量」であるシュート数にそれぞればらつきがあるため、公平に判断することが出来ませんでした。

そこで、「もとにする量」を「1」に統一したときの、シュートが入った数、つまり「比べられる量」を比較することで、「どちらの方がシュートが上手いか?」という判断を試みようというわけです。
基準を揃えたら後は比べるだけ!
そして、実際に計算した結果が次のようになります。

この表にある、入った数を比べると、
1試合目は、まことさんは、0.42、あきさんは、0.375。
2試合目は、まことさんは、0.66、あきさんは、0.50。
3試合目は、まことさんが、0.57、あきさんは、0.41。

こうして、それぞれの試合で比較してみると、まことさんの入った数が大きいことがわかります。したがって、どちらの方がシュートが上手いかという問いに対して、まことさんの方が上手いという結論が導かれるわけです。
もともと、シュートした回数がバラバラで、
どちらの方が上手いのかを公平に判断出来なかったわけですが、
こうして「もとにする量」を統一した上で、
シュートが入った数、つまり「比べられる量」を比較することで、
どっちがシュートが上手いかを判断出来るようになります。
割合とは…

この時の、もとにする量を 「1」 と見たとき、比べられる量がどれだけにあたるかを表した数を「割合」 と言います。
従って、全体割る部分が割合というのは、
このように単純な数字の大小関係では比較出来ないときに、
基準とする量、つまり「もとにする量」を統一した上で、
比べたい量を比較する時に利用するものであるということです。

もとにする量を統一するとは、「もとにする量を1にしてやる」ということです。
そして、全体割る部分というのは、「比べる量をもとにする量で割る」ことに該当します。

そうして求めた値が「割合」です。
割合の計算について
さて、それでは実際に割合の計算について、いくつか確認をしていきます。


1番2番は□の中に入る数字を考えます。そして、3番では問いへの解答を考えていきます。
割合の問題では、文章を読んで、どれが「もとにする量」や「比べられる量」で、どれが「割合」なのかを理解しないといけません。
初めて学習する小学生だったり、割合の計算が苦手だと、この辺りの分類で躓くことがあるので、問題を解くための一定のルールについてお伝えします。
割合の問題を解く手順
割合、もとにする量、比べられる量には、3つの見分け方があります。

「1つ目が「~倍」が割合」、2つ目が「「の」の前の□がもとにする量」、3つ目が「残った〇が比べられる量」という見分け方です。

実際にこの3つの手順を踏まえて、問題を見ていきます
56kgは80kgの□倍である。
最初の問題ですが、見分け方の1つ目は「~倍が割合である。」なので、□倍に入るのが割合です。
だから、ここでは割合を求めなければいけないことがわかります。
割合を求めることがわかったら、次は56kgと80kgのどちらがもとにする量で比べられる量なのかを判別することになります。
そこで、2つ目の「「の」の前の□がもとにする量」のルールを適用すると、
□倍の前に「の」があるので、80kgがもとにする量であることがわかります。
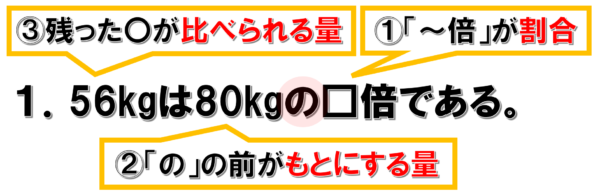
そうすると残った56kgが比べられる量になるので、これで割合が求められます。
したがって、割合は、56÷80は0.7となり、□に入る数値は0.7となります。

それでは、2番目の問題を見ていきます。
□円の0.75倍は30円です。
これも1番目の問題と同じように見分け方のルールを適用してみます。
そうするとこうなります。

したがって、求めないといけないのは、「もとにする量」なので、これを計算すると…

最終的に30を0.75で割って、40となります。
くもわの図
ここで、「くもわ」の図を紹介します。

先ほどの問題で、もとにする量を割合で割るという計算を行いましたが、割合の計算を行う時に、「どれとどれを割り算して、どれとどれをかけ算したらいいのか?」がわからなくなる時があります。
そういった時に、「くもわ」の図を覚えておくと計算に困らなくなります。

「くもわ」の図は、「く」が上にあって、そのしたに「も」と「わ」があります。
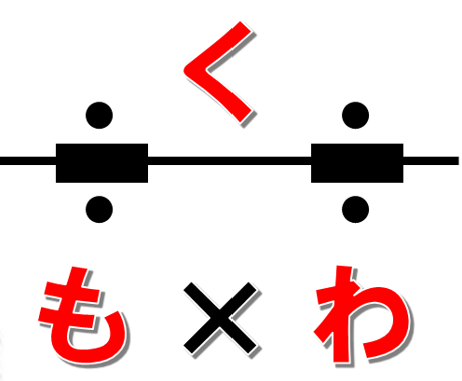
「く」が比べられる量で「も」がもとにする量。「わ」が割合です。
この図の使い方ですが、割合の問題が出てきたら、くもわと図を書きます。
そして、求めたい量を指で隠します。
例えば、割合を求めたかったら「わ」の部分を指で隠します。

そして、残った、「く」と「も」を割り算すると割合が求まります。
比べられる量を求めたかったら「く」の部分を指で隠します。

そして、残った「も」と「わ」をかけ算すると比べられる量が求まります。
このように上と下であれば割り算、横同士であればかけ算すると覚えておくと
計算に迷わなくなります。
もとにする量を求めたかったら「も」の部分を隠します。

すると、上に「く」があって下に「わ」があるので、割り算します。
こうして機械的に計算出来るようにしておくとスムーズに計算が進められます。
それでは、引き続き3番目の問題を見ていきます。
3番目の問題
これは、クラス全体の0.3倍にあたります。
クラス全体の人数は何人ですか?
という問題です。
先ほどの問題よりも、文章が長く一見したところ、1番と2番のようなルールが利用出来なさそうです。

この問題では、多少の国語力が必要になってきます。
まずは、文章の内容を読み解いていくと、求めないといけないのは3行目にある通り、クラス全体の人数です。
そして、2行目を見てみると、「これは、クラス全体の0.3倍にあたります。」とありますが、
「これ」というのは、「1年1組の生徒は45人」という部分にかかっています。
そこで、2行目の内容を書き換えてみると…
![]()
となります。
この文章に対して、割合計算のルールを考えていきます。
そうすると、次のようになります。

これより、クラス全体の人数というのは、もとにする量であることがわかります。
したがって、もとにする量を求めると、
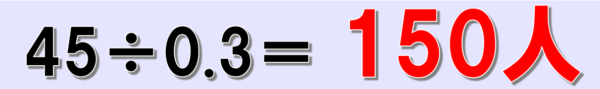
45÷0.3で150人が、クラス全体の人数であることがわかります。
これで「割合とは何か」ということと割合の基本的な計算について見てきました。
次回の記事では、割合についてもう少し詳しく見ていきます。
□次回の記事















