目次
はじめに
今回は回路をテーマにしていきます。
前回までに、クーロンの法則やコンデンサーというものを学んでいきました。
□前回までの記事
今日はまず最初に抵抗の話をして、そして、その後にコンデンサや抵抗を含んだ回路。

さらにスイッチの切り替えを行った時に、どういう風な電荷の動きをするか!?
というような問題にまで対処できるだけの実力をつけるための講義という風に考えてください。
どうしても、回路の問題が苦手な人っていうのは、ただ単独でコンデンサーが1個あったり抵抗が1個か2個つながっていたりという問題からスタートしがちなんですが、そういう問題からスタートしてしまうと…

回路っていうのは、はっきり言って出題者からしてみれば、どんな形でも作れる訳です。
どんなところにスイッチ入れても構わないし、どんなところに抵抗を入れても構わない。

だから解き方を覚えるんじゃないですよ。
確実に解ける!

なぜ、そうやって解いていくのかもわかる。説明ができる!
という状態にしておくとということが非常に大切になる訳ですね。
ですから、もちろんいきなりそういった問題から入るわけではなくて、まずはテーマとして回路の解法ということを述べていきます。
ただし、コンデンサーについては以前の講義でほとんど述べた訳です。
けれども抵抗についてまだ述べていませんから、

まず最初に抵抗について説明をしながら段々と回路の方へ話を持っていきたいと思います。
主題14:回路の解法①(オームの法則)
さあ、それでは主題の14番目になります。
回路の解法をやっていきましょう。


オームは、かけた電圧に比例した形で電流が流れるということを見つけて、その比例定数を抵抗という風に呼んだわけですねぇ。
実験式ですから、これはいきなり書いても構いません。
V=IR。RIと覚えている人もいるかもしれません。それは構いません。

言ってみれば、かけた電圧に比例した形で電流が流れる。
その比例定数がRである!

しかしその比例定数というのは、なぜ抵抗を表しているか!?
ということ。その理屈も考えていきましょう。

例えば、V=IRのVが一定値だったとしましょう。
10ボルトなら10ボルトというふうに決められているとします。その時に電流がたくさん流れた場合は、要するIが大きい時にはRは小さいということになるんです。

電流がたくさん流れると、その比例定数は小さくなります。
ということは、

常にV=IRのRというのは流れにくさの度合い。つまり、Rが小さければ一杯流れるよ。大きければあまり流れないよ。
という式になっています。
オームの法則は、発表当初、日の目を浴びることがなかった。

実はこのオームの法則というのはですね、少しばかり不遇な法則で、これを発表した時に、あまりにも単純な式であることが災いしたのか、ドイツの学会では、大してその重要性が認められなかったんです。
こんな実験的なものっていうのは、役に立たない!
と…

現在の物理学は、理論も重要。実験も重要。
そしてそれが合致することが更に重要。
というような考え方をしています。
けれども、当時は
こんな実験的なことは、しょうもないことだ!

その為に、この式が日の目をみることがありませんでした。このV=IRが発表されたのは、まだ電化が進んでいない時代でした。
しかし、これからさぁ電化をしようという頃に、要するに電線を引っ張っていって、各家庭に、工場とかに、電気を送り込もうというような計画が実行されていくわけです。
一体どのぐらいの電圧で発電所から電気を送り出せばいいのか!?
そうすれば、どのぐらいの電圧で家庭に電気が送り込まれていくのか!?

それにはどうしても、この式が必要になってくるんです。
これすごい式だ!
これが分かれば、どこにどんな電流が流れ、どこにどんな電圧がかかっているか全部計算できるじゃないか!?

これは素晴らしいことだ!
要は、
どのぐらいの電圧で送り出してあげれば、どのぐらいの電圧が各家庭や各工場に届くか!?

ですから、これは素晴らしいことなんです。
凄い式じゃないか!?
一体誰なんだこれ。オームっていう人は??

そうして彼が発表した約14年後にオームの法則は、日の目を見るようになりました。

単純が故に、一時期不遇だった…!
と言うんでしょうか…。
抵抗Rに関する式
さらに彼は、この抵抗Rに関して、こんな式を作っています。


このローっていうのは抵抗率と呼ばれて、単なる比例定数です。
そう思って下さい。

l、lengthですね。抵抗線の長さです。
要するに抵抗線が長ければ長いほど、それだけ抵抗は大きいよと。
それは定性的に何となくわかりますよね。

通りにくいものが、左なのか、右なのか!?
それは、右の方が通りにくいですよね。
長さに比例をするということですね。

このSていうのは、よく面積で使いますよね。
この面積、何の面積かって言うと、導線の面積なんです。

その線の面積に反比例しますよ。
太ければ、要するに面積が大きければ、それだけ抵抗が小さいんですよ。

これは、どうイメージすればいいでしょうか…??


1車線道路と4車線道路では、どちらが多くの車は移動できますか??
もちろん4車線道路ですね。
道路の幅が広ければ広いほど、たくさんの車を通ることができます。
それと同じことです。

ですから、Sが大きければ大きいほど、それは道路が広いことに相当する訳ですから、それだけ抵抗は小さい!
流れやすいということになるわけです。

確かに電荷の流れなんて私たちには見えないわけですが、「水の流れや車の流れなど、何かに例えて式を理解しておく。」ということは非常に重要ですから、今のような例を挙げておきました。
抵抗に関するエネルギーの式

それではもう1つやっておかなければいけないことがあります。
それが何かと言うと、このエネルギーに関する式です。
今、抵抗線があるとします。

そこに電流が流れてくる。


抵抗っていうのは、流れにくい訳ですよね。
ですから、流れようとしても思うように流れることができない。

ということは、どういうことか!?

それだけ電気的なエネルギーが失われてる!
ってことなんです。

抵抗のせいで。
抵抗は越えようとすると抵抗してるわけですから、それだけエネルギーが失われてしまう。

じゃあ、その失われたエネルギーって、何になるの!?

実は熱になるんです。
ジュール熱と呼んでいます。ジュールって言うのは人の名前です。


オーブントースターでパンを焼く時、この熱を利用しています。
というと、分かりやすいと思います。

電化製品の多くっていうのは、熱が出てくることが多いですねぇ。

いやそんなことはない。

冷蔵庫なんか冷たくなるじゃないか!?
っていう…

そんな人は冷蔵庫の裏を触ってみてください。
暖かいですから。
要は、電気を流して何か仕事をさせようとすると、どこかで熱が出てしまうんです。
思い通りに抵抗をゼロにする!

「こういうことが起きる。」というのをジュール熱と呼んでいます。

これを一体どのように計算すれば良いんだろう?
って訳ですね。
実は、簡単なんです。

それは、なぜかって言うと、ちゃんと勉強してきたからなんです。
書いてみましょう。

一般にPで表します。
(消費)電力と言われてます。
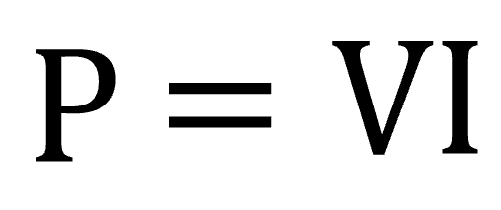

もちろんVというのは、抵抗の両端にかかっている電圧です。
それにIを掛け算する。

なぜか!?
Iアンペア流れているということは、1秒間当たりIクーロン流れている。

Vというのは、1クーロンあたりの位置エネルギーでした。
じゃあ抵抗では、どういうことが起きるかっていうと、

1クーロンあたりVだけ消費する。

それで、Iクーロン流れてるんです。
それならVIでしょう。
例えば、1クーロン流れてくれば、それはVです。

3クーロンだったら3V消費することになる。


IクーロンだったらI掛け算すればいい。
ただ、それだけのことです。
ところが、オームの法則V=IRが成り立っています。
V=IRということは、
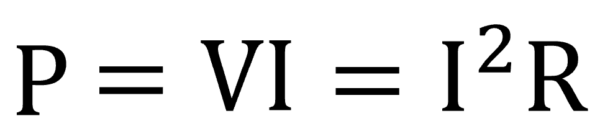 と書くことができます。
と書くことができます。
V=IRが成り立っています。
ということは、IはR分のVです。
したがって、こうなります。
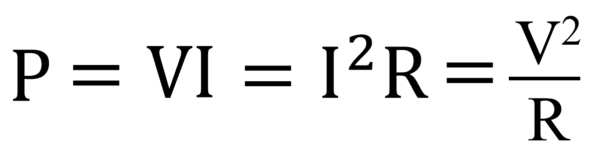
消費電力と呼ばれています。

ワット(W)という単位で書くことが多いですねぇ。

続けていきます。
こちらの式(W=VI)は、VとかIとか、電流とは何かという定義から分かるものです。

ですので、いずれの式も非常に大事なんですが、

V=IRとR=…の式は、記憶しても構いません。
しかし、W=VIは自分で意味を考えながら、書けるようにならなくてはいけません。
コンデンサーとの比較

これで、もう抵抗についてはほとんど話が終わったわけですが、前回の講義を思い起こしてください。
参考としてせっかく抵抗についてやったんですから、コンデンサーについてやってみることにします。
もう既に皆さんも知ってる式です。
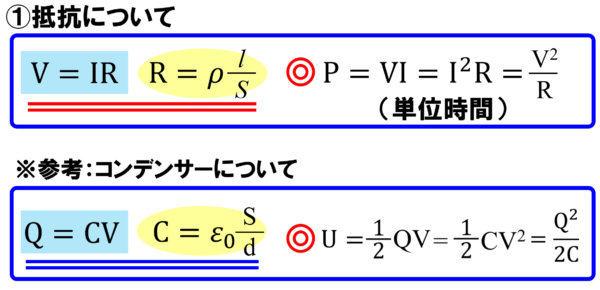
上が抵抗です。下がコンデンサーです。

皆さんの頭の中で、こういうセットになっているでしょうか!?

ただし、P=の方は単位時間です。U=の式は単位時間じゃないです。
だから、Pはワットという単位で、Uはジュールという単位です。
こんな感じで
抵抗は抵抗でこういう式を持っている!
コンデンサーはコンデンサーでこういう式を持っている!
ですから、決して回路の問題っていうのは難しくない。

ただ、皆さんにここで勘違いしてほしくないことがあります。

そんなの先生知ってます!
こんなのみんな覚えてます!
…と。

でも回路は苦手です!
っていう人がいるんです。

そこが大問題なんです。
式は全部知ってます。でも回路が苦手になる!

多分…、知ってるけど回路が苦手っていう人は、知ってるというよりも丸覚えしただけで、「いったいこれが何なのか!?」がわかってないですね。
そのせいで、これをどう使って良いかわかんないんです。
今、回路が苦手だと思っている人が、例えば回路の問題を問題集で解くとします。
うまくいかない。
うまくいかないとみんな解答をみます。

その解答を見ても分からないですか??

そういう人は、少ないんじゃないですか??
これらの式が頭に入ってる人は、解答を見れば分かるです。

なるほど、そうやって解くか!?
って。

そういうのはこれが頭入ってるから、そのように思えるんでしょう。
式が頭入ってないと、「なるほど!」って思えないですから。
ところが…、自分で解こうとするとなかなか上手くいかないんです。

それは結局は知ってるけど、この式の使い方がイマイチわかっていない!
ということになってきます。

それでは、これをどう使えばいいのか!?
ということです。

こういうエネルギーに関する式というのは、「エネルギーを問われたときとか、仕事を問われた時にやれば良い。」ということは、それはまあいいと思うんです。
ところが回路の中で、
どれだけの電流が流れていますか?
どれだけ電荷が蓄えられましたか?
さらに
コンデンサーの極板を広げました。
コンデンサーの間隔を広げました。
抵抗の線を半分に切りました。
抵抗線を倍伸ばしました。太さを変えました。

まずは、その整理が必要です。
そうやらないと、どこからスタートして良いかが見えなくなってくるということです。

ですから、ただ丸覚えじゃなくて、何のための式なのかということを頭の中にちゃんと整理しておくんです。
覚えた式をごちゃごちゃに頭の中に入れてくんじゃなくて
この式は、こういうことをするためのもの。
この式は、こういうことをするためのもの。
という形で、まずは整理していくことです。

…

それだけでは解けませんよね。

それは私もわかってます!

コンデンサなんかでスイッチをカチャカチャ切り替えられたらもう解けません!
っていう人がいます。

それは、もうあんまり心配することないです。
こういうものを、いかに使うかってことが分かってないからです。
■コンデンサーの問題演習(制作中)■





















