目次
はじめに
今回は仕事と力学的エネルギーについて、基本事項を確認しながら問題演習に重点をおいて解説していきます。
基本事項の詳しく知りたい人は、前回の記事を参考にしてください。
ここでは仕事と仕事の原理を中心に進めていきます。
基本事項の確認
まずは仕事の定義からです。

高校物理における仕事の定義は、次のようになされています。

このとき計算される仕事の単位はJ(ジュール)を使用します。
仕事量の計算(例)
この定義に基づいて考えていくと、実際には次のように考えることができます。
①まずは、物体に力Fを加えて、力を加えた方向にx[m]移動させる場合です。
このときの仕事Wは、W=Fx となります。

もしも物体に力を加えたとしても、物体が全く移動しなかったらF×0で0ジュールとなって、この時、力は仕事をしていないと解釈します。
②次に、物体の進行方向に対して、θの角度をなす力を加える場合、この時の仕事については、力Fを進行方向の成分に分解して計算します。

したがって、WはFcosθ×x です。
一方、進行方向に対して垂直な力の成分ですが、この力は、物体をx[m]移動させることには関与していないと解釈します。
したがって、進行方向に対して常に垂直な方向にはたらく力がする仕事は0という風に考えます。
③そして、最後に、進行方向とは逆向きにはたらく力がする仕事は、物体が移動することに対して、邪魔をしたという風に考えます。

したがって、この場合の仕事については、マイナスをつけて負の仕事量として表現します。
問題解説
ここまで確認したところで実際に問題を見ていきます。
問題1
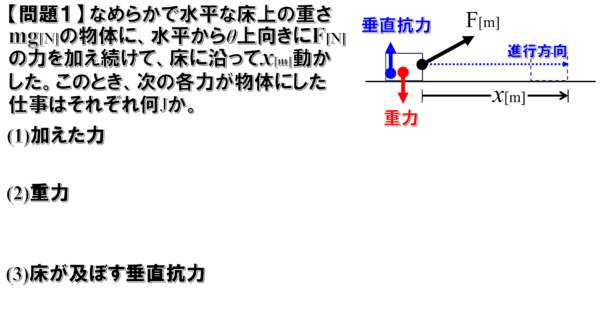
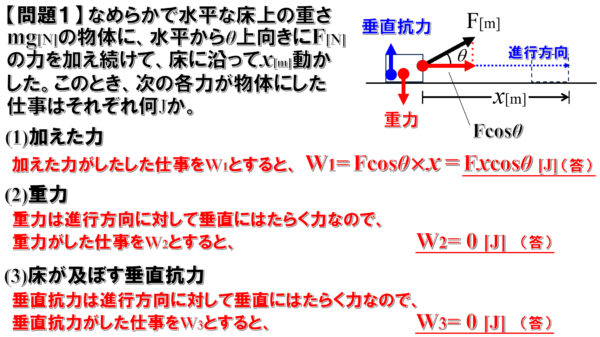
(1)
この場合、加えた力がした仕事をW1として、進行方向の成分だけが仕事に作用したと考えると、
W1=Fcosθ×x=Fxcosθ
となります。
(2)
次に重力がした仕事ですが、これをW2とすると、重力は進行方向に対して常に垂直にはたらく力ですから、この場合の仕事は0
(3)
同様に床が及ぼす垂直抗力がした仕事についても、これをW3とすると進行方向に対して垂直にはたらく力ですから、この場合の仕事も0です。
では、次の問題に進みます。
問題2
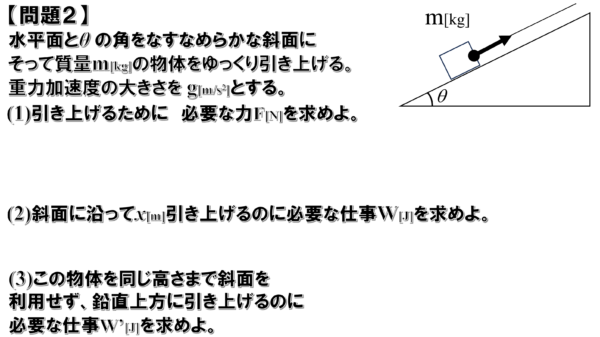
(1)
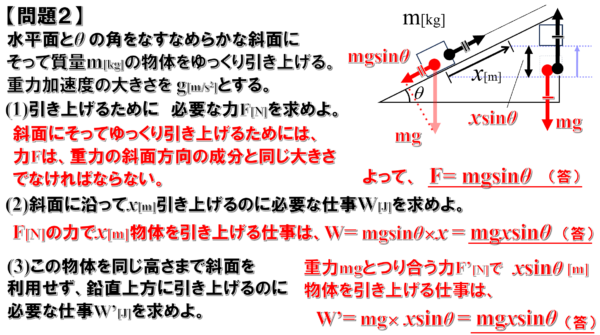
この時、引き上げるために必要な力Fですが、問題文に「物体をゆっくり引き上げる」とあります。
これは、物理の問題特有の表現になりますが、ここでは「物体にはたらく力のつり合いを保ったまま移動させる。」という風に解釈してください。
したがって、物体にはたらく力を作図したときに斜面にそってゆっくり引き上げるためには、力Fは重力の斜面方向の成分と同じ大きさでなければならないと考えて、力Fを求めます。
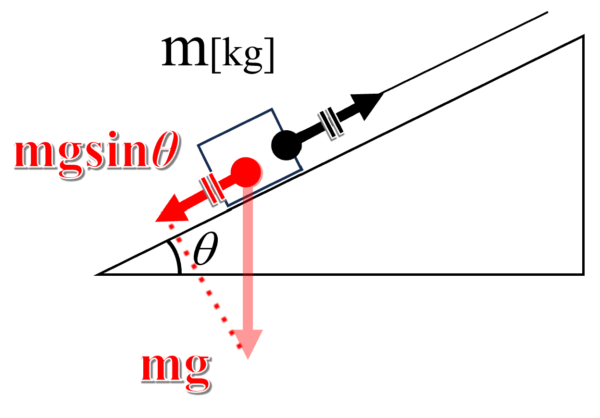
したがって、重力mgを斜面方向と斜面に垂直な方向に分解すると図のようになるので、物体を引き上げるために必要な力Fは、mgsinθとなります。
(2)
次に斜面にそってx[m]引き上げるのに必要な仕事ですが、(1)で求めた力で、ゆっくりと x[m]移動させたらいいので、
この時の仕事Wは、Wイコール、力がmgsinθで、かけることの移動した距離がxとなって、
これより、mgxsinθ となります。
(3)
最後に、斜面を利用せずに、鉛直上方に引き上げるのに必要な仕事ですが、斜面に沿ってx[m]移動させたとき、物体はxsinθ[m]だけ鉛直上方に移動します。
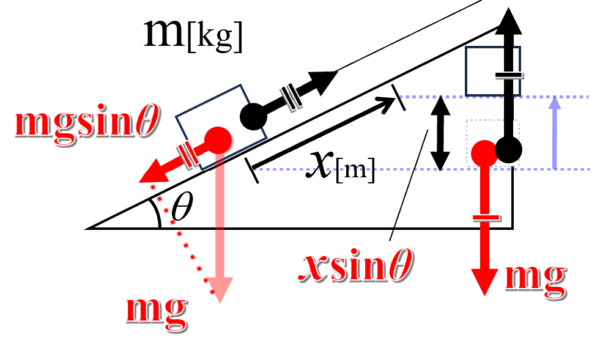
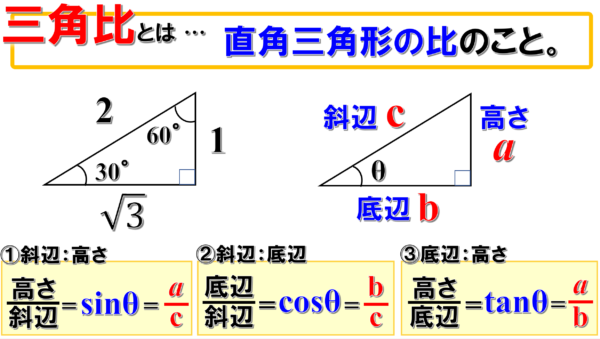
sinθの定義は、斜辺分の高さです。斜辺分の高さがsinθになるためには、高さがxsinθでなければなりません。
これと同じ高さだけ引き上げるということですが、重力mgとつり合う力でもって、xsinθ[m]移動させるわけですから、
この時の仕事W’は、W’イコール、力はmg、かけることの移動距離はxsinθとなって、これよりmgxsinθ となります。

2番と3番は同じ結果になっています。
(2)では、斜面を利用する分、引き上げるのに必要な力が小さくなる分、動かす距離は長くなっていて、
(3)では、
動かす距離が短くなっている分、引き上げるのに必要な力が大きくなります。
これを仕事の原理と言って、斜面や滑車などの道具などをつかうと、物体を引き上げるのに必要な力が軽くなりますが、動かす距離は長くなるので、結局のところ必要な仕事量は同じであるということを意味しています。
問題3

仕事率を求める問題です。
仕事率とは、単位時間当たりの仕事のことで、SI単位系では、1秒あたりの仕事のことを指します。
要は仕事の効率を評価するための指標のようなものです。
この定義に沿って、問題の解答に移っていきます。
問題文には表記されていませんが、リフトを使って持ち上げるので、ゆっくりと物体が上昇していくと考えて解答します。
したがって、リフトは物体に対して常に重力と同じ大きさの力Fで、ゆっくりと x[m]持ち上げたと解釈すると、
仕事率はPイコール、持ち上げた時間はt[s]、それ分の力は重力と同じ大きさと考えてmg×持ち上げた高さはx[m]、したがって、これを計算すると、
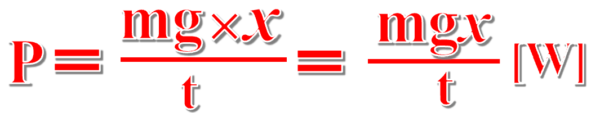
となります。
問題4

抵抗力の大きさを求めないといけないのですが、唐突に「抵抗力」というフレーズが出てきているので、解法の糸口が掴めません。
そこで、まずは問題の状況について詳しく見ていきます。
今、車は推進力F[N]を受けています。その結果、一定の速さvで走行します。
とりあえず、ここまでの状況を図に整理しました。
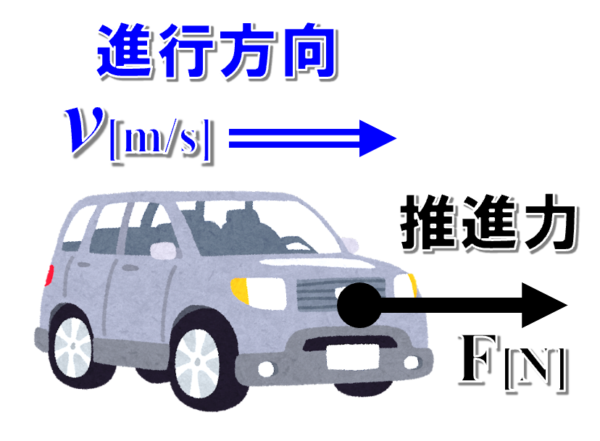
しかしながら、力は、物体の運動状態を変化させるものです。
図の状態だと、右向きに推進力Fが働いているわけですから、このままだと、車はどんどん加速してしまいます。
したがって、車が一定の速さvで走行するためには、左向きにF[N]の力を受けないといけません。
この問題では、左向きの力が抵抗力であると考えます。
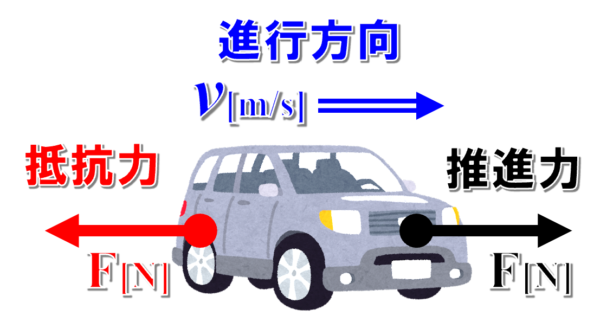
止まっていた車が、エンジンをかけて、F[N]の推進力で動き始めます。
すると、車はどんどん速度をあげていくわけですが、速度が上がる度に、空気からの抵抗力が増していきます。
そして、速度がvになったところで、車の推進力と抵抗力が等しくなって、車は一定速度で走行するようになったのが、問題文で与えられた状況だと考えて下さい。
そうすると、車の受ける抵抗力の大きさはF[N]となって、エンジンの仕事率ですが、
仕事率は、力F、移動距離x、時間tを使ってt分のFxと書けます。

しかし、今回はtもxも与えられていません。
そこで、t分のFxを良く眺めてみて、どうすれば良いのかをよく考えてみると、t分のxという部分に目が入ってきます。
t分のxという計算式ですが、速さを求める時に、距離÷時間で計算したことを思い出してください。
そうすると、t分のxも距離x÷時間t
つまり、単位時間当たりの移動距離となっているので、この部分は、速さvに置き換えることができることに気付きます。
したがって、エンジンの仕事率は、Fv [W]となります。

それでは、次の問題に移ります。
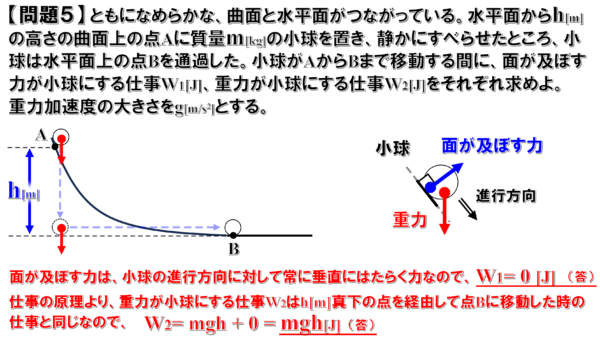
問題5

ここでは、曲面上の点Aから小球をすべらせて水平面上の点Bを通過する時に、面が及ぼす力がする仕事と重力が小球にする仕事を考えます。
それぞれ別々に見ていきます。
その前に小球にはたらく力を整理しておきます。そうすると、小球には、地球の中心に向かって、つまり下向きに重力と曲面上からの垂直抗力がはたらくことがわかります。
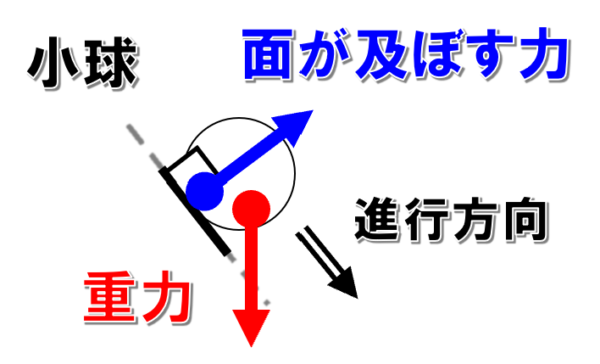
この問題では、垂直抗力のことを「面が及ぼす力」と表現していることに注意してください。
したがって、面が及ぼす力は曲面をすべっている間は、常に進行方向に対して垂直にはたらきます。
したがって、面が及ぼす力がする仕事W1ですが、
面が及ぼす力は物体が移動するという事には、関与していません。したがって、W1は0[J]となります。
次に重力がする仕事W2です。こちらについては、W=Fxの式を使って計算することができません。
高校物理の範囲では、計算によって求められる仕事は、
「一定の力F[N]を物体にはたらかせて、力の向きに距離 x[m] だけ動かした時の仕事」
だけですが、
ここでは、重力の進行方向の成分が一定ではありません。
さらには、小球が移動した距離を問題の条件から求めることが出来ません。
したがって、これとは違った方法で仕事を求めないといけません。

そこで、問題2でやったことを思い出してみます。
問題2では、斜面上の物体を同じ高さまで引き上げるのに直接持ち上げても、斜面を使っても、
必要とする仕事は変わらないということでした。
これを仕事の原理という訳ですが、ここでも仕事の原理を応用してみます。
すると、点Aから点Bまでに、小球にはたらく重力がした仕事は、曲面を下ろうが、直接下ろうが変わらないという風に考えることができます。
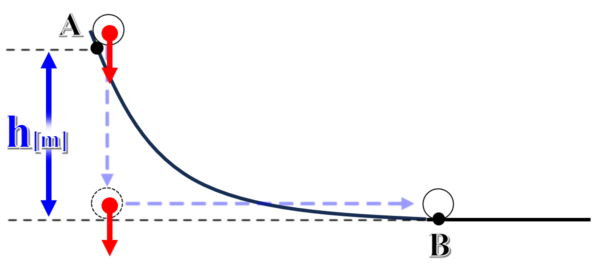
この時、点Aから真下に落ちて、それから点Bに移動する場合ですが、重力は、h[m]落ちるまでには、力mg×距離h [J]の仕事をして、それから真下の点から点Bに移動するまでは、力は、常に進行方向に対して垂直の関係にあるので、この区間の仕事は0。
したがって、小球にはたらく重力がした仕事W2は、W2=mgh+0 で計算すると、W2=mghということになります。
それでは、今回の解説は以上です。
次回は、仕事とエネルギーの関係に関する問題解説を行います。

















