目次
はじめに
今回は位置エネルギーについて見ていきます。
高校物理で学習するエネルギーについては、運動エネルギーと同じように位置エネルギーというものがあります。
位置エネルギーには、重力による位置エネルギーと弾性力による位置エネルギーがあります。
重力による位置エネルギー
その中のまず1つ目。重力による位置エネルギーから進めていきます。

重力による位置エネルギーっていうとね、こう考えてください。
落下能力!!
落下能力と考えると分かりやすいです。
落下能力について
例えば、ここにボールがあります。


このボールはテーブルの上に置いてあるから落ちないんです。
置いてあるから落ちない。
しかし、このボールを私が持ち上げるとします。
ボールを持ち上げる

手を離すと落ちる

そうすると、手を話せば落ちます。

何を当たり前のことを言ってんだと思うかもしれませんが、テーブルに置いているときには、ボールは落下能力を持ってないんです。
ところが、ボールを持ち上げた時は、ボールは落下能力を持っているんです。

手を離せば落ちるんです。
テーブルの上だと、手を離しても落ちません。

ということは、このボールがテーブルに置いてある時と、手で持ち上げた時では、ボールにとっては能力が違うんです。
上にある方が、それなりの落下能力持ってるんです。

これを位置エネルギーといいます。
位置が違うことによって持つエネルギーのことです。これを位置エネルギーといいます。

しかし、所詮はボールです。ボールが勝手に能力を持つわけないんです。

誰が能力を持たせたの!?

それは私です。
私が、よ~いしょって、ボールを持ち上げたんです。
その時に、ちゃんと仕事をしました。

仕事をしたせいで、ボールが落下能力を持った。
こういう考え方です。
重力による位置エネルギーの式
テーブルの上にボールが置いてある。

ところが、それを私は手で掴んで上向きに力Fで高さhのところまで、よいしょって持ち上げたんです。
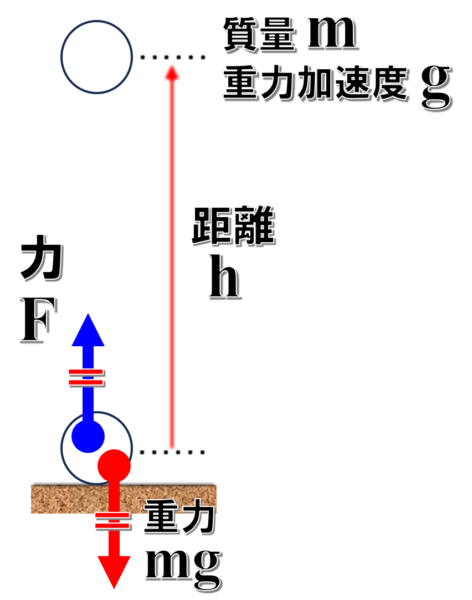

そうすると私のした仕事…、力Fのした仕事はどうかけるか。
Wイコール力Fを加えてhだけです。
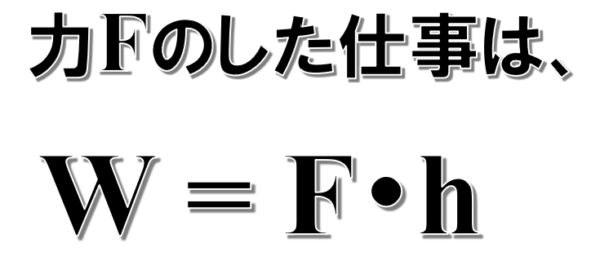

ただそれはゆ~っくりと持ち上げたと考えてください。
ここで速度vを持っている必要はないので、力のつり合いが保たれたまま、ゆっくりと持っていくと考えてください。
そうしたら力のつり合い保ったままなので、Fとmgは等しいとしてこれだけの仕事をした。
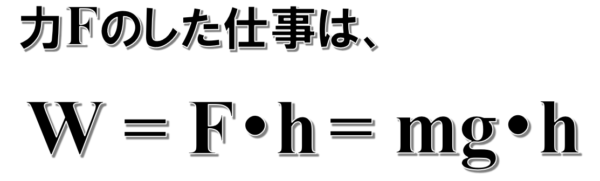
簡単に言うなら、力mgに逆らってhだけよいしょって持ちあがった。
持ち上げた私はしんどかった。

あぁ~、しんどかった~…
って言って
それだけの仕事をした結果どうなったか?

その結果、ボールを落下能力を持ったんです。
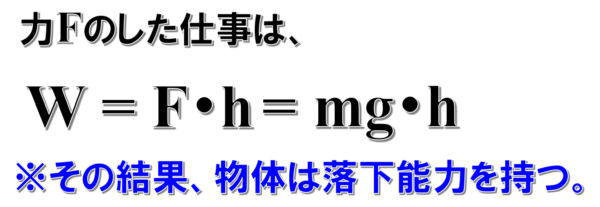
この落下能力のことを位置エネルギーと呼んでいます。

重力による位置エネルギー
即ち、Uで表わすことが多いんですが、mgh

これが重力による位置エネルギーです。

要するに、どのぐらいの力を加えてどのぐらいまで持っていったか!?

あーしんどかったぁ・・・

そんな仕事をしたから、その仕事分だけ物体は落下能力を持ってくれたってことになるわけです。
弾性力による位置エネルギー
それでは、もう1つ行きます。

もう1つ力学の中でよく出てくるのが、弾性力による位置エネルギーです。
これは簡単に弾性エネルギーと言ったりもします。
ばねを考えられればいいです。

これは、さっきのように簡単には行きません。
ここに、ばねがあります。

今の長さが自然長です。
この状態のばねを10センチ縮めるのは簡単です。

ところがね、ある程度ギュ~っと縮めたところで、さっきと同じ10センチ縮めるのは、とてもしんどいです。

ばねは力が一定じゃないんです。
さっきのようにボールを上に持ち上げて落とす時は、ず~っとmgに逆らっていたらいいだけでした。

ところが、ばねは場所によって強さが違うんです。

どうすればいいの??

こうするんです。
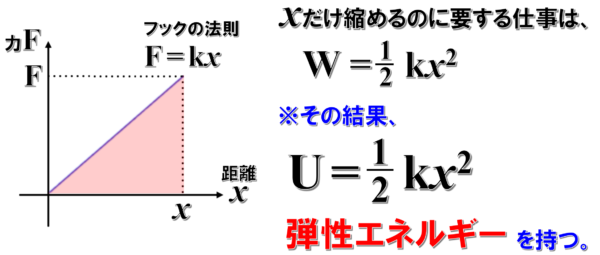
ばねは、フックの法則に従います。だから、力と距離の関係をグラフに書きます。
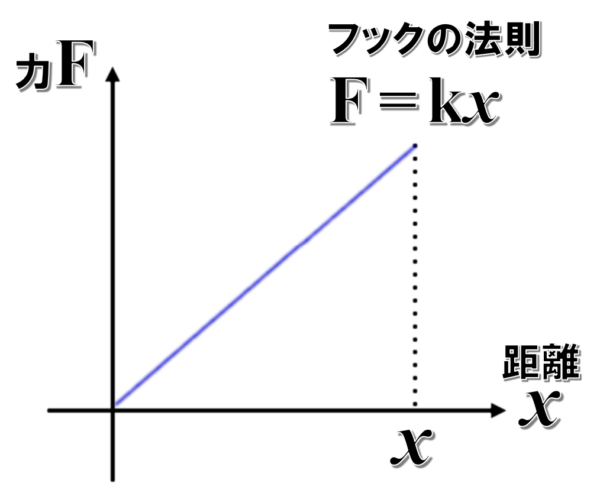
そうすると、F=kxと書くことができるから、原点を通る直線のグラフになります。
その時に、仕事は、この面積で表わされる。
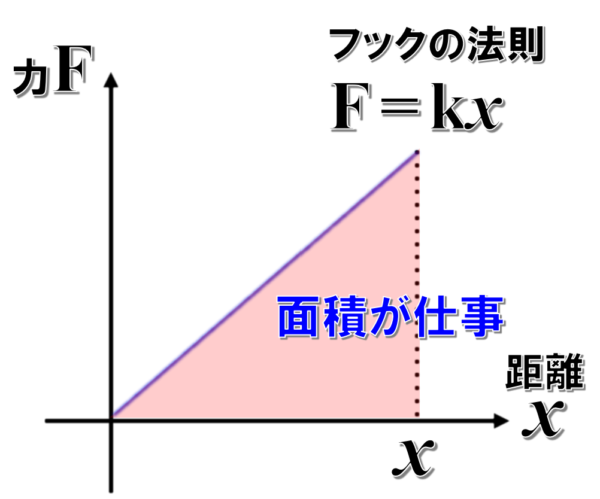

こうする訳です。

なぜ面積なんですか?

それは簡単です。
例えばボールの場合だと、ずっとmgでhまで持っていったんです。その時はmg×hということです。
縦軸を力Fにすると、ず~っと力が一定だったとします。
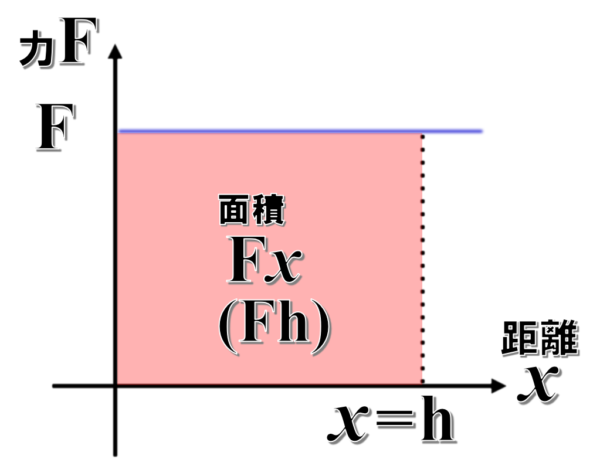
※重力による位置エネルギーの場合F=mgで考えます。
x=hのところまで持ってくると、その時の仕事はFxになります。

この場合も面積です。だから、ばねのときも面積で考えるんです。
グラフを見たらわかると思いますが、最初はほとんど仕事なんか必要ではないんです。
自然長のところだったら、少々縮めるのに大して力はかからない。
ところが、ある程度までぎゅ~っと縮めた所でまた同じだけ縮めようとしたら、とてもしんどいんです。
だから、どんどんどんどん仕事は大きくなる。

そうすると、xだけ縮めるのに要する仕事(F-xグラフの面積)は…

2分の1×底辺×高さ
1/2 F×x。ばねの場合は、Fはkxと書けます。

ということは、1/2kx2です。
ばねをぎゅっと押し縮めるのに、私たちはこれだけの仕事をしなければいけない。

ということは、その結果として、弾性エネルギーU=1/2kx2を持つという考え方ができます。
ばねは押し縮めれば、びよ~んって打ち出すだけの能力持っています。
その能力っていうのは、ぎゅっと押し縮めるときにした仕事に等しいはずだという訳です。

勝手にばねが能力を持つわけがない。だから誰かが、何かしたんです。
誰かが押し縮めたから、ばねは能力をもった。その押し縮める時に加えた仕事分がその能力であると評価できるはずです。

だから、仕事を計算すればいいんです。
こういうことになります。
仕事をしたから物体は、能力、エネルギーを持った。
という風に因果関係があることを忘れないようにしてください。
そういうことも含めて頭に入れてると、式変形はいつでもできるようになっていきます。
練習問題
それでは実際に例題を解いていきます。
例題1解説
質量5.0kgの物体Aが高さ10mの建物の屋上にあり、同じ質量の物体Bが地下5.0mの地下室の床上にある。次の(1), (2)の各場合について、物体Aと物体Bの重力による位置エネルギーUA[J], UB[J]とその差ΔU[J]を求めよ。
重力加速度の大きさを9.8m/s2とする。
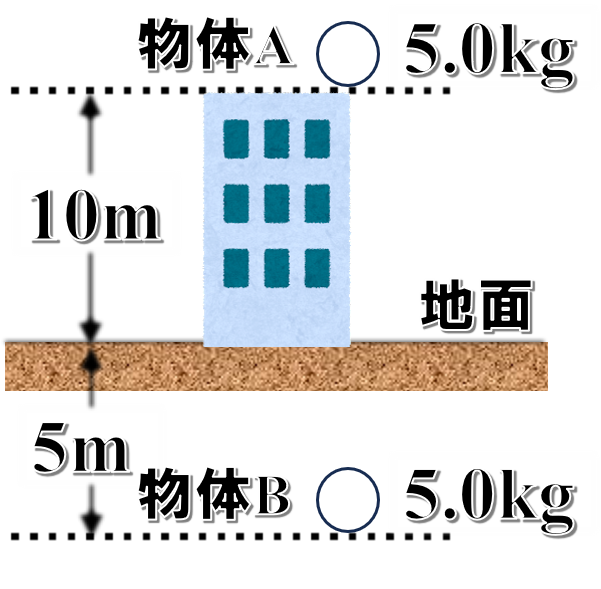
(1)地面を基準水平面としたとき
地面を基準水平面にするということは、今ある物体が地面にある場合と比べて、どれだけ落下能力があるかということです。
物体Aは地面よりも10m高いところにあるので、10m高い分それだけ地面に落下する能力があります。
その落下能力はU=mghの式から、UAは5.0×9.8×10で4.9×102[J]となります。
![]()
一方、物体Bは、地面よりも5.0m低いところにあります。
地面よりも5.0m落ちてしまっているので、それだけ落下能力を使ってしまったわけです。
このように基準水平面より低い位置にある場合の位置エネルギーは負のエネルギーで表現します。
つまり、UBは5.0×9.8×・・・
高さは地面より5.0m低いのでー5.0として
答えは、ー2.5×102[J]となります。
![]()
またUAとUBの差は、ΔU=UAーUBを計算すると、答えは、7.4×102[J]となります。
(2)地下室の床を基準水平面としたとき
今度は地下室の床が基準水平面になるので、地下室の床に物体がある場合と比べて、どれだけ落下能力があるかを考えます。
そうすると、物体Aは、地上まで5.0m
地上から10mの合計15m高い所にあるわけですから、
その落下能力は、5.0×9.8×15で7.4×102[J]となります。
物体Bは地下室の床にあるので、UBは5.0×9.8×0 で0[J]となります。
ΔUは7.4×102から0を引くので、そのまま、7.4×102[J]となります。

それでは次の問題に行きます。
例題2解説
天井に固定したつる巻きばねの下端に質量0.50kgのおもりをつるしたら、ばねは0.070m伸びた。重力加速度の大きさを9.8m/s2とする。

(1)つる巻きばねのばね定数は何N/mか。
つる巻きばねにおもりをつるすと、おもりには下向きの重力とばねの弾性力が作用して、ばねが0.070m伸びたところで力がつり合って静止します。
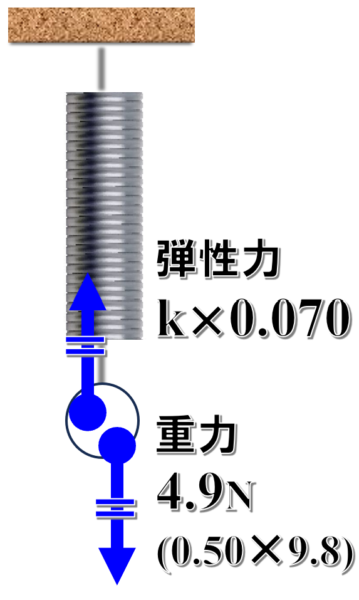
重力の大きさは0.50×9.8で4.9Nで、これがばねの弾性力の大きさと等しいので、フックの法則をつかってばね定数kを求めると、4.9=k×0.070という式より、kは70[N/m]となります。

(2)おもりに蓄えられた弾性力による位置エネルギーは何Jか。
弾性力による位置エネルギーは、U=1/2kx2の式より、Uは、1/2×70×0.072で、0.17Jとなります。

それでは、今回の解説は以上となります。