
はじめに
ここでは等加速度運動の3つの式の使い方を実際の問題を通して確認していきます。
動画による解説はこちら↓↓↓
等加速度運動の式の使い方
物体が、右向きに12m/sの速度で原点を通過した後、右向きに1.5m/s2の加速度で10秒間運動した。このときの物体の速度はどの向きに何m/sか。

物体が原点を通過した時の速度は12m/sなので、初速度v0は12m/sです。そして、右向きに1.5m/s2の加速度で10秒間運動したとあるので、これは速度と時間を考える問題であることがわかります。
したがって、等加速度運動の3つの式の内、v=v0+atの式を利用します。

求めたいのは、右向きに1.5m/s2の加速度で10秒間運動した時の物体の速度です。
これをvとすると、解答は次のようになります。

物体が、右向きに8.0m/sの速度で原点を通過した後、左向きに0.50m/s2の加速度で7.0秒間運動した。このときの物体の速度はどの向きに何m/sか。
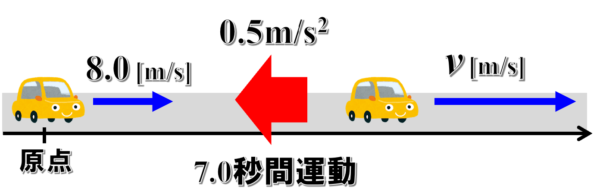
物体が原点を通過した時の速度は8.0m/sなので、初速度v0は8.0m/sです。そして、左向きに0.5m/s2の加速度で7.0秒間運動したとあるので、右向きを正の方向とすると、加速度は-0.5m/s2と表せます。

これはつまり、物体は1秒間に0.5m/sのペースで減速したということです。
そして、ここでは7.0秒間減速した時の物体の速度が問われているので、これは速度と時間を考える問題であり、(1)番と同様に、v=v0+atの式を利用します。
したがって、求める速度をvとすると次のようになります。

物体が、右向きに5.0m/sの速度で原点を通過した後、右向きに3.0m/s2の加速度で4.0秒間運動した。この間の物体の変位はどの向きに何mか。
原点を5.0m/sの速度で通過した物体が、右向きに3.0m/ s2の加速度で4.0秒間運動します。
この時、4.0秒間運動した後の位置をxとして、このxがいくつになるかを考える問題です。

ここでは、物体の変位、つまり、物体の位置が原点からどれだけ変化したかを聞いているわけですから、等加速度運動の式は…
![]()
を利用して、xを求める方針で進めていきます。

そうすると、v0は5.0、tは4.0、aは3.0ですから解答は次のようになります。
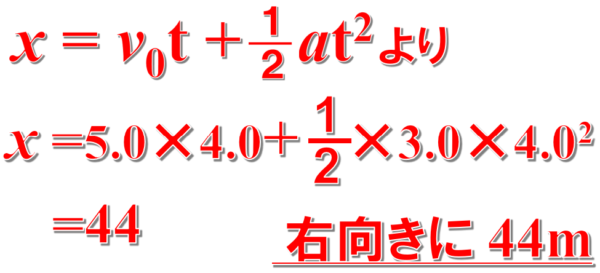
物体が、右向きに3.0m/sの速度で原点を通過した後、右向きに2.5m/s2の加速度で運動し、右向きに7.0m/sの速度となった。この間の物体の変位はどの向きに何mか。
原点を3.0m/sの速度で通過した物体が、右向きに2.5m/s2の加速度で運動した結果、7.0m/sの速度になりました。7.0m/sの速度になるまでに、物体の位置がどれだけ変化したかと聞いています。

ここでは、時間については触れられていません。
したがって、ここでは等速直線運動の式のうち、物体の速度と変位に関する式
![]()
の式を使っていきます。
vは7.0。v0は3.0。aは2.5なので、物体の変位をxとして、この式に代入すると次のようになります。
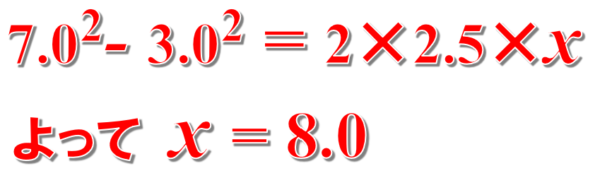
したがって、答えは、右向きに8.0mとなります。
これで解説は以上となります。
この単元の記事
















