目次
はじめに
これから波動について学習していきます。

波の分野は苦手意識を持ちやすい単元ですので、一体どういうことをどういう順番で学習していけば良いのか??
ということを考えながら進めていきます。
1.波動とは、波源の振動が伝わる現象である。
2.波長・振幅、周期・振動数、位相などの物理量、用語を理解する。
3.波の基本式 v = f l の成り立ちを理解する。
※振動数、位相、波の基本式は後編で学習します。
日常生活における波
波動現象というのは、皆さんの生活の中でたくさんあるのですが、なかなか気付きにくいところです。
例えば、携帯電話で通話をするというのは、電磁波という波を利用して、電話番号に紐付けられた電波をキャッチした相手と通信するわけですが…

こういう所は難しい話になってきますので、簡単なところから始めていきたいと思います。
例えば、ロープの一端を固定して、そのロープの反対側を持って、上下に揺らしてみると、簡単に波動現象が観察出来ます。
☝画像をタップすると動画が視聴できます。

この波動現象から観察できる波の性質というものが、これから学習していく様々な波動現象にも共通する性質になっていきます。
したがって、こうして容易に観察することが出来る波からスタートしていきます。
■様々な物理量
今回は次のような内容を学習する予定ですが、波について学習する上で、様々な用語や物理量が登場します。

こういった物理用語がわからないと、次回以降、私が説明していく内容の意味がわからなくなってしまいます。
そこで今回はまず、「波動に関する様々な量」について学習していきます。
1.波動とは

最初に、「波動とは…」一体何なのかということから見ていきます。
図のように、ロープの端を持って、上下に揺らすと、山なりの波形が伝わっていくことが確認できます。


波形が伝わる様子をよく観察すると、手を上下に揺らす振動が、右方向に伝わって行ってる様子が確認できます。
これが波動現象です。

この時、上下に揺らしている部分のことを波源と言います。
波の源と書きます。
今、波の源が揺れているわけです。
その振動が、伝わっていくだけ。
これが波動現象です。

つまり、「波動現象とは波源の振動が伝わる現象です。」
これは非常に大切なことなんですが、

波動とはこんなに単純なんだ!!
ということが理解していただけると思います。

高等学校で扱う波源の振動は単振動と言います。
■参考:単振動
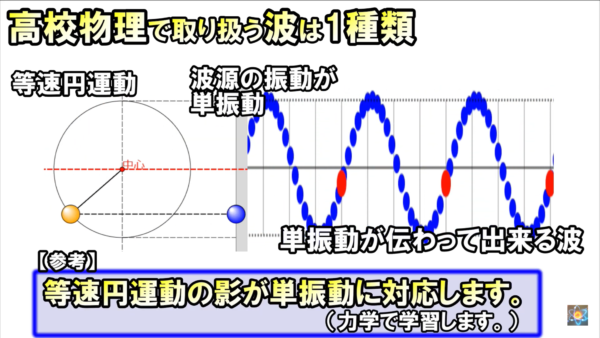
ただ上下に一定のペースで行って帰ってくる非常に単純な振動で、尚且つ等速で伝わるものだけを扱っていきます。
■参考:等速円運動
したがって、

波動って一体何??
と聞かれたら、

波を作るところがあって、それが揺れている。その揺れがどんどんどんどん まわりに伝わっていく現象のことを言うんですよ。
と答えれば言い訳です。

そして、一般に光を覗いて振動を伝えるためには伝わるものが必要です。
そのもののことを媒質と言います。
例えば、ロープとか、水面を伝わる波であれば水とかが媒質になります。

従って、

波動とは、ただ振動が伝わっていくだけであり、振動を伝える物質のことを媒質と呼びます!!
単純に答えられることが大切になってきます。。
それでは、今度は波の具体的なところに入っていきます。
2.「変位」、「波長と振幅」 について
これから、2つの用語を押さえていきます。

それが波長と振幅です。
波長は、一般的にギリシャ文字でλと書きます。

振幅…、一部では振れ幅と言ったりすることもありますが、振幅で説明していきます。
Amplitudeの頭文字をとって、Aとかaで表現します。
両方とも長さを表す量です。

今から早速、図を確認しながら「波長とは何か?」、「振幅とは何か?」を考えていきます。
まず図のように一端が固定されたロープを揺らします。

そうすると波が出来ます。
その時に、ロープの振動は画面のように伝わっていったとします。
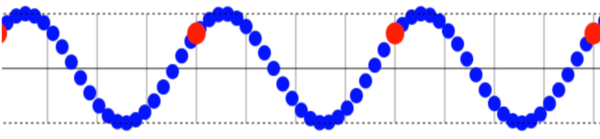
黒の実践部分は、ロープがもともとあった位置だと考えてください。
変位について
この時、図の矢印で示すような場所は、元々の位置に対して変化していることが確認出来ます。
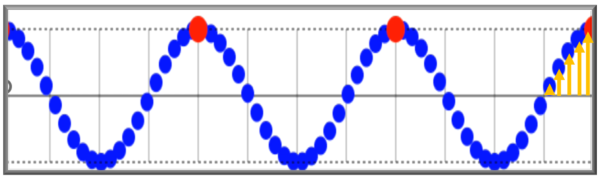
このような位置の変化量のことを変位といいます。

変化する位置と書いて変位です。
もともとロープがあるところから現在あるところまでが変位です。

したがって、上向きを正(=正の変位)とした場合、こういう場所は「変位が負である(=負の変位)!」という風に書きます。
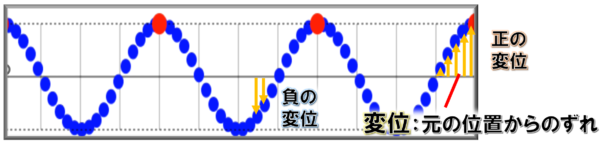
変位という言葉を覚える必要はありませんが、

波の変位を求めなさい。
と言われた時に、

変位って何ですか?
とはならないようにしてください。
それでは続けて、波長と振幅について説明していきます。
波長について

波長という長さは、色んな所に書くことができます。
一般に、こういうところを波長と言います。
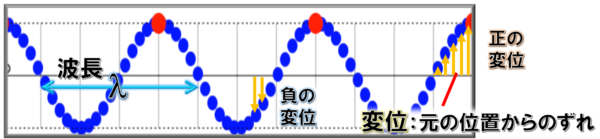
上図で示したところであったり、「山から山までの距離のこと」を波長と言います。
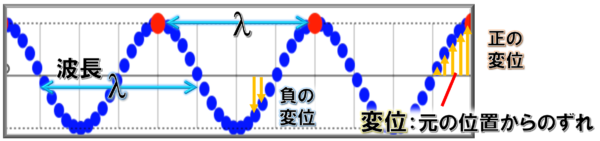

山から山より、ちょっとずらした所も1波長の長さに等しいので、それを波長と言っても構いません。
言ってみれば、これを波1個と数えているわけです。

これが1個ではありません。
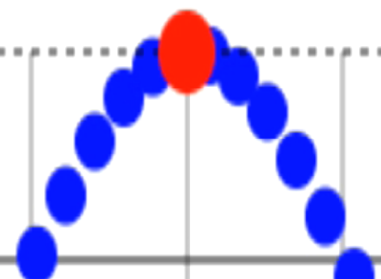

同じところから同じところ、同じ状態になるところまで、そこまでの距離の事を「波長」と言います。

一般に波長という時には、ほとんどの教科書がこういう風に書いてありますが、別に「山から山までが1波長分」としても構いません。
(波を1個2個と数える時には、これを波1個を数えることが多いです。)
次に振幅です。
振幅について
振幅とは、
どれくらいの幅で揺れてますか?
と言っているわけです。

したがって、振幅というのはここなんです。

振れている幅はこっからここまでじゃないか?
という人がいます。
確かにそうとも解釈も出来ます。

しかし、物理では振れ幅というのは、「もともとロープがあったところから最大でどこまで行きましたか?」という幅に統一されています。
ただ振幅については変位と違い、負になることはありません。
だから、振れ幅の大きさで答えます。

言い換えると「最大変位の絶対値。」であるとも言えます。
したがって、「最大変位の大きさ」という風に考えてください。

これらは用語の説明ですから覚えてください。
一般に波長や振幅はλとかAで表わしますから、λって言われた時には、

波長のことだな。
という風に考えられるようになってください。
それでは、続いて行きます。
波の「周期」と「速さ」について
先ほどの図は、ある瞬間にこうだったという図でしたが、ロープが常にこういう形をしているわけではありません。

こういう形だったものが、どんどんどんどん横へと、ず~っとずれていくわけです。

その様子を表すための量が必要になってきます。

波というのは、伝わる時に「それなりの速さ」を持って伝わっていくわけです。
波動とは、伝わることだと説明しました。
つまり、動きがあるわけです。

それでは、その動きとか波の速さは、一体どうしたら書けるのでしょうか…??
3.波の伝わる速さ
そこで3番目として、波の伝わる速さについて考えていきます。

「波の伝わる速さ」としましたが、これは「波の速さ」といっても構いません。
ただ、ここで気をつけて欲しいことがあります。

波の速さを求めなさい!
って言われたら、

それは波が伝わっていく速さであって、決して動かしている波源の手の速さではありません。

ロープを動かしている手の速さのことを言ってるんじゃなくて、波の形がすっと伝わっていく、この速さのことを言います。

ですから、今は波の伝わる速さと丁寧に言いましたが、波の速さって言われた時も、これと同じことですから、気を付けてください。
一般に等速で物が動くとき、進んだ距離というのは、速さ×時間、つまり、進んだ距離は速さ×時間という風に書くことができます。
そこで、こんな図を使っていきます。

今、ここで波を起こしているとします。
波を起こし始めて、波の先頭が今ここに来たとします。
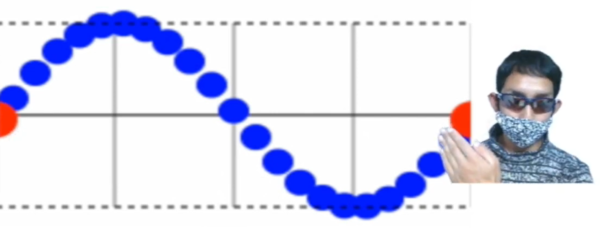
現時点で波の先頭はここです。
ところが、これがどんどんどんどん速さv [m/s]で、右向きに伝わっていきます。
【参考】[m/s](メートル毎秒):1秒間に〇〇メートル進む速さの単位

そして、とうとう波の先頭がここまで来たとします。
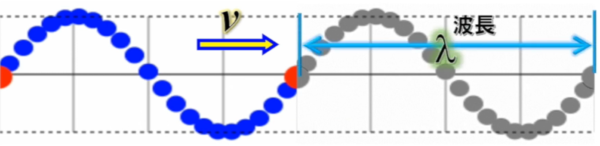
ちょうど波の先頭が1波長分進んだとします。

この波の先頭というのはvという速さで伝わっています。
波の先頭が進んだ距離が1波長に等しいんです。1秒間当たりv[m]の速さで進んでいます。

では、この波の先頭がここへ来るまでに要する時間は一体いくらなのか?
これについて考えてみます。
そうすると、それはちょうど波を1個作るための時間だということになります。
ここで、ちょっと考えて見て下さい。

ちょうど波を1個作るために要する時間というのは、
手の動きを見ればいいということですか…??
ロープを手でもって上下に1回往復させると、波が1個作れます。


つまり、この波のちょうど1周期分です。
行って帰って来るまでの時間で波を1個を作ることができます。
ということは、所要時間は振動の周期に等しいということになります。

ここで振動の周期、つまり波1個分進むのに要した時間を周期と呼び、Tで表現します。
そうすると、周期Tの間に進んだ距離がλ、速さはvです。

だから、等速で伝わるという条件であれば簡単に式が作れます。
図より、進んだ距離は、λです。進んだ距離は速さ掛ける時間に等しい。
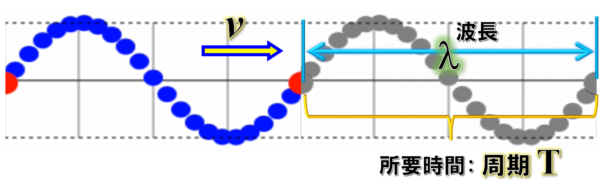
つまり、こうなります。
![]()
覚えるというほどのものではありませんが、これは非常に大切な式です。

言ってみれば、これはλイコールと書かれてますから、波長λの定義と言ってもいいでしょう。
1周期の間に進んだ距離、それはλに等しい。
という日本語訳ができます。

簡単に言うならば、進んだ距離は速さをかける時間で求まります。
「ただ、その時間がたまたま1周期分だから、その進んだ距離は、たまたま1波長になってますよね。」っていう考え方ですから、こういう風にλ=vTとなるわけです。

λイコールvT、λイコールvTと呪文のように覚えないでください。
物理の式というのは、和訳ができないと、いつどういう式を使っていいかがわからなくなってしまいます。

ですから、ただ単に公式を覚えて、どうのこうのじゃなくて、「λ=vTというのが一体どんな式なのか!?」ということが、常に和訳できるようになっていなければいけません。
重要事項の確認/関連記事へのリンク
これで波動現象について基本的な説明は、ほとんど終わりました。
このように振動してるもの、それが伝わるという現象が波です。
今回の解説の中できちんと押さえておいてほしいポイントを下のスライドにまとめました。
(答えは次のスライドの右下の赤字で示してあります。)
文字化けして上手く表示されない場合は、こちらの動画を利用してください。

物理の学習ではきちんと用語や定義を押さえていかないと、内容理解が追いつかなくなってしまいます。
この記事の内容を始めて学習した方や、先々の内容があまり理解できないと感じる方は、一度基礎に戻って、専門用語や数式の内容を確認してください。