はじめに
今回から具体的な波ということで、弦と気柱の固有振動について進めていきます。
前回は音の性質ということで、音波が伝わる仕組みだったり、伝わる速さについて見ていきました。
ここでは、その続きとして、弦と気柱というものを扱っていきます。
弦と気柱の固有振動について

弦の方は問題ないと思うんですが、気柱っていうのはちょっとわかりづらいかもしれないです。
皆さんの中には例えば吹奏楽部とか、軽音楽部に入っていて、楽器に詳しい人もいるかと思いますけども、例えば、弦楽器といえばギターとかです。

そういうものが浮かんでくるかと思うんですが、そこまで難しいことを考えなくても、例えば…
一本、ちょっと細い糸みたいなものがあったとします。

パンって真ん中を弾くと「ブゥ~ン」ってなりますねぇ。
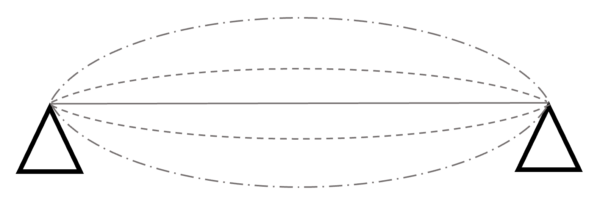

あの話をしようって訳です。

気柱…。

これは、難しいです。
でも、皆さんの中にもやったことがある人もいると思います。

最近はだいぶ少なくなりましたけど…
瓶に入っているジュースを飲んでる時に、途中で唇をつけて「フゥ~」ってうまく吹くと
「ボぉ~」って大きな音が出ます。

「そういうような話をこれからやりましょう」っていう訳です。

それがいわゆる弦と気柱の固有振動という
難しい題名になってしまうんです。
いつも言っているように、難しい用語で自分をごまかさないで、実際に、それが生活の中に行くと、どんなことを言っているのかということが説明できなければ、それは物理を学んだことにはなりません。

ですから、難しい言葉は使いますが、正しく理解してください。
固有振動について
では、そろそろ弦と気柱の固有振動の本題に移っていきますが…

固有振動って一体何でしょう…??

こういったところから、きちんと見て行かないといけません。
これまでに波の表し方ということで、定在波について学習しました。

定在波とは、簡単に言えば同じ波が逆向きに進み、重なり合ってできる合成波のことでした。
2つの波が重なるんです。

そうすると、合成波は、どう見えるか…?

止まって見えるんです。

これが定在波です。
定まって在る波です。

動いてるように見えないということです。
定在波というのは、それだけのことなんです。

実際には2つの波が進んでいるんです。
だけど、止まって見えると言ってるんです。
それが一体何を意味しているのかっていうことです。

それでは、今度はこんなことやってみます。
両端を固定した一本の糸がピンと張られています。

そして、パ~ンと弾いてみるんです。
例えば、弦の真ん中のあたりをバァ~んとはじいて振動を与えます。
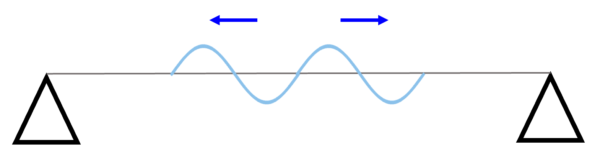
そうすると、波が、糸を伝って進んでいきます。

端っこは固定されています。
だから、ここにあたって、波が跳ね返ります。
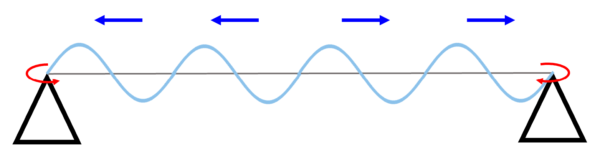
そして、2つの波が重なります。

これで定在波ができるんです。

今度は、実際に装置を使って確認してみます。
もともと弦が横にピンと張られているんです。

そして、弦を振動させていきます。
徐々に振動数を上げていくと、定在波が観察できます。


両端は固定されているので動かない一方、真ん中は大きく振動しています。
さらに振動数を上げていくと、さっきの2倍の振動数のところで、再び定在波が観察できます。


しかし、さっきと波形が異なります。
真ん中はほとんど動いていません。

そして、節と節の間で大きく振動しています。


そして、さらに振動数を上げていくと、最初の振動数より約3倍のところで、定在波が観察できます。


今度の定在波は、腹の数が3つになっています。

腹の位置では、凄く激しく動いてるんです。

確かに節と腹が交互に並んでいます。
これが定在波と呼ばれるもので、弦のように両端を固定されたものを弾いて
波を与えた時に、

行く波と戻ってくる波…

つまり、同じ波だけど互いに進行方向が逆向きの波が重なる。
この時に定在波ってものが出来上がって、このようになるということです。
それから、定在波のところで学習した内容を思い出してください。
この部分の波形が1波長だとすると…
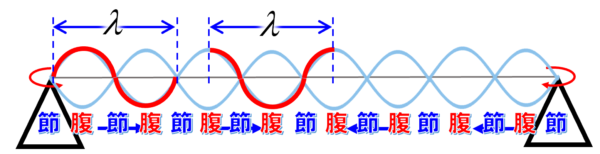

確かに、節から節まで、もしくは腹から腹までの区間が1波長の半分に相当しているということも分かってもらえると思います。
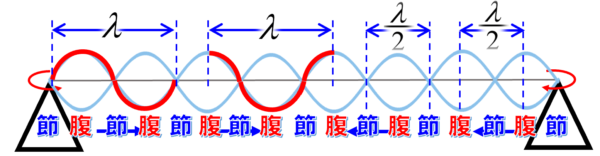
このように、1本のロープを上下に振動させたときに波形が進んでいく波の他に、弦のように両端が固定されたものを弾くと、定在波ができる。

そういう波をこれから扱っていきます。
ギターなど、いわゆる弦楽器はこうして音を出しているわけです。

このような振動をこれから考えていくんですが、タイトルに固有振動と書いてあります。

固有というのは、
「何かに固有のもの」
という意味です。
ここでは、弦に固有のもの、気柱に固有のものという意味になります。

弦とか気柱というのは特定の…「弦なら弦」、「気柱なら気柱」に固有の定在波しか作ることができないんです。
弦の固有振動(両端が固定端)
さっきの装置に戻りますが、弦は両端が固定されているため、両端は絶対に節になります。
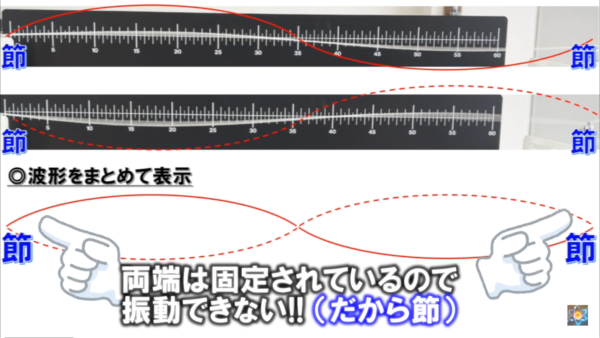
だから、ちょうど端と端がちょうど節になるような、特定の定在波しか作ることができないんです。

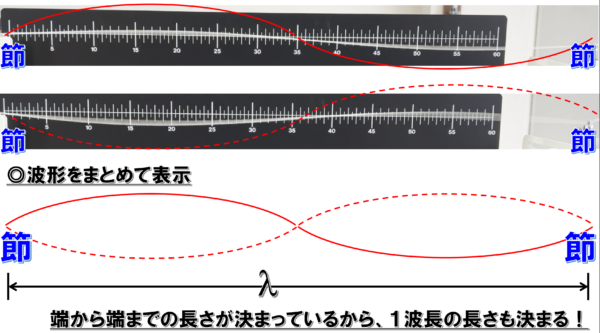
特定の定在波しか作れないということは…

1波長の長さも定まってしまいます。
それから、弦を伝わる波の速さは、弦を引っ張る力と弦の材質によって決まることがわかっています。

ということは、同じ弦を利用している限り、速さも一定です。

したがって、波の基本式v=fλより、vもλも特定の値だから、fも特定の値に定まります。
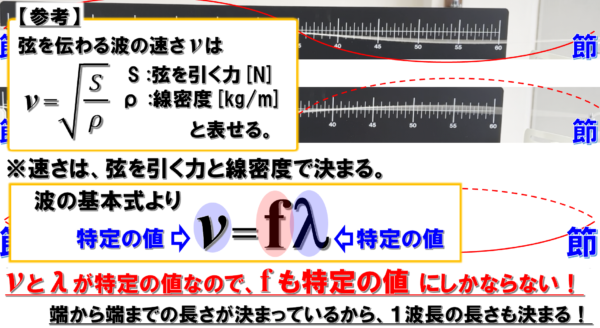
「振動数」が、弦によって固有の値となるから弦の固有振動という訳です。

このように、定在波ができる時の特定の振動数のことを固有振動数と言います。
弦を振動させる時は、両端が節になるような固有振動数を与えてやると定在波ができるというわけです。
基本振動、2倍振動、3倍振動

そうすると、次は、どのような定在波ができるかということが気になってくるところです。
固有の振動数を与えないと定在波は出来ないので、特定のものしかありませんが、それでも定在波はたくさんあります。

それ全部挙げていくときりがないので、最も波長の大きいものから、順番に考えていきます。
波として最も大きいものっていうのは、節と節の間隔が最も大きくなれば良いわけですから、
次のような定在波が波長が最も大きいパターンになります。
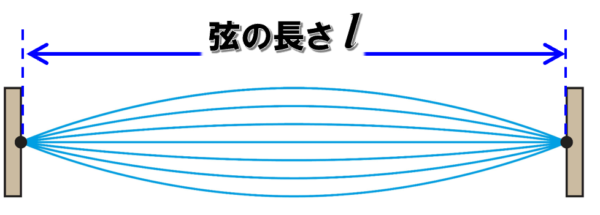
今、この弦の長さをlとします。
そうすると、節と節の間隔は1波長の半分だから
lは、λ/2ということになります。

1波長というのは、もう1個右側にあるような長さだと思ってください。
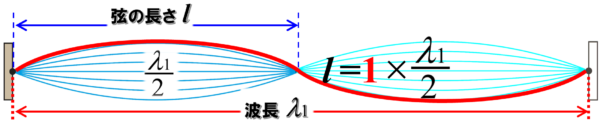

ただ、ここで注意してほしいことは、
lイコール2分のλが1個って書くんです。
ここの赤い文字で書かれた1を忘れないようにしてください。

この1がとても大切です。
その重要性を確認するために、次に波長の大きい定在波を見ていきます。
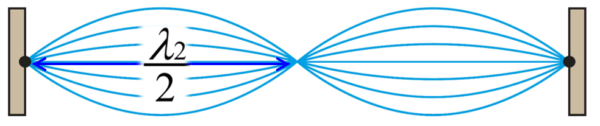
節と節の間隔が2分のλです。そして、端から端までがlです。

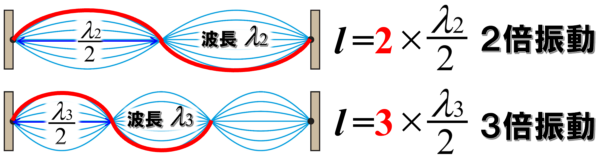
それでは、この場合は、lイコール2分のλが2個です。


lは、λ/2が2つ分です。
そして、次に波長が大きいものを考えていきます。

節から節までが2分のλ。
端から端までがl

じゃあlイコール…?

2分のλが1、2,3個…

2分のλが3個…
となります。

一番上の定在波は、1番波長の大きいものを扱ってるから、λ/2が1個入ってますよって言うんです。
真ん中は、λ/2が2個。そして、一番下は3個。
つまり、端っこが止められているということは、
どんな定在波ができるにしても、この芋型の波形を1つの単位として、

この形、この形という風な波形になってないといけないわけです。


弦の固有振動というのは、芋型の波形が何個入ってるかっていう話なんです。
だから、波長が一番大きい場合が、一番少ないんです。
だから1個です。

でも、2個入ることもできます。

3個入ることもできます、4個入ることだってできます。


でも、これが1個2個3個入る時でないとダメです。

1.5個とか1.3個は、ダメですよって言ってるんです。


だから、この1という数字が、すごく大事なんです。
この赤い文字で書かれた1は、芋型の波形が1つ分しか入らないということなんです。

これを基本振動といいます。
だから、2個入る時は2倍振動、3個入る時は3倍振動…、
一般には、mを用いてm倍振動といいます。
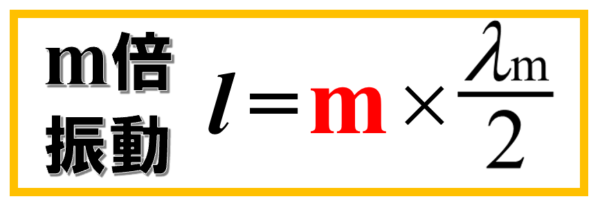

だから、mが例えば5だったら5倍振動です。
こうしておくと、mの数字を入れ替えるだけで、すべての定在波の波長の関係がわかります。

なかなか良く出来ています。

一番基本になるものをポコッと一つ書いておいて、
それが何個あるかによって決まるんです。
そうすると、これは2倍振動、これは3倍振動なんだっていうことがすぐにわかります。

それさえ分かってしまえば、後は簡単です。
たとえば先ほど、弦を伝わる波の速さは、弦を引っ張る力と弦の材質によって決まると言いました。

だからvさえわかっていれば、波の基本式 v=fλ の式を使えば、fがわかります。
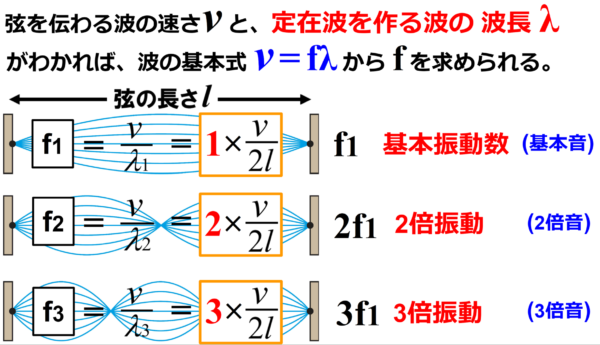
もしも弦をはじく振動数がわかっていれば、何倍振動かを見てやれば、λがわかるわけですから、
vを求めることだってできる。

こうやって用語をただ単に1つずつ覚えていくんじゃなくて、基本振動っていう大元があることをきちんと押さえていく。
そして今度は、その基本振動が何個あるかということを考えるのが、倍振動と呼ばれるものだと、そんな捉え方ができるようになります。
これで、両端を固定した場合の固有振動については、一通りの説明が終わりました。
次回は、両端が固定していない場合を考えていきます。














