はじめに
今回は、波の表し方の後半ということで、定在波の形成と自由端、固定端による反射について解説します。
次の授業で、音に代表される具体的な波を取り扱っていきます。

その際、これから学習する定在波と波の反射については、とても大切になってくるので、1つ1つ丁寧に進めていきます。
そこで、本題に入る前に1つ、波の性質について大切なことを確認しておきます。

それが波の重ね合わせの原理です。
重ね合わせの原理
波は、物体とは異なり特殊な振る舞いをします。

物体同士が接触すると反発し、運動の向きが変わったり物体が変形したりしますが、波は異なります。
波同士が接近すると衝突して反発するのではなく、互いに重なり合って何事もなかったかのように通り抜けます。
【参考動画】
これを波の独立性といいます。

波が重なり合う時、その場所の媒質は、それぞれの波の変位が足し合わされたように変化します。



例えば、山同士が重なり合うと、重なった部分の変位は大きくなります。

一方、山と谷が重なると、互いの変位を打ち消すように振舞います。


このような現象を波の重ね合わせの原理といい、重ね合わせによって生じた波を合成波と呼びます。

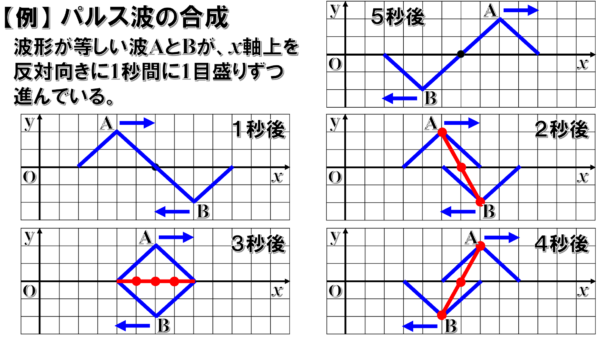
パルス波の合成

合成波は、私たちが実際に目で見る波であり、実際には2つ以上の波が重なり合って生じる波です。
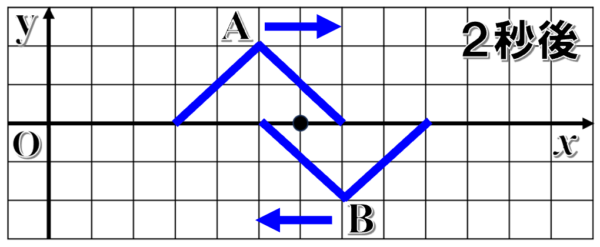
例えば、図のように波形が等しいパルス波AとBが、x軸上を反対向きに1秒間に1目盛りずつ進む場合…

それぞれのパルス波を1秒毎に進めていくと、1秒後に互いに重なり始めます。

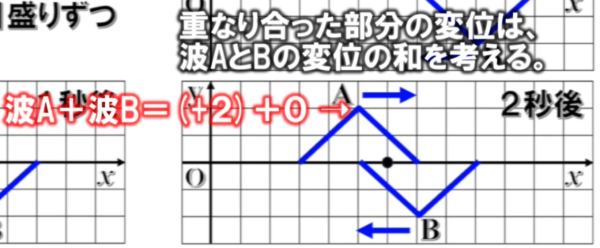
そして、2秒後には、それぞれの波は図の位置に到達するので、重なり合った場所のマス目の部分の変位を確認してみます。
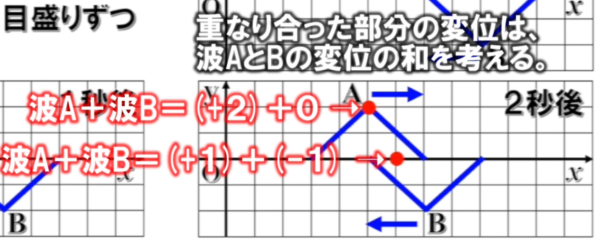
左側から順番に y=y1+y2を計算すると、2+0で2
中央が、1ー1で0
右側が0ー2でマイナス2となります。
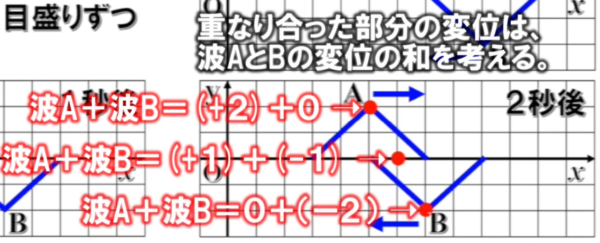
赤い点を結んだ線が合成波の波形になります。

したがって、合成波は図の赤線のようになります。
同じように3秒後、4秒後、5秒後、6秒後の合成波を確認すると、図のようになります。

イヤホンなどに搭載されているノイズキャンセリング機能は、音波の波動性を利用して外部の不要なノイズを減少させる技術で、波の重ね合わせの原理を活用しています。
ノイズとして認識された音波に対し、逆位相の波を送り出して互いの振動を打ち消すことで、静かな環境を実現しています。

定在波について
それでは本題の定在波に移っていきます。

定在波とは、波長とか振幅が等しい2つの波が、お互いに逆向きに同じ速さで進み重なり合った時にできる合成波です。
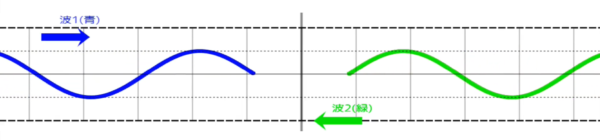

反対向きに同じ速さで進む、波長と振幅の等しい正弦波が重なってできる合成波は、どちらにも進んでいないように見えます。
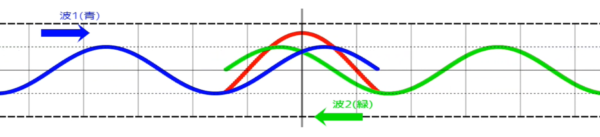
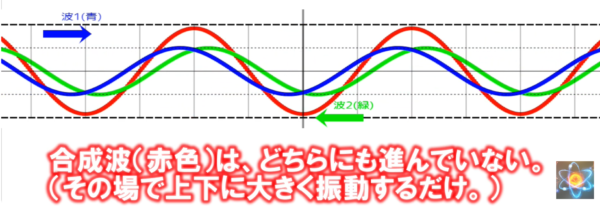
このような波を「定まって在る波」ということで定在波といいます。
ちなみに、今まで扱ってきた媒質の振動が伝わって見える波を進行波といいます。

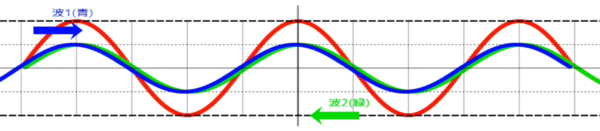
定在波の波形を観察すると、まったく振動しない「節」と呼ばれる所と大きく振動する「腹」と呼ばれる所が交互に並んでいることが確認できます。
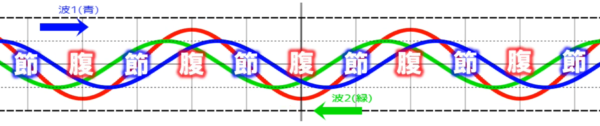
そして、定在波の波形をしばらく観察してみると、腹の位置で振幅は、もとの波の2倍。
振動の周期は、もとの波と同じでTとなります。
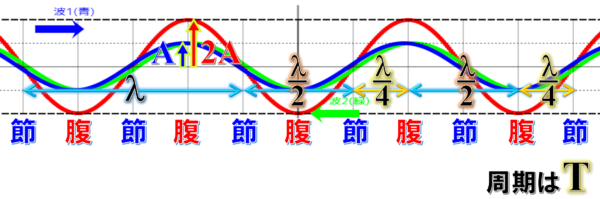
つまり、もとの場所から行って帰ってくるまでの時間がTです。

だから、山であれば、谷まで行って再び山に戻ってくるまで。
谷であれば、山まで行って再び谷に戻ってくるまでの時間がTです。
腹と節の間隔は、もとの波の4分の1波長、腹同士の間隔や節同士の間隔は、もとの波の2分の1になっていることが確認できます。
定在波の形成
例えば、図のようなx軸上を反対向きに同じ速さで進む正弦波A、Bが重なり合う場合

1秒ずつ波を進めて波形を確認していくと、図の赤線で示すような合成波が観察できます。
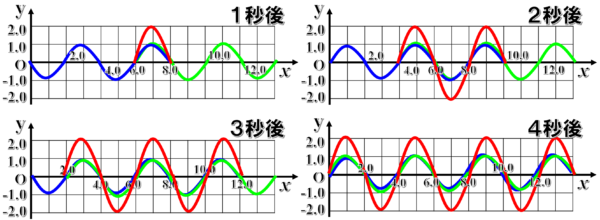
この合成波の波形をまとめてみると、定在波を形成していることが確認できます。


この時、隣合う節と節の間隔は、2.0m、節と腹の間隔は1.0mです。もとの正弦波の波長が4.0mなので、それぞれ2分の1波長、4分の1波長の関係を満たしていることがわかります。
また、振幅は2.0mでもとの波の2倍、周期は上下に1回振動する時間なので、腹の位置の振動を見てみると、1秒後には、反対側に移動して、2秒後にもとの位置に戻ってくることが確認できるので、腹の位置の振動の周期は2.0秒です。
もとの波の周期は、波の基本式v=fλより、速さが2.0m/s, λが4.0mより、f=0.50Hz
f=1/Tの関係より、T=2.0s
したがって、元の波と合成波(定在波)の周期は同じであることがわかります。














