目次
はじめに
前回の講義で仕事とエネルギーというものを勉強してきました。
これについて、少し復習をしておきます。
数式は、後からついてくるものです。
今は現象をしっかりと捉えなければいけません。
□動画による解説はこちら↓↓↓
仕事とエネルギーについて(復習)
仕事という現象です。

仕事というのは力を加え、どれくらいの距離、物体を移動させたかということによって評価されるものでした。
ですから力が一定であるならば、一定の力Fと、それに距離xを掛け算する。それによって仕事というものが評価されるということでした。

一方、エネルギーというのは、「仕事をする能力という考え方をすれば良い。」ということでした。
それに関して式としては1/2mv2だとか、mghだとか、1/2kx2だとか、色々あったわけですが…

要は何なのかっていうと、所詮僕たちが扱っているのは物体です。勝手に能力が増えたり減ったりはしません。
例えば運動能力が増えているということがあるならば、それは誰かが何かしたんです。

力学でいう誰かがっていうのは力のことでした。
エネルギーを考える時に何かをしたっていうのは、その力でもって距離xだけ移動させたとか、そういうことになるわけです。

いわゆる仕事をしたせいである。
だから、

運動エネルギーが変化しましたよ。
増加しましたよ。
っていう時は、

あっ、誰か仕事したな!
っていうことが分かるわけです。

それから、元々位置エネルギーというものを持っていないものについて、ボールを例に考えました。
ボールを持ち上げる

手を離すと落ちる


テーブルの上に置いてあるボールと、そこから持ち上げたのでは、落下能力という意味では違いがある。

その落下能力は、誰のせいで身につけたんだ。

それは私のせいです。

私がmgに逆らってhだけ持ち上げるということをしたためです。
というような話をしました。

こうやって、まずは仕事ということを勉強し、
そしてエネルギーというものを勉強する…
その中でエネルギーと仕事の関係というものを見出すことができたわけです。

そこで今回は仕事の議論ももちろんするんですが、エネルギーを中心に進めていきます。
エネルギーの保存則について
エネルギーを中心にっていうのはどういうことかって言うと、実はエネルギーというのは保存則が成り立ちます。

保存則というのは、ある状態でのエネルギーと別のある状態でのエネルギー…
それぞれのトータルは保存する。
変わらないという意味です。

そのことについて、間に「仕事」ということを介在させて説明をしていきます。
もちろん、これも全てに対して成り立つものですから、例を挙げて説明していきます。
力学的エネルギーについて
そこで今から、力学的エネルギー保存則について考えていきます。

力学的エネルギー保存則というものを、これから説明をしていく訳ですが、力学的エネルギーっていうのは、一体何かということをまず説明しておかないといけません。
力学的エネルギーというのは、運動エネルギーと位置エネルギーの和
つまり全体のことを言います。

だから皆さんが、知っているもので言うならば、運動エネルギーと重力による位置エネルギーと弾性力による位置エネルギーのトータルのことです。
そのことを力学的エネルギーという風に呼んでいます。

一般に運動エネルギーは、カイネティックエナジーといって記号はKを用います。


それから位置エネルギー、ポテンシャルエネルギーとも言うんですが、
これは一般に記号はUを用いることが多いようです。
ここでもUという文字を用います。
そして、いずれも単位は仕事の単位と同様に大文字でJ、
ジュールという単位を用います。

言ってしまえばエネルギーは、仕事との互換性があります。仕事をしたからエネルギーに変化があったという考え方をしますから、単位としては同じものを使います。
教科書にしてもそう参考書にしてもそうなんですが、こういうKとかUとかいう記号が突然出てきます。それに合わせて、また単位がこうやって出てきます。

だから、頭の中がごちゃごちゃになりそうになるんです。
ですから時々…
こういうのは記号でこう表します。
ただ単位はこうですよ。
っていう風にまとめておくと、何のことだったっけっていうのも、すぐに確認出来るようになります。

ただ、一般によく用いられる記号というのは、
知っておいた方がいいと思います。
エネルギー保存則について

それでは準備が整ったので、本題のエネルギーの保存則を見ていきます。
これから運動エネルギーと位置エネルギーのトータルが変わらないということをやっていく訳です。

私たちは今、位置エネルギーについては2つ知っています。
ただ、今回の例では、簡単な方で進めていきます。
ですから、重力による位置エネルギーの方を考えていきながら運動エネルギーとのトータルがどこの場所に行っても変わらないということが本当に成り立つのかどうかいうことを実際にやってみたいと思います。

少し余談になりますが、力学的エネルギー保存則って言ってますが、実際には、どんどんと勉強を進めていくと、この力学的というところにカッコがつき始めてきます。
そのカッコがつき始めるっていうのは、別に力学だけに縛られる必要はないということを意味します。

皆さんも、生活の中でそういうことやってるんです。
例えば、寒い時にこういうことをします。


「寒いねぇっ」て何やってるんですか?
こうやると手が暖かくなります。

暖かくなるっていうことは、この時、熱エネルギーができます。
エネルギーは勝手に生まれてきません。だから私は仕事をしています。
手と手の間の摩擦に逆らって、動かして距離を稼いでいます。

熱エネルギーは、やはり仕事から生まれてくるんです。だから本当は、最終的には力学的エネルギー保存則じゃないんです。
エネルギー保存則です。力学だけじゃなくて、熱や電磁気も含めたエネルギー保存則です。

しかし、物事には順番っていうものがあります。
ですから、まずは私たちが勉強した力学的エネルギーの範囲で、考えていきましょうということです。

皆さんも物理とかに興味ある人は、アインシュタインとかホーキング。
こういう人たちによって宇宙論というものが展開されたのは、ご存じだと思います。


そして今は、超ひも理論とか色々出ていますが、その中に、ビッグバン理論っていうのがあって、
「宇宙の始まりはきっとこうであったに違いない。」という…

こういうことは、科学雑誌なんかで見たことがある人もいると思うんですが…
とは言っても、それを実際には見に行けません。
それはそうです。「宇宙のはじまりを見にいきましょう。」って言っても、そんなものは見に行けないです。

じゃあ一体、何でこうしてまるで見てきたかのように、ビッグバンの時のイメージが描かれているの!?

なぜ、そんなことができるのかっていうと、
実はエネルギー保存則を使って計算がしてあるんです。
現在の宇宙の状態っていうのは、いろんな方法を使うと測定できるんです。
例えば、波の分野で勉強する干渉とかドップラー効果とか…
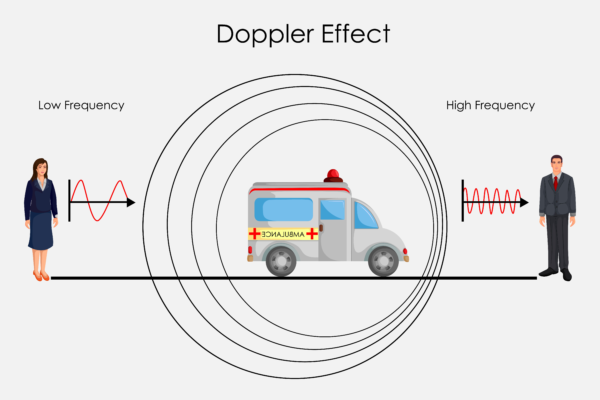
そういうものを利用しながら、星々がどんな動きをしてるかっていうことを観測して全部計算することができるんです。

ということは、今現在の宇宙のエネルギーは計算できるんですねぇ・・・。
でも、エネルギーっていうのはね、勝手に増えたり減ったりしないんです。最初と同じなんです。じゃあ、そのエネルギーが一箇所に集まったら、「一体どれぐらいのエネルギーになるか。」っていうことが分かるわけなんです。

そうやって、保存しているっていうことをうまく利用して、現在の状態を見ることで、「昔がどうだったはずである!」って言えるようになってくるわけです。

それなら、エネルギー保存則は、とても大切です。
ということで、その大元になることを勉強していきます。
力学的エネルギー保存則
落体の運動による解説(図による理解)
さっきも言ったように、熱エネルギーとかもいろいろ入ってきますが、まだ、それはちょっと置いといてビッグバンの理論とかは大変ですから皆さんがよく知っている落体の運動できいます。

これは等加速度運動です。
それでは具体的な例について考えていきます。

ある高さのところにある物体を考えます。
ここから物体を初速v0で投げ下ろすことを考えます。

そうしたときに「この辺に来た時に物体は、vという速さになっていた。」とします。
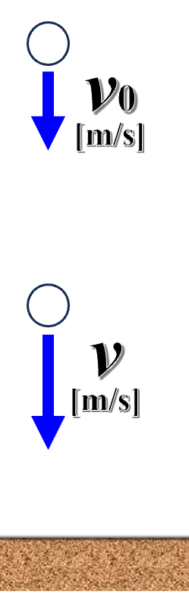
これも皆さんは、見方が分かってくると思うんです。

下向きに重力加速度があるからだなあ…

そういう考え方でも良いんですが、もう既にエネルギーの勉強しましたから、これは1/2mv02だけど、こっちは、1/2mv2。

そして、こっちのほうが多いということはすぐ分かると思います。

じゃあ、誰かが何かしたんだ。

そうです。「重力がこれだけ引きずり下ろしたからです。」っていう考え方できます。
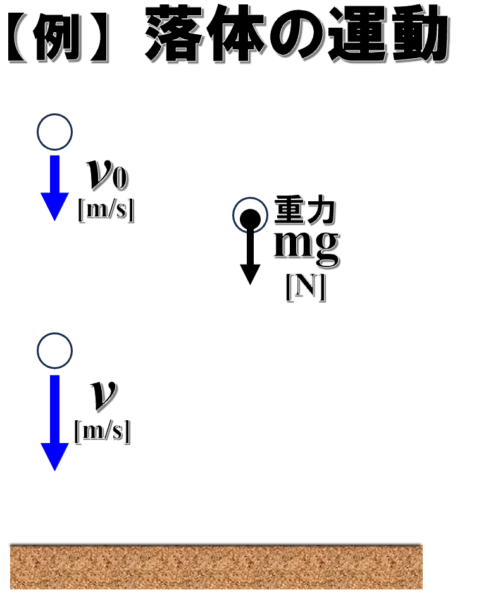
それで、基準点を決めたいので、この辺を地面とします。

こういう設定をちゃんと頭入れておいてください。
そして、地面からhゼロの高さから落としたとします。
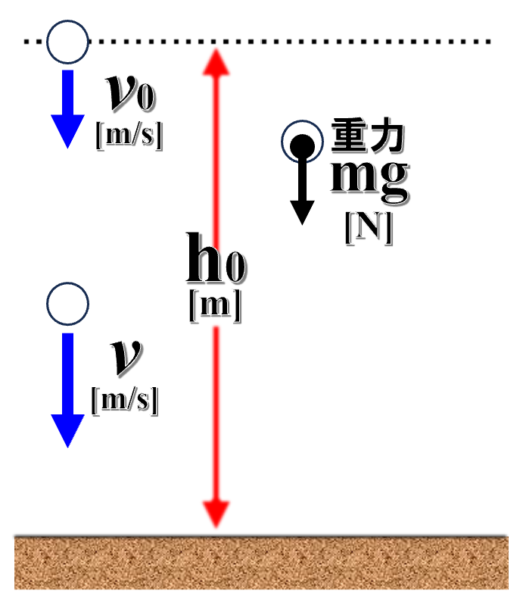

どうしてこういう事をやるの?

「力がどのぐらいの距離」働いたかということが、ものすごく大事なんです。だから距離を設定したんです。
等加速度運動で落体の運動だったら時間についても気になるところですが、今は、とりあえず時間は考えないことにします。(時間についてはまた別の機会に見ていきます。)
それから、vという速さになっている時、そこの高さをhと置いてみます。
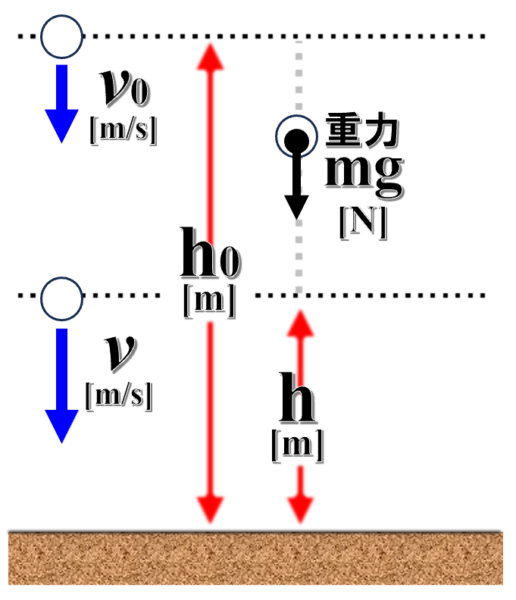
そのとき、ここからここへ来るとき、一体誰が何をしたかを考えます。
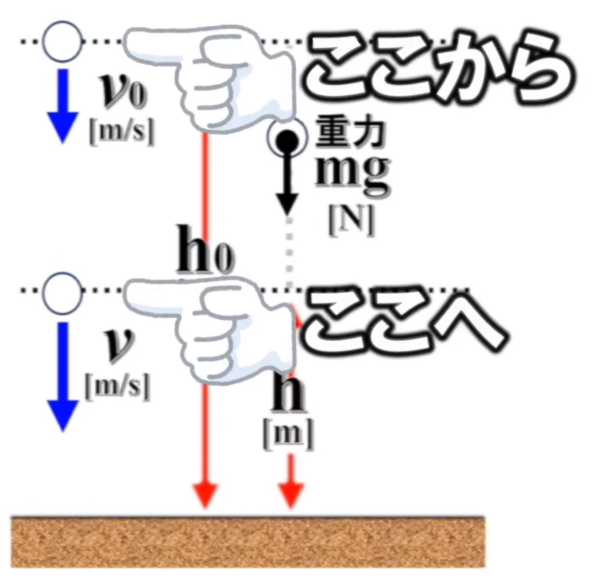

それはもちろん、接触力は働いてないので重力です。
重力が物体をここからここまで引きずり下ろしてきた訳です。
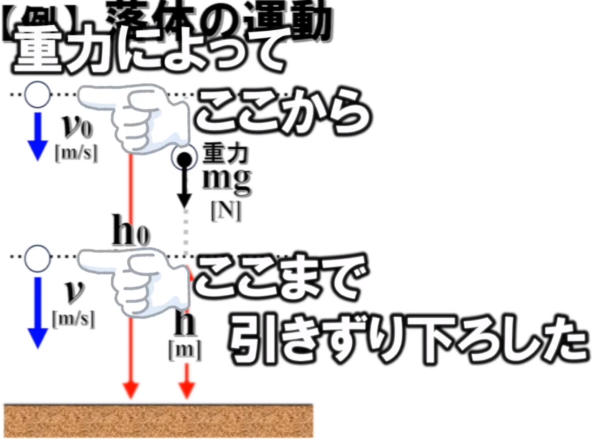
ですから、ここからここの間で、mgという力がh0ーhだけ働いたことになります。
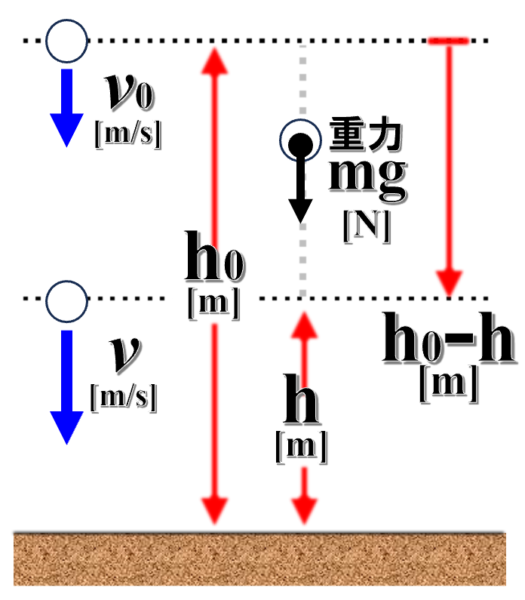
ここまでの説明で、この図の意味を分かってもらいました。
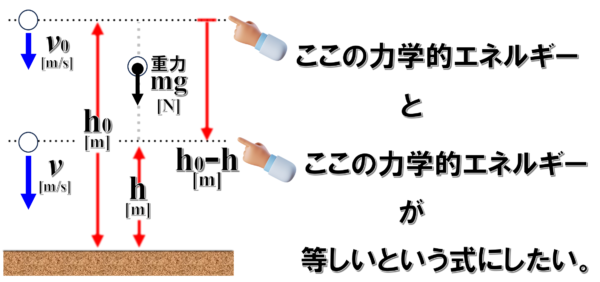
このとき、今回の目的が何かというと、こんなことをやろうっていう訳です。
ここでの力学的エネルギーとここでの力学的エネルギーが同じだってやりたいです。
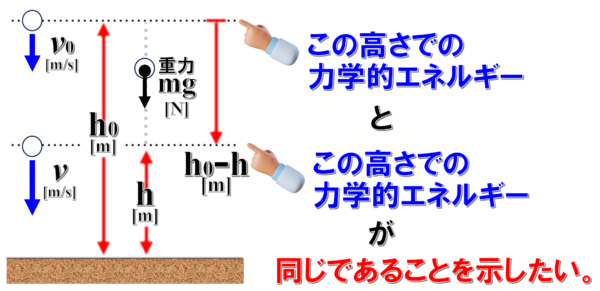

なんか…「え~っ」て感じがしますね。

こっちのほうがでかいんじゃないの!?

しかし、よ~く考えてみてください。
エネルギーっていうのは、運動だけでは決まりません。
もう1回いきます。力学的エネルギーっていうのは、運動エネルギーだけじゃないんです。位置エネルギーもあるんです。
だから、運動エネルギーがでかくなったかもしれません。

でも、運動エネルギーがでかくなったっていうことは、もしトータルが同じならば、この位置エネルギーは減ってるはずです。
もう1回いきます。
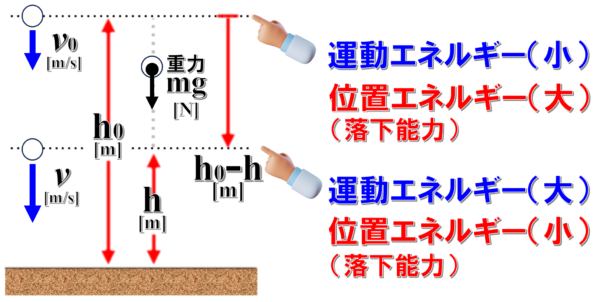
上の方の運動エネルギーは小さいです。下の方は大きいです。
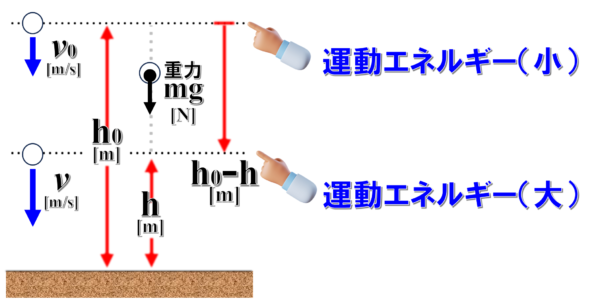
だけど、その時は、この場所とこの場所で落下能力を比べたら…

上の方の物体は、こんなにも落ちることができるけど、下の方だと、もうこれだけしか落下できません。
運動エネルギーが上がったかもしれないけど、位置エネルギーは減ってます。
これから式をどんどん作っていくんですが、その前に、まずはこうして感覚的に捉えておかないといけません。

運動エネルギーが増えているっていうことは、これは誰が見ても分かることです。だから下の方が大きいのかなという感じがするんです。

ところが実はそうじゃない。落下能力まで合わせて加味すると、上の方が落下能力が大きいだろう。

じゃあ、下の方が落下能力が小さいだろうということがわかる。

それなら、トータルとして、「もしかしたら変わってないかもしれないね。」というようなことが分かってくる。
落体の運動による解説(数式による理解)
それでは、今度は数式で考えていきます。

まずmgという力でh0-hだけ。
すなわち、ここです。
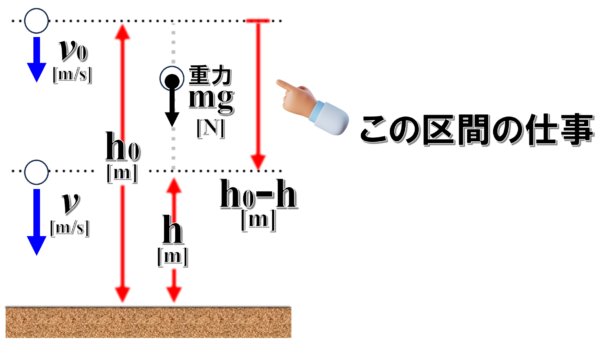
これだけ仕事をしました。

誰が仕事をしたの?

もちろん重力が仕事をしました。
重力mgが距離h0-hだけ物体を移動させた。


雑な言葉を使えば、mgという力で物体を引きずり下ろした。
そして、この現象に対して、重力のした仕事を考えます。
W=力×移動距離。これだけです。

エネルギーと仕事の関係より、運動エネルギーが変化する。

それは誰のせいですか?

誰かが仕事したんです!
運動エネルギーは、最終的に1/2mv2になりました。
最初は1/2mv02でした。
つまり、1/2mv02だったものが、現在1/2mv2になっています。

それは誰のせいですか。

それはmgがh0-hだけ働いたからです。

ということは、mg×(h0-h)

こうなるんです。

前回の授業の時、エネルギーと仕事の関係を考える時に一般にとかやって、こういう風な式があったのは覚えているでしょうか??

運動エネルギーの変化をもたらしたのは、力がこれだけの距離働いたからです。
元々、v2-v02=2ax という式から始まって
両辺にmをかけて
さらに両辺に2分の1をかけて
右辺のを仕事という行為に変えた訳です。


これより運動エネルギーの変化は、力に距離をかければいい。

今回も、力に距離を掛けたんです。
勘のいい人は、もうこの辺でわかるんじゃないでしょうか…??

この式には、引き算が入っていますが、引き算じゃダメなんです。
私たちは、保存則が欲しいんです。

これとこれの和(最初の力学的エネルギー)がこれとこれの和(最後の力学的エネルギー)に等しいっていうのが保存則です。
それなら引き算はまずいです。だから変形します。

こっちの場所での和と、こっちの場所での和が等しいという式に持って行きたいんです。

ですから、マイナスが付いてるものは全て移行します。
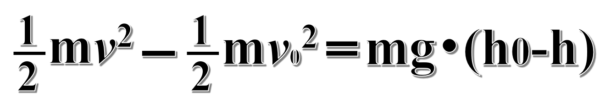
反対側に持っていきます。
右辺を展開するとマイナスmghだから、マイナスmghは左辺へ持っていきます。
1/2mv02は、右辺に持っていきます。
mgh0は、そのままです。
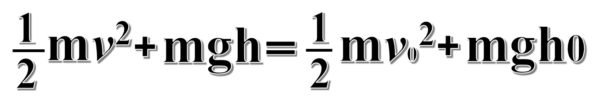
下の方での運動エネルギーと位置エネルギーの和は、上の方の運動エネルギーと最初の位置エネルギーの和に等しい。


最初の位置と現在の位置で(力学的)エネルギーが等しいという式になってます。
これがエネルギー保存則です。
こうやって、元々は重力mg×移動距離hという考え方だったのを位置エネルギーに持って行くと、それぞれ、現在の運動エネルギー、位置エネルギー、元々の運動エネルギー、位置エネルギーとやった時、
元々の運動エネルギーと位置エネルギーのトータルは、
現在の運動エネルギーと位置エネルギーのトータルに等しい。
すなわち、右辺が最初の力学的エネルギーの和。
左辺が現在の力学的エネルギーの和。
それが等しいというわけです。

良くできています。
こういうのを力学的エネルギー保存というふうに呼んでいます。
例題解説
それでは、ここで例題を解いておきます。
地上から10mの高さにある質量0.50kgの物体を自由落下させた。地面を基準水平面にとり、重力加速度の大きさを9.8m/s2とする。
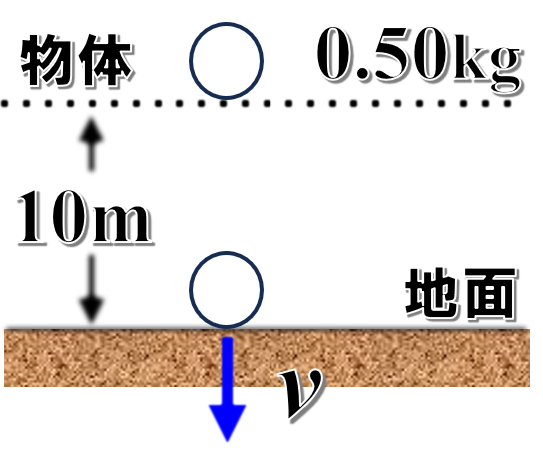
(1)自由落下させる直前の物体のもつ力学的エネルギーは何Jか。
自由落下させる直前ですから、自由落下させる直前の物体の速度をv0とすると、物体は静止しているのでv0は0です。
したがって、運動エネルギーは、1/2×0.50×0ですから、0 。
位置エネルギーは、mghですから、0.50×9.8×10=49[J]
したがって、力学的エネルギーは、0+49で49[J]なります。

(2)力学的エネルギー保存則を用いて、地面に達する直前の物体の速さv[m/s]を求めよ。
地面に達する直前は、基準水平面と同じ高さにあるので、重力による位置エネルギーは0です。
運動エネルギーは、1/2×0.50×v2 です。
したがって、自由落下させる直前と地面に達する直前の力学的エネルギー保存則を考えると、
0+0.50×9.8×10=1/2×0.50×v2+0 で、
これを計算するとv2は196となって、vは14m/sとなります。

それでは、今回の解説は以上となります。