目次
はじめに
今回は液体や気体から受ける力について解説します。

この力のことを水圧とか気圧と言ったりしますが、天気予報なんかで高気圧だとか低気圧だとかよく聞きます。


低気圧がやってくるというのは、1気圧に比べて高いか低いかということを言ってるだけで、結局何なのかということがよく分かりません。

そこで、まずは気圧や水圧の前に、
圧力について考えてみます。
圧力について
圧力というのは、後の漢字が力という字です。
それで、この棒を使って説明をすると、棒のこちら側は尖っていません。

↑棒の平らな方

↑棒のとがった方
一方のオレンジ色の方は尖っています。
それで、この棒の両端を手の平で、同じ力で押さえます。

例えば、10Nでぎゃっとおさえるとします。
そうすると、この平らな方…


こちらはそんなに痛くないんです。
しかし、このオレンジ色の方は尖っているから、こちらは痛いんです。


何が言いたいかって言うと…
今同じ力なんです。
同じ力なのにもかかわらず、こちらは大して痛くないけど、こちらは痛いんです。

↑こちらは大して痛くない

↑こちらは痛い

ということは、力だけで議論できない部分があるということです。
だから新しい物理量を考えていかないといけない。

それが圧力なんです。

「こちらは尖っていない。」「こちらは尖っている。」
っていうのは、何が違うのかってことを考えればいいわけです。
そうすると…
この先は、面積が小さいんです。

↑面積が小さい

↑面積が大きい
こっちは面積が大きいんです。

面積が大きな方は10Nを、広い面積で支えるから、大したことないんですが、面積が小さな方は、小さな面積に全部の10Nがかかってくるんです。
圧力の定義
ですから圧力というものをこういうふうに定義してみます。

単位面積当たりの力…

すなわち圧力Pというのは単位面積当たりの力。
もしくは、力というのは圧力かける面積と表現することも出来ます。

例えば私たちが考える圧力っていうのは、今かかっている力を面積で割ってくださいってことです。
そして、面積1m2当たりに1Nの力を垂直に加えた時の圧力を1パスカルと言います。

そうすると、同じ力でも、この面積が大きければ大きいほど圧力は小さくなります。面積が小さければ小さいほど圧力は大きくなります。
圧力の計算例

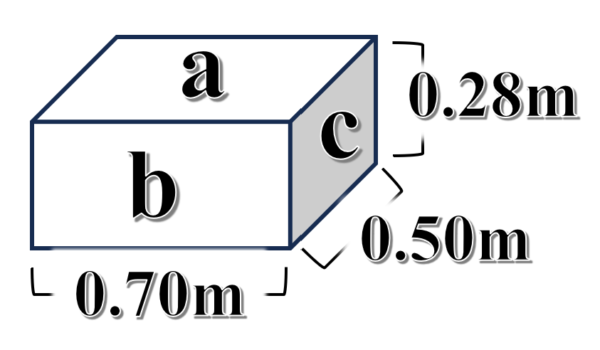
例えば、図のような質量1kgの直方体の物体を考えた時に重力加速度を9.8m/s2とすると、面aにはたらく圧力は、次のように計算します。
直方体の物体の重さ、つまり物体にはたらく重力は、1.0×9.8
面aは、面積が0.70×0.50で計算できるので、
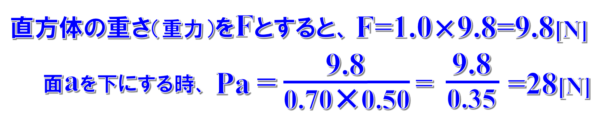
圧力は28パスカルとなります。
同じように、面b、面cを下にした時の圧力を計算すると、
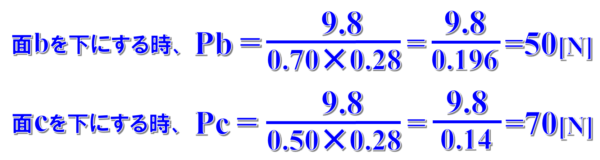
面bは、50パスカル
面cは、70パスカル
となって、面積が小さい方が圧力が大きくなることが数値計算によって示されます。
圧力の単位について
圧力の単位には、他にヘクトパスカルや気圧などが利用されます。
1ヘクトパスカル(hPa)は102パスカル。1気圧は約1.013×105Pa
または1013ヘクトパスカル(hPa)となります。
大気圧について
気体の圧力は、空間を飛んでいるきわめて多数の分子が壁に次々と衝突することによって発生します。

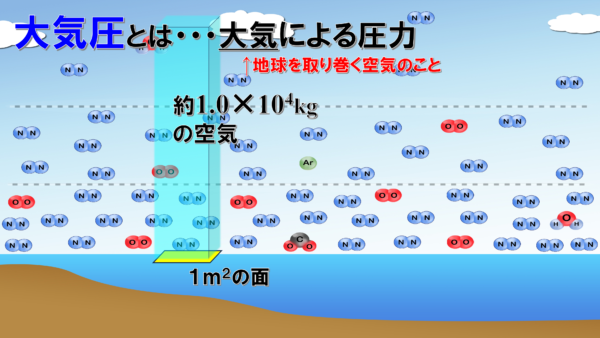
この気体の圧力のうち、特に大気(=地球を取り巻く空気)による圧力を大気圧といいます。
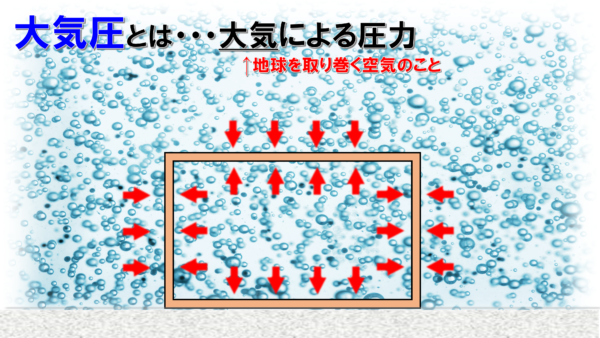
大気圧は海面の高さでは1気圧であると言われています。これは、面積1m2の地面に、質量が約1.0×104kgの空気が乗っかっていることを意味しています。
水圧について
気体や液体のことを総称して流体と言いますが、流体の圧力は、目に見える液体の様子を観察するとその特徴を確認することができます。
ここでは、水の圧力を見ていきます。
水の重さによって生じる圧力を水圧と言います。
次の実験によって、水圧について2つの特徴が確認できます。

水圧には、こういった特徴があります。
■参考動画
こちらの動画のように、
両端にゴム膜を固定した円筒のパイプを沈めると、ゴム膜が内側に凹んでいく様子が確認できます。
そして、左右のゴム膜は、同じだけ内側に押し込まれて凹んでいます。

これは、上下の方向で観察しても同じ深さでは同じだけ押し込まれます。
これより、同じ深さでは水圧はどの方向にも同じ大きさであることが確認できます。

それから、円筒パイプを沈めていくときに、水深が深くなっていくと、それだけゴム膜が大きく内側に押し込まれる様子が確認できます。

したがって、水圧は水深が深くなるほど大きくなることがわかります。
水圧の式
水圧の大きさは、水の密度をρとすると、水深h[m]では、

と表されます。
この式は、底面積がS、水深がh、水の密度がρの水柱の底面が及ぼす圧力を考えることで導かれます。

皆さんは、軽い円柱の容器の中に入った水を下から支えた時に、人に加わる圧力がいくつになるのかをイメージしてください。
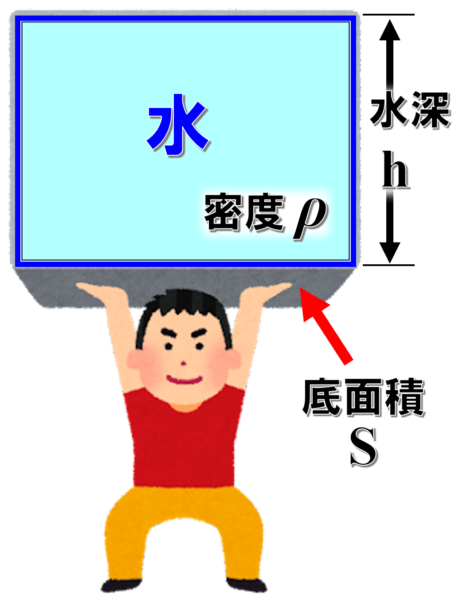
水の圧力は、まずは水の重さ(重力)を計算します。それを面積で割れば、単位面積あたりの力、つまり圧力になります。

そこで、水圧の式を導くためにまずは水の重さから求めていきます。
水の重さは、質量×重力加速度です。
![]()
水の密度は1㎥あたりの質量なので、質量は、密度×体積で求まります。
![]()
体積は底面積×高さですから、S×h
![]()
したがって、水の重さはρShgとなります。
水圧は、水の圧力ですから、水の重さを面積で割って1㎡あたりの力として算出すると、p=ρhgとなります。
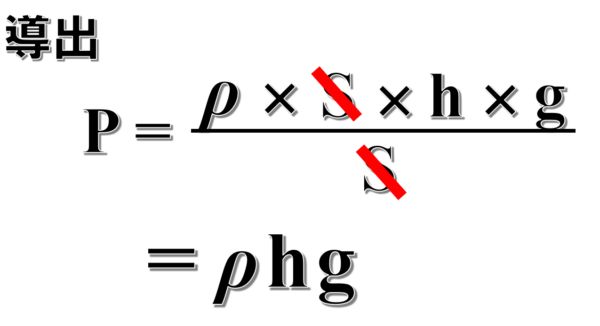
これが水による圧力です。
水圧の式を見ると、ρは水の密度で一定の値、gは重力加速度でほぼ一定の値となるので、水圧は水の深さに比例することがわかります。


つまり水圧は、水深によって決まるということです。
また、水圧は水の入っている容器の形や大きさとは関係がありません。
水圧の計算例
地球上では、大気の圧力が存在するので、水深h[m]で物体が受ける圧力をp’とすると、p’は大気の圧力P0と水圧の和として求められます。
![]()
例えば、水深5.0mの池の底の圧力p’は、水の密度を1.0×103kg/m3、水面での大気圧を1.0×105、重力加速度の大きさを9.8m/s2とすると、次のように計算できます。

これより、p’を求めると、1.5×105Paとなります。














