
目次
はじめに
今回は摩擦力を受ける運動について解説します。
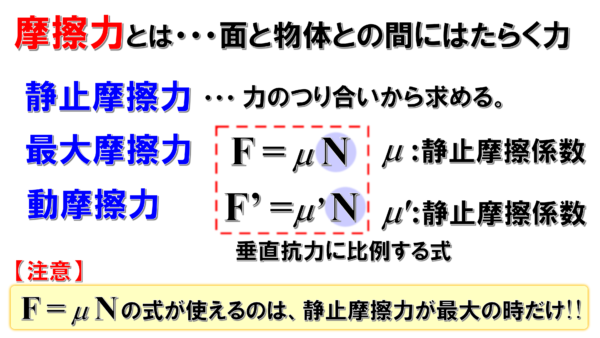
摩擦力とは、面と物体との間にはたらく力のことです。

粗い面をすべる物体がやがて静止するのは、面が物体に対して運動を妨げる向きに摩擦力を及ぼしているからです。

3つの摩擦力
この面にはたらく力である摩擦力ですが、摩擦力には3つの呼び名があります。

1つ目が静止摩擦力という力、
2つ目が静止摩擦力の特別な状況にある時の最大摩擦力、
3つ目が動摩擦力です。
そして、最大摩擦力と動摩擦力には式が用意されています。
最大摩擦力は、f=μN 、Nは垂直抗力です。
動摩擦力については、f’を動摩擦力とすると、f’=μ’N…
μが静止摩擦係数、μ’を動摩擦係数と呼んでいます。

これらの式は、垂直抗力に比例するという式で、実験的に示された式なので実験式として覚えておいてください。
一方、静止摩擦力には式がありません。これは後で解説しますが、力のつり合いから求めないといけません。

よく静止摩擦力を求めなさいと言われて、f=μNの式を使う人がいますが、この式は最大摩擦力を求めるときしか使えません。
最大摩擦力は静止摩擦力が特別な場合にあるときの摩擦力です。静止摩擦力が最大の時が最大摩擦力です。ですから、この時しかf=μNの式は使えません。
具体例
例えば、学校のグラウンドでこれからサッカーを始めるとします。

そこでグラウンドにあるサッカーゴールを移動させます。
このサッカーゴールですが、非常に重たいので1人の力では動かせません。
それは、ゴールポストの接触面から、摩擦力がはたらいているからです。

もしも、氷の上など摩擦のない平面だったら、ツルツルすべらせてゴールを運ぶことが出来たかもしれませんが…

現実にはそうはいきません。
この時、この人が加えた1の力に対して、逆向きに1の力が摩擦力としてはたらきます。

したがって、全体でみれば、このサッカーゴールには力がはたらいていないのと同じことになります。だからゴールは動きません。
そこで、友だちに手伝ってもらって2人で押したとします。

しかし、それでも動かなかったとします。

そうすると、その時の摩擦力は、2となります。
このようにして静止している物体に対する摩擦力は、力のつり合いを考えて求めます。

3人で押しても動かない・・・

この時の摩擦力は3・・・
こういうときの摩擦力のことを静止摩擦力と呼びます。
したがって、静止摩擦力というのは、公式から求められるものではなくて力のつり合いから求めるものになります。
そして、3人、4人、5人と人を増やしていくとやがて、ゴールが動き始める瞬間が訪れます。

それが最大摩擦力です。
その時の摩擦力は、f=μN となって、垂直抗力に比例した式で求めることが出来ます。
そして、サッカーゴール動いている時にはたらく摩擦力が動摩擦力です。

動摩擦力と静止摩擦力の大きさについては、皆さんも経験的に知っているのではないでしょうか・・・??
一度物体が動き始めると、動き始める前よりも楽に動かせますよね。
したがって、動摩擦力よりも静止摩擦力の方が大きくなります。

問題解説
それでは、実際に問題を解いていきます。
例題1
あらい水平面上に重さ50Nの物体が置いてある。これに対して水平方向に徐々に大きな力を加えていったところ、30Nを超えた直後に物体は動き始めた。

(1)物体と水平面との間の静止摩擦係数はいくらか。
まずは物体にはたらく力を整理しておきます。
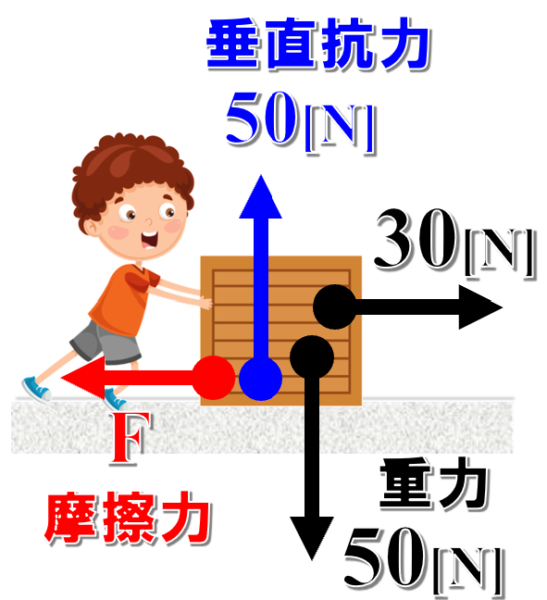
物体には下向きにはたらく50Nの重力、そして、それを支える垂直抗力が50N
そして、右向きに物体を引く力。その力と反対向きにはたらく摩擦力。

物体にはたらく力は以上の4つです。

ここでは、物体に加える力(引く力)を1N、2N・・・と、徐々に大きくして言って、30Nを超えたところで動き始めたわけです。
したがって、ここでは最大摩擦力は30Nと考えます。
静止摩擦係数は、f=μN の式より、fは30、Nに50を代入すると…
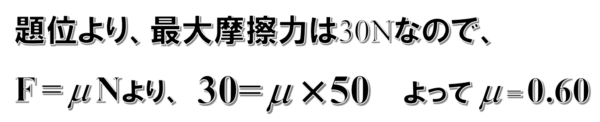
したがって、静止摩擦係数μは、0.6となります。
(2)物体に対して水平方向に15Nの力を加えるとき、物体にはたらく静止摩擦力の大きさは何Nか。
物体は30Nを超える力を加えないと動かないわけですから、この時の静止摩擦力は、力のつり合いから求めます。
つまり、水平方向については、物体に加えた力と静止摩擦力の大きさは等しいので、この時の静止摩擦力は15Nとなります。
![]()
例題2
それでは次の問題に移ります。
水平な台の上に質量10kgの物体を置き、水平方向にFの力を加えたところ、物体は一定の加速度0.80m/s2で運動した。物体と台の面との動摩擦係数は0.50である。重力加速度の大きさは9.8m/s2とする。

(1)このとき物体にはたらく動摩擦力の大きさは何Nか。
動摩擦力は、垂直抗力に比例する力なので、まずは、物体にはたらく力を書き出して、垂直抗力の大きさから求めていきます。
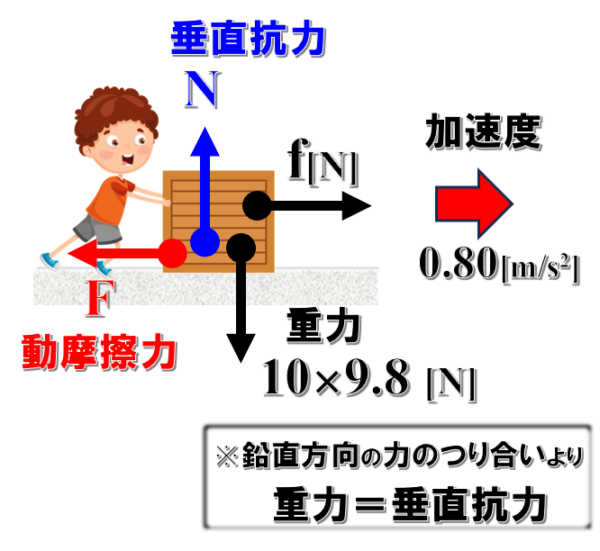
すると、物体にはたらく力は、重力と垂直抗力、そして動摩擦力と水平方向の力Fの4つで、重力の大きさは、質量10kg×重力加速度9.8で98Nです。
鉛直方向については、物体の運動状態は変化しないので、力のつり合いの式より、垂直抗力の大きさは重力と同じで98Nとなります。
これより、動摩擦力は
![]()
したがって、49Nになります。
(2)加えた力Fは何Nか。
物体は右向きに一定の加速度0.80m/s2で運動しているので、運動方向に関して運動方程式を立てます。

運動方程式ma=Fの式は、左辺に着目する物体の質量と加速度、右辺に物体にはたらく力の合力で表せる因果関係を示す式です。
そうすると…

質量10kgの物体が0.80m/s2の加速度で運動するのは、右向きの力Fと左向きの動摩擦力が作用するからだ。
という式が立てられます。
これより、Fは57Nとなります。
例題3
最後の問題です。
14m/sの速さで走っていたトラックが急ブレーキをかけたら、一定の割合で減速し、やがて停止した。車輪と地面との間の動摩擦係数を0.50、重力加速度の大きさを9.8m/s2とする。

(1)このときのトラックの加速度は何m/s2か。トラックが初めに走っていた向きを正の向きとする。
今までの問題とは少し違ったタイプの問題ですが、物体の運動に関する問題ですので、解法の手順は変わりません。

まずは、物体にトラックにはたらく力から考えていきます。
トラックには、重力と垂直抗力、そして進行方向とは逆向きに動摩擦力がはたらきます。


14m/sで走っていたトラックはブレーキをかけることで、動摩擦力を利用して減速しているわけですね。
鉛直方向については、重力と垂直抗力がはたらきますが、トラックの質量はわからないので、とりあえずmとしておくと、
重力の大きさは9.8m[N]、したがって垂直抗力の大きさは9.8m[N]
動摩擦力の大きさは次のようになります。
![]()
次に、この時の運動方程式を考えてみます。
トラックの加速度をaとすると…
![]()
質量m[kg]のトラックに加速度a[m/s2] を生じさせたのは、4.9m[N]の動摩擦力が負の向きに働いたからである。

トラックが初めに走っていた向きを正の向きとすると、動摩擦力は逆向きに働く力なので、マイナスの符号をつけることに注意してください。
この式の両辺にmがあるので、両辺をmで割ってa を求めると、

加速度a は、-4.9[m/s2]となります。
やや難易度の高い問題だったと思います。
次の問題もなかなか難しいので注意して見て行ってください。
(2)番、急ブレーキをかけてから、停止するまでにトラックが進んだ距離は何mか。

ブレーキをかけてから、トラックが停止するまでの距離を求めないといけない訳ですが、どこから手を付けたら良いかがわからないですねぇ・・・
まずは、問題文をよく見てみると、
トラックが急ブレーキをかけてから一定の割合で減速し…
とあります。

ここに問題を解くための手がかりがあります。

トラックが一定の割合で減速する・・・
これは加速度が一定であるということを意味してますから、ブレーキをかけてから停止するまでのトラックは等加速度運動をしています。

だから、ここでは等加速度運動の式を使います。
加速度は(1)番で既に求めています。
等加速度運動の式は3つありますが、今回は3つ目の式を使います。
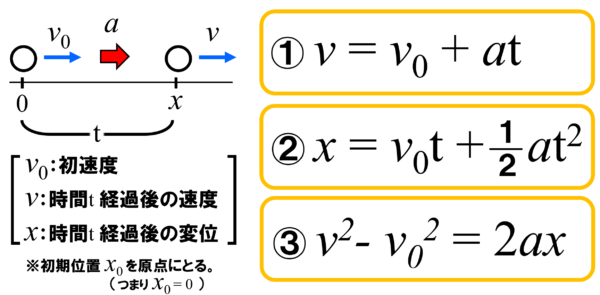
最初トラックは14m/sで走っていて、ブレーキをかけることで減速して、やがて停止します。

停止するですから、このときの速度は0[m/s]です。
したがって、初速度v0は14m/sで、vは0m/sです。
そして、進んだ距離をxとすると、2掛ける加速度は-4.9そして掛けるx
![]()
この式からxを求めます。
そうすると、進んだ距離は、20mとなります。
この問題は、v=v0+atの式から時間tを求めて、求めた時間からx=v0t+1/2at2の式を使って、xを求めるという方法もありますが、3つ目の式を使うと、1つの数式で解答に辿り着くことができます。
今回の解説は以上となります。














