
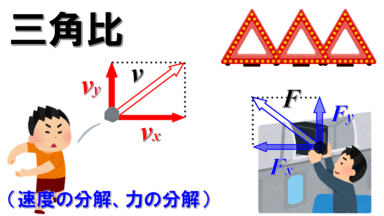
はじめに
ここでは力の合成と分解について解説します。
力の合成

1つの物体に2つ、またはそれ以上の力が同時にはたらくとき、これらの力と同じはたらきをする1つの力を求めることができます。この1つの力を求めることを力の合成といい、合成された力を合力といいます。
今から物体に2つの力がはたらく場合について、力の合成方法を確認していきます。
2つの力が平行にはたらく場合
まずは2つの力が平行にはたらく場合からです。
力を図で表現するときは、力の大きさを線の長さに対応させて、矢印の方向が力の向きであることを示します。
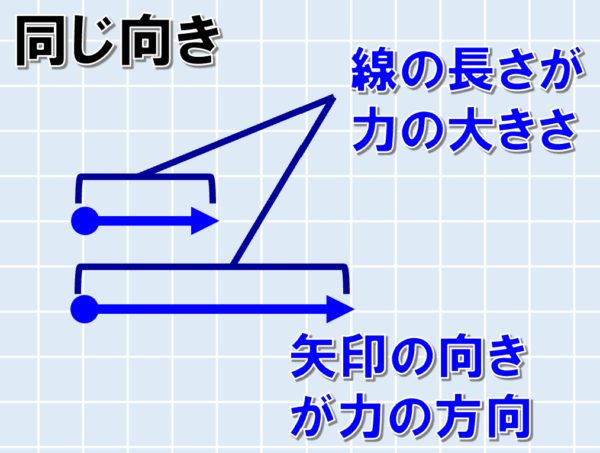

力は大きさと向きを持つ物理量なので、ベクトル量に分類されます。
また、力を図で描く時は、どちらの物体にどこから力が発生しているのかをわかりやすくするために作用点を書きます。
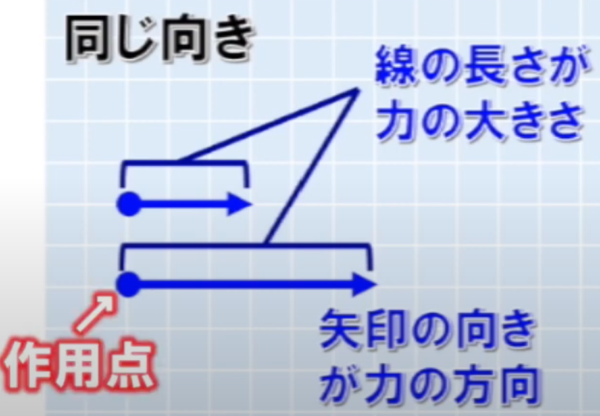
2つの力が同じ方向の場合、合力の大きさは2力の大きさの和となり、向きは初めと同じ向きになります。
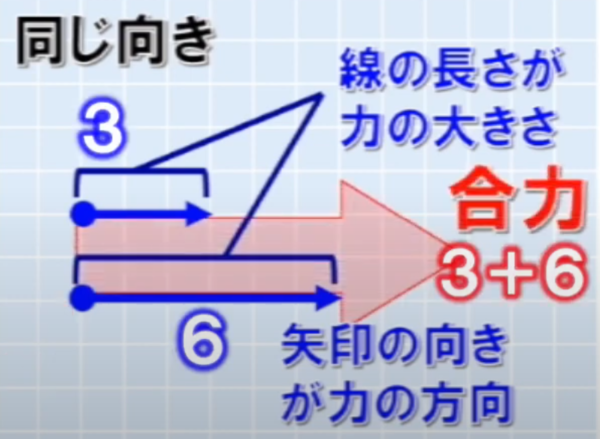
2つの力の方向が逆向きの場合、合力の大きさは2力の大きさの差となり、向きは2力の内、大きな力の方向となります。
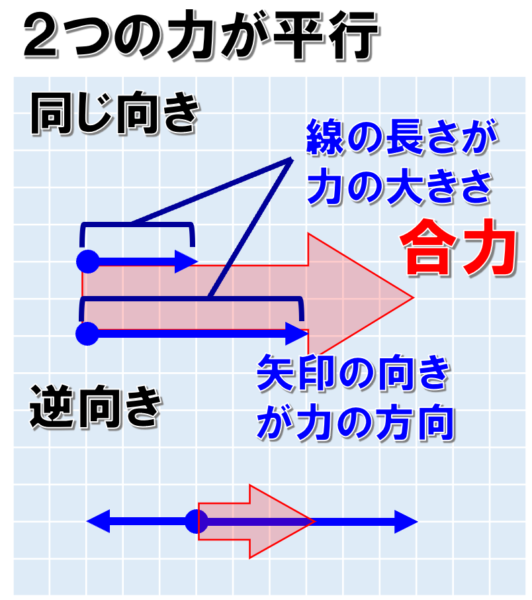
2つの力が平行でない場合
次に、2つの力が平行でない場合の力の合成方法を確認します。
今、物体に平行ではない2つの力が働いているとします。
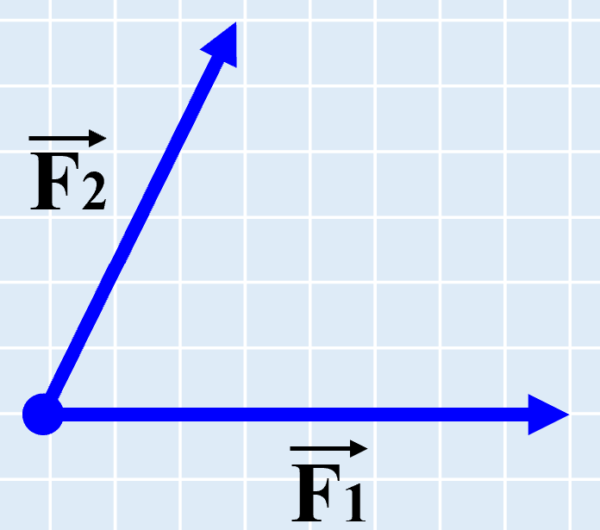
ベクトル量を表現する場合は、図のようにアルファベットの上に矢印を表記して、それがベクトル量であることを示し、F1ベクトル、F2ベクトルと呼んだりします。
F1ベクトル、F2ベクトルを合成する方法は2つあり、別々に紹介していきます。
平行四辺形を書く方法
まずは、平行四辺形を書く方法です。
物体にF1ベクトルとF2ベクトルがはたらく時、2つのベクトルに平行な線を書いて、平行四辺形を描きます。
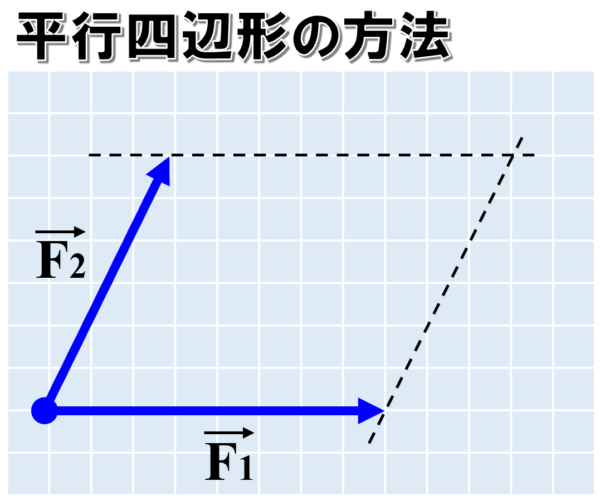
次に、平行四辺形に対角線を引きます。
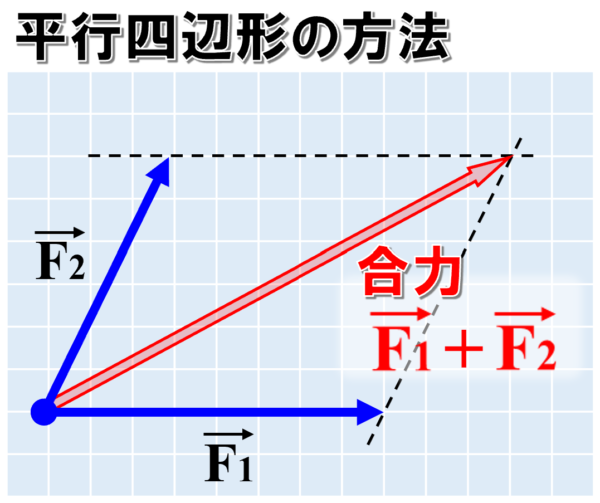

この時、矢印で描かれた対角線が合力です。
力をつなぐ方法
力の合成をする方法は、これとは別に、力をつなぐ方法があります。
F1ベクトルの始点をF2ベクトルの終点を合わせ、
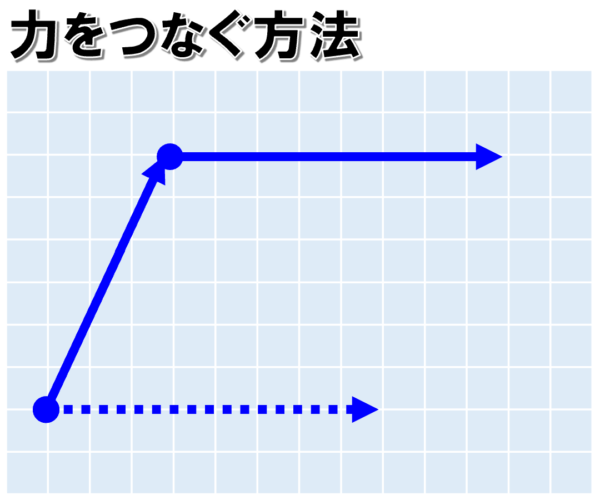
F2ベクトルの始点からF1の終点へ線を引きます。
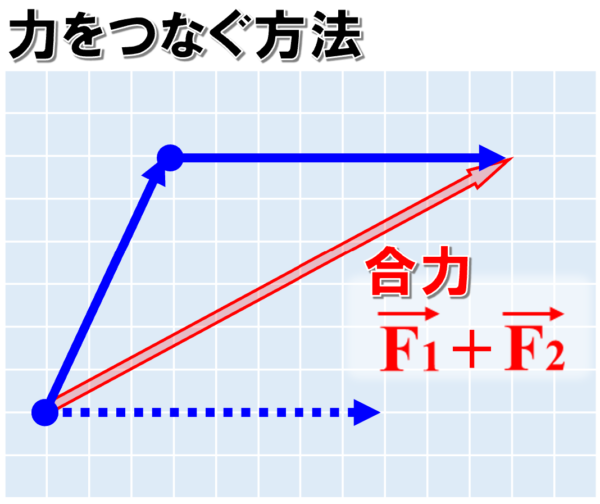
こうすることで、合力を求めることができます。
力の分解
次に力の分解に移ります。

力の合成とは逆に、1つの力を、それと同じはたらきをする2つ、またはそれ以上の力にわけることができます。これを力の分解といい、分けられた力を分力といいます。
ここでは1つの力を2方向に分解する方法を確認していきます。
力の分解は、分解する2方向の選び方によって何通りでも考えられるので、
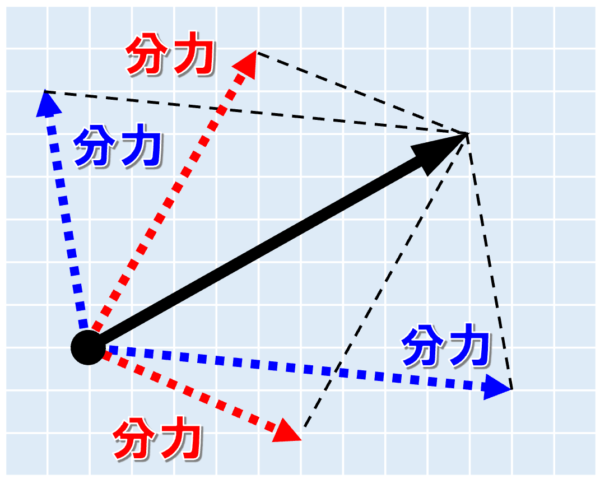
まずは、どの方向に力を分解するのかを決定します。

力を分解する時は、互いに垂直な2方向に分解すると便利なことが多いので、ここではx軸方向とy軸方向に分解することにします。
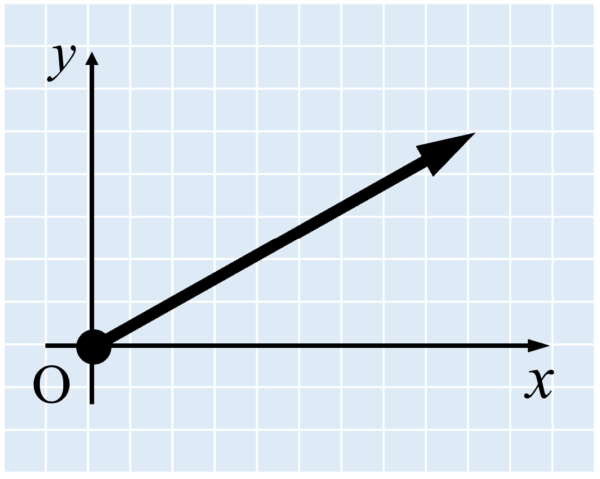
この時に、x軸とy軸に平行な線を書いて、平行四辺形を描きます。
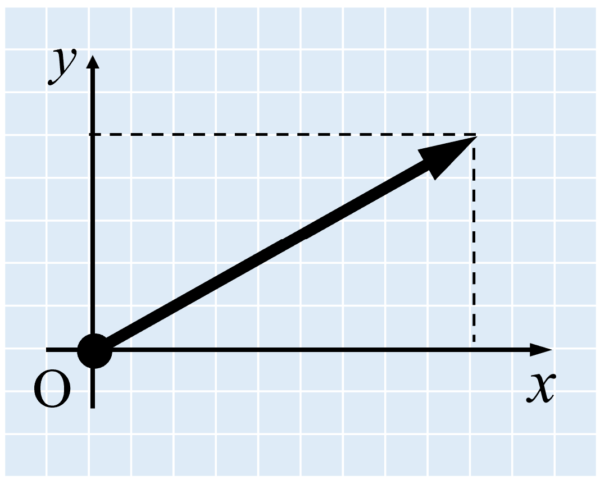
それから次のように矢印を描くと、それぞれがFベクトルの分力であるF1ベクトルとF2ベクトルになります。
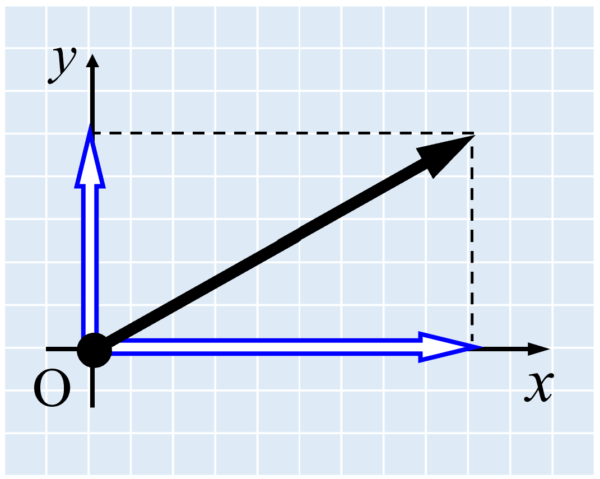
もしも図の1目盛りが1Nの力の大きさに対応しているなら、x軸方向の分力は9N、y軸方向の分力は5Nとなり、それぞれを力Fのx成分、y成分といいます。
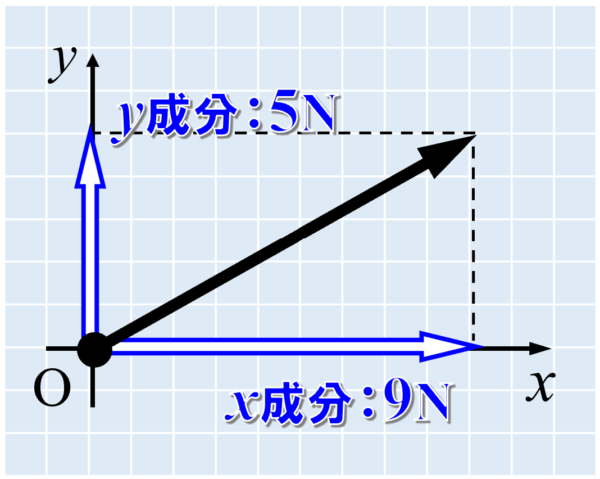
x成分、y成分は、分力の大きさに、向きを表す正・負の符号をつけた値で表されます。
したがって、次のような図では、x成分は負の値になります。
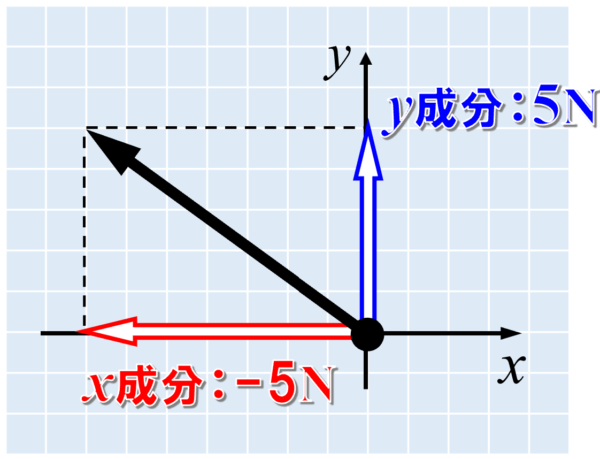
また、力Fのx成分をFx, y成分をFyとすると、力Fの大きさは、ルートFxの2乗プラスFyの2乗の式で表すことができます。
![]()
これで力の合成と分解の解説は以上となります。
これより先に合力や分力を取り扱う場合は三角比を利用します。
数学で三角比をまだ学習していない人や三角比を用いた力の分解に自信のない方は、こちらの記事に進んでください。







-384x216.jpg)







