はじめに
それでは2番目に行きます。抵抗の合成をやっていきましょう。

ああ、知ってる知ってる!
という人もいると思いますが…

しかし、基本的には回路の問題を解く時には、合成の知識っていうのはそれほど必要はないですし、あまり乱用しない方がいいです。
しかし、この合成を考える時に回路として重要な考え方があるんです。
回路の解法②(抵抗の合成)
まず抵抗の直列接続。これの合成から考えていきたいと思います。
直列接続の合成

R1、R2っていう抵抗があります。

要するに、これを1個の抵抗と考えると、大体どのぐらいの抵抗に相当するんでしょうか!?
という感じです。
1個の抵抗に置き直したら、どんな値になりますか?
これをやりましょう。では行きます。


これは、つまり左の回路と右の回路は同値だということです。
同じ意味だということです。
例えば、左の図で抵抗R1に電流がI 流れていると仮に仮定します。

そうすると、もう一つの抵抗にも間違いなく I 流れているはずです。

抵抗があっても電流は減りません。

通りにくくなっただけですから。
全体として流れている量は変わりません。
左の回路と右の回路が同じだということは、電源の電圧Vは一秒間当たりIクーロンの電荷を持ち上げてるわけですから、それと同じでなければいけません。


さあ、それでは、電位の式を書いてみたいと思います。
電 位 の式です。
まずは左の図からです。こちらの電位の式というのは、次のようになります。

抵抗R1の両端の電圧って、IR1ですよね。
抵抗R2の両端の電圧ってIR2ですよね。

ちょっとまってください。
回路について既に学習した人は、これをキルヒホッフの法則だとか、回路方程式だとか、いろんな名前で教わってると思うんです。

私は、電位の式と一番簡単な言葉で言ってるんですけど、言葉はどうでもいいんです。
大事なのは何か!?

どんな概念なのか!?

これ(IR2)って、何なんですか?
簡単に言うと、回路の中に+1クーロンがあって、R2の下の方から上の方にいくとIR2高いんです。
さらに次の抵抗を見てみると、IR1、高いんです。

そんな高低差を付けたのは、誰!?
って言ってるんです。

お前だ!

それがこの式(V=iR1+iR2)です。
そういう意味なんです。
では同じようにもう一つの回路も考えてみます。

IR高いんです。
それはこれ(V)のせいですよね。
ですから、こちらの電位の式は次のようになります。

これでオッケーでしょう。
そうすると、このV同じなんです。
同じ回路ですから。
そうなると、
![]()
![]()
Rから書くと、こういう式が出来上がりました。

覚えててもいいけど、あんまり役に立たない式です。

当たり前じゃないか!?
っていうのでまさに終わりです。

私は、そんなことを言いたいから、時間使ってこんな話したんじゃないんです。
さっき言った通り、
新しいことを勉強しながら、回路の解法をちゃんと確認していきましょう。
って言ったんです。

今、私は何をやったんですか??
これ何をやっているんですか??
よく聞いててください。
これは抵抗回路です。

抵抗回路だけれども、別にエネルギーのこと何も聞いてない訳ですよ。
抵抗そのものをいじくってる訳じゃないですよね。
これを半分に切ったとかそういうことをやってるわけじゃないです。
太さを太くしたとか、そんなこと言ってるんじゃないです。

そうか、それならV=IRっていう式をちゃんと使えば、この問題が解けるはずだ!
と考えたんです。
ですから、この回路図とこの回路図を書いた瞬間に、

よしV=IRをとりあえず3回立てよう!
抵抗が3つあるんです。
だからV=IRを3つ立てようと思ったんです。
ところが残念なことに、最初に与えられていたのはR1、R2だけです。

それじゃあ、V=IRの式を立てられないですねぇ。
そこで、抵抗を流れる電流を I アンペアって置いてみたんです。

なぜ置くのかってことも、ちゃんと考えないといけません。
そのおかげで、R1を流れる電流を I と置けばR2を流れる電流も I です。

だから、IR1, IR2て書けるんです。
抵抗R1, R2を流れる電流が I なら、抵抗Rを流れる電流も I でないといけません。
だから、IRと書くことができます。
抵抗R1を流れる電流が I だと抵抗R2には I 流れる。

何をやったんですか??
こういうのを 電 流 保 存 と言います。
例えば、次のような分岐点に電流が流れていた時に、
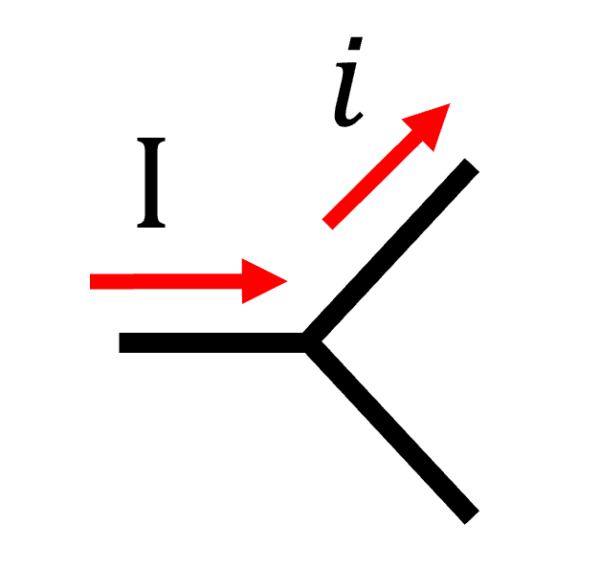

右向きに流れる電流 I と分岐してから流れる電流 i は等しくないですよね。
斜め下方向に流れてるかもしれないですからね。

だから電流保存を考えたわけです。
それでV=IRを3つ考えながら、その時、電流保存も考えた。

電流保存によると、電流Iは全て同じだ!

そして、何を立てたか!?
電位の式を立てたんです。

じゃあ先生それ全部覚えるんですか!?
そのステップを全部覚えていくんですか!?

いいえ。覚えるのではありません。
もう一回言います。

皆さんに、ぜひ気付いてほしいんです。
回路図をみたら抵抗が3つあります。
だから3回 V=IRを立てなければいけない。
しかし、与えられたのは抵抗の値だけですから、
Iを仮定しようとした。

その I を仮定するとき電流保存を考えた。
それで I を仮定していった。

そのために V=IR が使えるようになったから、3つの抵抗を使いながら電位の関係式を立てて答えを出した。
と言ってるんです。

だんだんと当たり前になってきましたか…??
それでは、種明かしをしていきます。
前回の記事で抵抗の式を書きました。コンデンサーの式書きました。
□前回の記事

そんなの知ってますよ!

でも回路は苦手なんです!
っていう人が多い。
それで…

そういう人っていうのは式の使い方がイマイチ見えてないんだ。
と言いました。
エネルギーは、エネルギーの式として、
今は、一番最後に説明したエネルギーも関係ない。
抵抗そのものの式も関係ない。

だから、V=IRをいかに使うかですよね。
だから、V=IRを3つ、ぽっぽっぽって書きました。

V=IRの式はすべての抵抗について成り立つんですよね?
だからこれ3個立てるんですよね?

最終的には、合成抵抗Rが欲しいんですよね??
それじゃあ電流保存と電位の関係式を考えればいいんです。

どうですか?
電流保存を考えた上で電位の関係式立てましたね。
だから、出来ました。

これがV=IRの正しい使い方です。

V=IRを知っていれば出来る!
ってことじゃないでしょう。

要は、電圧と電流と抵抗の間には、V=IRという関係式が成り立ってるわけです。
それしかないんです。
それを使っていけばいいだけです。

ところが、なかなか、みんなそうやってくれないんです。
並列と言うと、何対何に電流が分かれるとかって考えてしまう。

そんなものはありません。
そういう結論を急ぐ解法を身につけようとしてしまうんです。
だから、

並列とか直列とかが分からない!
っていう風になってしまう。
実際の例で言うと、テレビの取扱説明書とかの裏を見ると回路図が書いてあります。
ビックリするくらい、ものすごい回路図です。

じゃあその回路図を見て、これとこれが並列だからって、分かりますか?
もう面倒くさくて、どれとどれが並列で、どれとどれが直列かさっぱり分かりませんよ。
直列とか並列とか、そんな事はどうでもいいんです。
要は、今までに私が直列接続について説明しました。

けれども、これは直列だからどうのこうのとは言ってないですよね。
直列だからこれとこれを足したものが、これに等しいとは言ってないですよね。

1クーロンを持った人が、回路の中をちょっと歩いて行ってみたんです。そうしたら高いところ行っちゃったんです。「高いところに行ったのは誰のせい!」ってあんただね。
って、
説明しただけですから。
そういうふうに教科書にも、こういう風な抵抗の合成とか、色々あると思うんですが、どうしても、

あぁ直列接続だったらただ足せばいいんだな!
っていう…

この結論ばかりを見てしまうんです。
こんな式は覚えようが覚えまいがどうでもいいと思うんです。
それよりも教科書に、今回のような証明が書いてあります。

なんで、こんな式になったのか!?

なんでここは Iって置いたんだ!?
とか、そこを考えてください。
並列接続の合成

もうここまで説明すると、だんだん回路というものが優しく感じてきます。
次の2つの回路が同じ回路である!
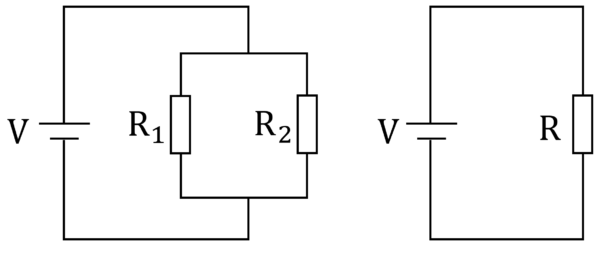
と考えます。

それでは行きましょう。
V=IR3つ立てないといけませんが…

困りましたねぇ…。これ!
仕方ないのでここをI1と置きましょう。そして、ここをI2と置きましょう。
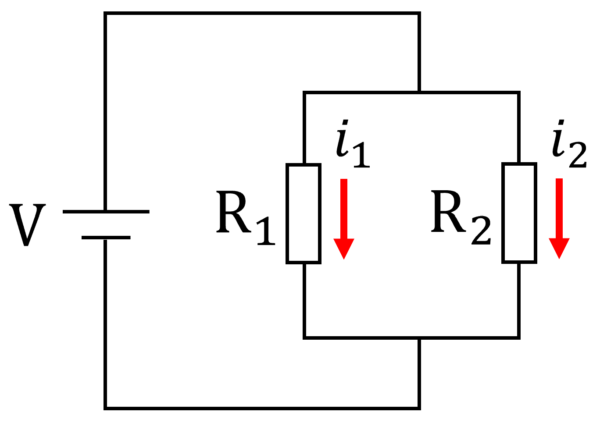

抵抗R1とR2に分岐する前の電流は、I1+I2ですよね。
それが2手に分かれている。
2つの回路は同値であるということは、抵抗Rを流れる電流っていうのは、
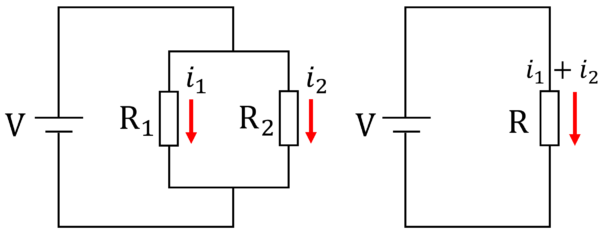

I1+I2とやっていいですね。
抵抗R1と抵抗R2を一つにした回路ですから。

次にV=IRを立てていきます。
並列回路の方は、次のようになります。
合成回路の方は、こうです。
![]()

プラス1クーロンを持った人が、たったかたったかやってきて、高いところ行ったぁ…、それは、あんたのせい。

並列だからどうのこうのとか、言っちゃ駄目です。Vは、1クーロンあたりの位置エネルギーのことですから。
それでは、邪魔なものを消しています。
I1, I2 は次のように書き換えることが出来ます。
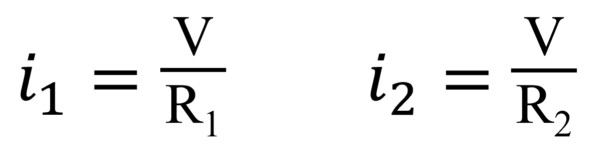
合成回路の式も同じように変形すると…
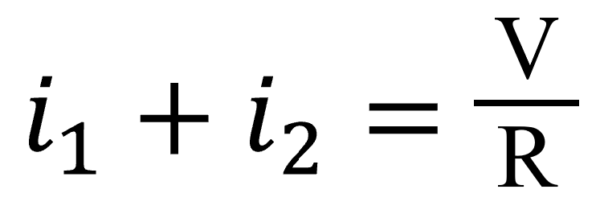
となります。
![]()

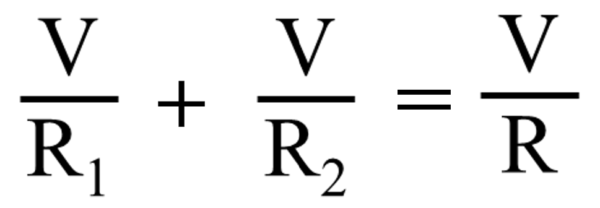

しかし、元は電流保存から考えた式です。
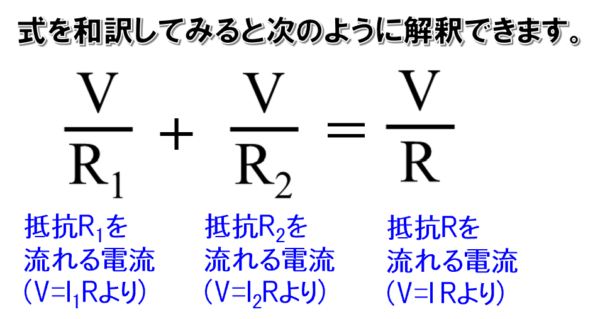
抵抗R1で流れてる電流と抵抗R2に流れる電流が全体に流れる電流に等しい!
って書いてあるだけですよね。

だからV=IRを3つ立てた。

I1とI2を勝手に決めた。
だから、消去していった。
それで終わりです。
やってみると簡単だって分かります。


ですが、どうしてもみんなこの結論を覚えるんです。
でも私は、この結論はあんまり好きじゃないんです。

好き嫌いなんてどうでもいいよ!
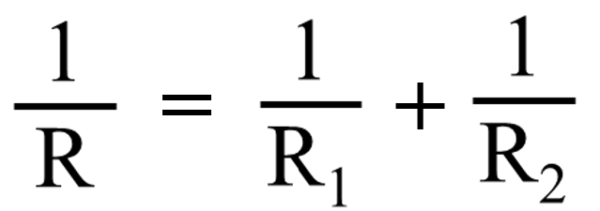

大体、これは和訳できないじゃないですか!?
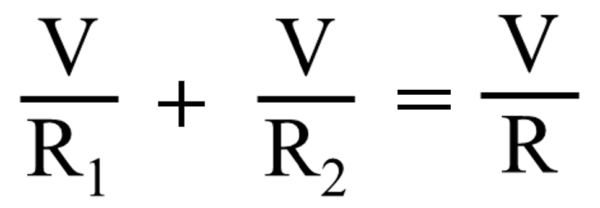
こちらは和訳できます。

流れてる電流を足したものが等しいですよ!
電流保存のことです!
って言えますよね。

ですから、一個手前の式が頭に入っているか?
どうってことないと思うんですけど、だから合成抵抗の式は、覚えてもいいし覚えなくてもいい式です。

ただ多くの人には、数式で示したことだけがこう残ってしまう…
そして、

あぁそうか!
これ覚えよう!
となってしまう。
なんで、こんな解説をしているのかっていうと…、

回路の勉強をしているんです。
決して合成抵抗とかの公式を導こうとしているのではない!
そう捉えてください。

ついでに導いてみた!
という風に思ってください。