はじめに

さあ、ようやくこうやってガウスの法則が理解できたので、平面に電荷を拡張することができるようになりました。
□前回の記事
やってみましょう。
コンデンサーの基本式
極板間の電場について

平面にどんな電荷があるのか!?
ということ、そして

どうやら平面であっても式は作れそうだ!

では、その時にこの周りにどんな電気力線ができるのか?
ということを考えます。
上と下の区別はないですよね。重力とかは考えないことにします。
ガウスの法則より、

プラスQクーロンからは4πkQ本しか出てかない…
2πkQ本ずつ…、2本の矢印で表現してみます。

すると、こうなるでしょうねぇ…

実際は、両端の電気力線は外側に広がっていきますが、

平行板コンデンサーでは、全体の性能に大きな影響を与えないものとして、ここでは外側の曲がった部分は考えないものとしています。



そうすると、この場合の電気力線はどうなるか?
これもプラス1クーロンをばらまけばいいので、プラス1クーロンの電荷をばらまくとこうなります。


それでは、この2枚の鉄板を,上下に同じところに置いたら、どうなるんですかねぇ…??
やってみましょう。



もちろん2πkQ本です。
ここも2πkQ本になります。

それでは行きます。この2枚の鉄板を上下重ねたんです。そうすると、どういうことが起きるかです。

よ~く考えてください。
これは電気力線ですけど、元々これは力です。

相殺しますねぇ。
力はベクトルですから。
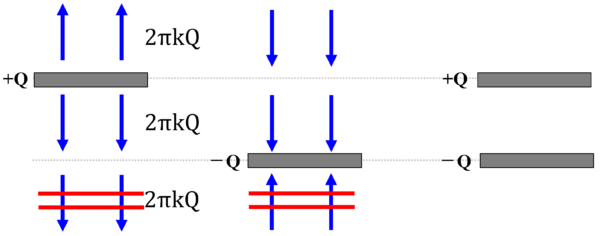
同じように上向き2本下向き2本、相殺します。
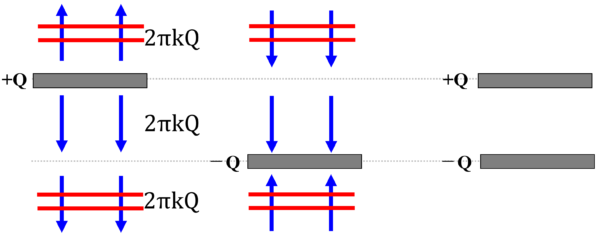

下向き2本下向き2本…
真ん中は…こうです。
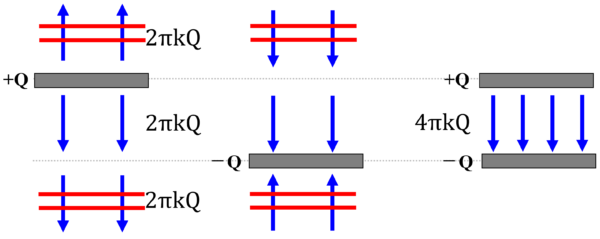

そして上にはない。
下にもない!
こういう状態なんです。そして本数は、全体で4πkQ本っていう…

こういう状態がコンデンサーなんですねぇ…
コンデンサーっていうのは、外部に電気力線ができないんですね。
それで内部に4πkQ…。

ガウスの法則を破ってないですねぇ…
プラスQクーロンから出た4πkQ本ですね。こうなるんです。

それがどうした??
ということなんですが…

電気力線の本数は1㎡あたりの電場なんです。
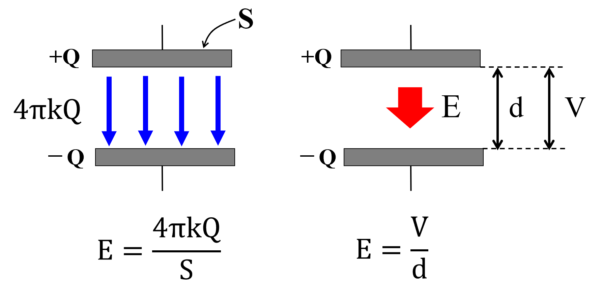
じゃあ、この極板面積Sで割って1㎡あたりに換算してあげれば電場が分かります。
コンデンサーの基本式の導出
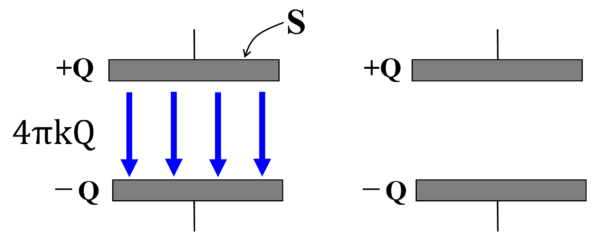

ここでガウスの法則を考えます。
そうすると、総本数4πkQ本です。1㎡あたりの本数が電場に等しいわけですから、コンデンサーの極板間にできている電場というのは単位面積当たりの電気力線総数に等しいということになります。
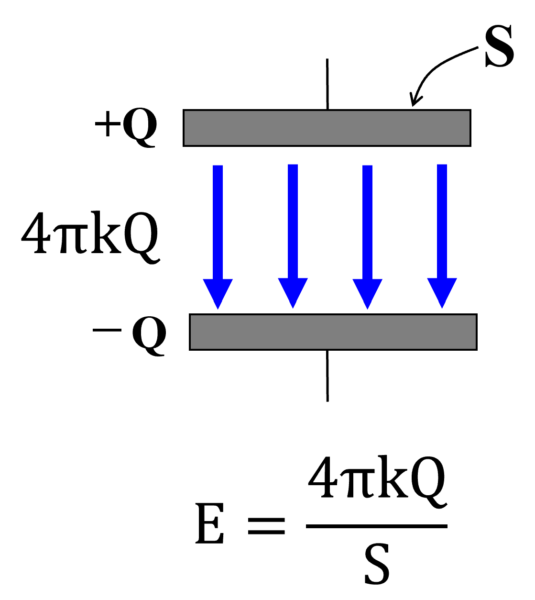

ここまでは、大丈夫だね。
一方、この考えから、この中にはこれだけの電場が出来上がった。
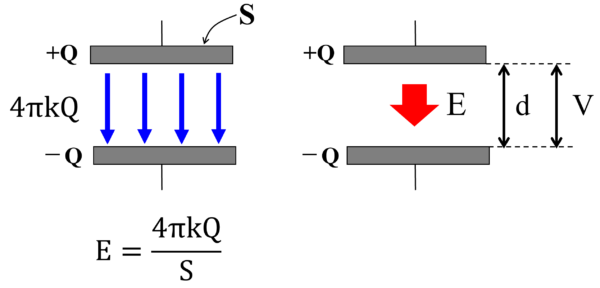

この時、極板の中にプラス1Cの電荷を持ってくると下向きにEという力を受けますが、そのEという力に逆らってdだけ持ち上げたとします。
それは、1クーロンあたりの位置エネルギーになります。

1クーロンあたりの位置エネルギーって電位に等しいですねぇ。
だから、V=Edが成り立つわけです。
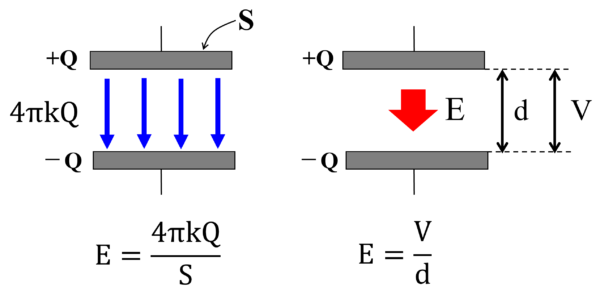

そうするとどんな式が出来上がるか…??
こんな式になります。
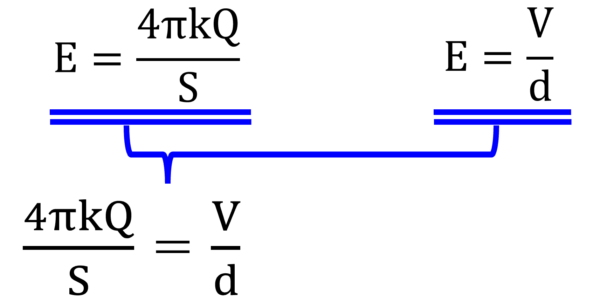

この式からQ=って変形すると…
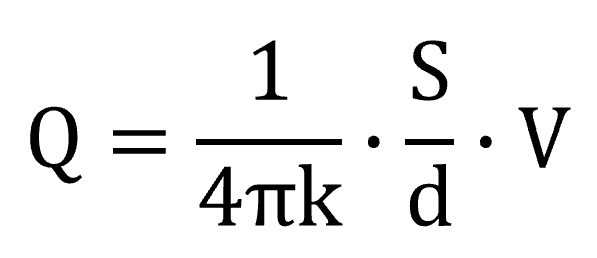
こうなりますね。

もう気づいてきましたか…??

4πk分の1は、定数ですねぇ…
これを毎回書くのは面倒くさいので、真空の場合は真空誘電率イプシロンゼロって置くんです。
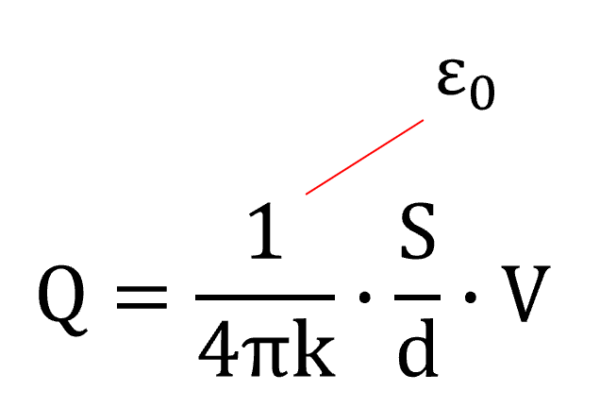


これがコンデンサの基本式と、呼ばれる式です。
コンデンサーの問題で点差がつく原因
それでは、続けて説明していきます。

まず1つ。心当たりの人は、ちゃんと聞いてください。
コンデンサー、


なぜこんな式が成り立つの??
って聞いた時に、

だって、それはもともと点電荷しかなかったところに、平面電荷を持ってきてガウスの法則をうまく利用したんですよ。
こういう風に言って欲しいわけです。

あぁ、そうだね。じゃあ、こういう風にしておけばいいよね。
っていうような話ができる。

ところが、どうしてQ=CV、C=…が成り立つの??
って言った時に先生、

それは成り立つに決まってるじゃないですか!?

そんなの。公式ですよ!
って言われると、

どうやって説明しようか…??
生徒からコンデンサーの問題を分からないって質問があったのに、その時に、それで済まされると、どうしようもありません。

冷静に考えてみて下さい。
コンデンサーの問題って、ものすごく点差がつくんです。

じゃあ、コンデンサーの問題が出たとき、全員が同じ点数になりますか?
って言うと、ならないでしょう。
みんなQ=CV、覚えてるんですよ。
でも同じ点数にならないです。

ところがそれを受験生は、頭の良し悪しだって言うんです。

そんな訳ない。
この程度のことしかやってないんですよ。

こんなので頭の良し悪しなんて絶対に分かりません。

教科書も何も見てないけど、自力で計算してみたら、こんな式を思いついた!
という人、

そんな人は頭がいいでしょねぇ。
でも、ほとんどの人が、そうじゃないですよね。

ただ、なぜ差がつくのか!?

Q=CVを覚えたのか、なぜQ=CVとなってCがイプシロンゼロd分のSと書けるかを知ってるか。その違いです。
それを覚えただけだと、記号の羅列と何も変わりませんから。

なぜこんなことを長々と言うのかと言うと…、
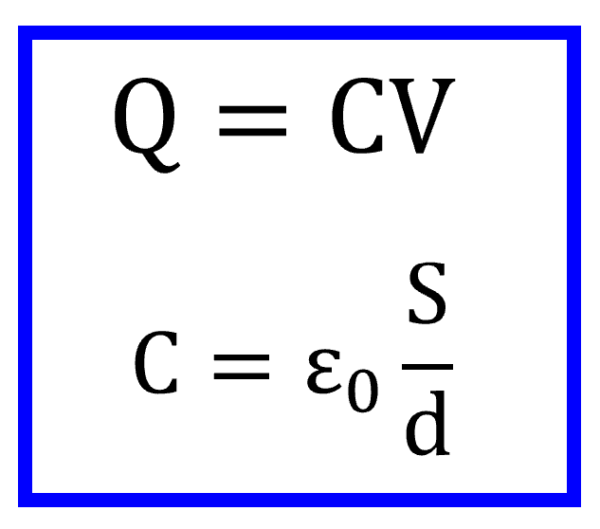

ところが、この式の中に電場が顔を見せてないんです。
電場って、すごく大切なんです。

例えば、電気抵抗だとV=IR。オームの法則っていうのは、教わったことあると思うんですが、あれで一番重要なのは電流I なんです。
電流I が最も大事で、式はV=IR 。

だから抵抗っていうのは、しゃれじゃないけど抵抗なく解けるんです。
結構楽に解けるんです。ところがコンデンサは、基本式がQ=CVです。

しかし大切な物理量は、極板間にできた電場なんです。
そういう理由で

抵抗に比べるとコンデンサーの方が嫌い!
という受験生が増えてくるんです。
それで、スイッチをカチャカチャカチャカチャ切り替えられると

もうどうなってるか、さっぱりわかんない!
ってなるんです。

でも電気力線引っ張ってみると、すぐ分かる。

そして何か公式なかったけ!?
って言うんですよ。

そんな公式はありません。
これしかない。

要は、公式の中に何か入れて、なんかごちゃごちゃごちゃごちゃ、ただやってるだけ!
っていう感じになってしまう。

大切なのは電場である。
だからガウスの法則という、点電荷から平面電荷に拡張するための法則をすっ飛ばしてしまうのは、どうしようもないことだから、

これを覚えて終わらせないということは、大変重要になってくるんです。
さぁ、こうやってコンデンサーというものが大体見えてきました。