はじめに
ここでは加速度の定義とv-tグラフにおける加速度を見ていきます。
動画による解説はこちら↓↓↓
加速度について
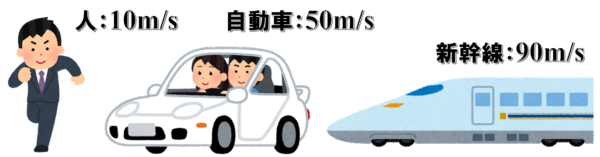
人、自動車、新幹線の速さは、全速力の場合、それぞれ10m/s、50m/s、90m/sです。

これらが同時にスタートして、2秒後に先頭を走っているのはどれでしょうか??
順位は意外にも、人、自動車、新幹線となります。
これは、人の速さが短時間で最大値になるのに対して、自動車や新幹線は長い時間をかけて、速さが増えるためです。

このように、物体の運動の様子を知るには、速度だけでなく「速度が時間の経過につれてどのように変化していくか?」を調べることも必要になってきます。
そこで出てくるのが加速度です。

加速度は、単位時間当たりの速度変化のことを言います。
速度が時間と共に変化する運動を加速度運動と言います。
高等学校では、ある時間で平均した平均の加速度や常に一定の加速度で運動する等加速度運動について学習します。
■平均の加速度
ここでは平均の加速度について考えてみます。
真っすぐな道路に停止していた車が動き出し、徐々にスピードに乗って加速したとします。
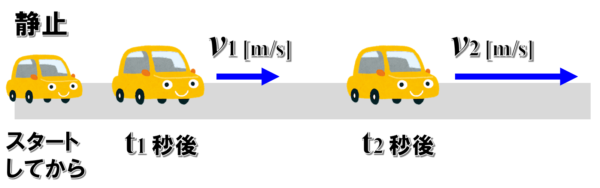
時刻t1 での車の速度をv1 とし、t2 での速度をv2 とした時について考えてみます。
経過時間をΔtとして、時間の変化量を計算すると、
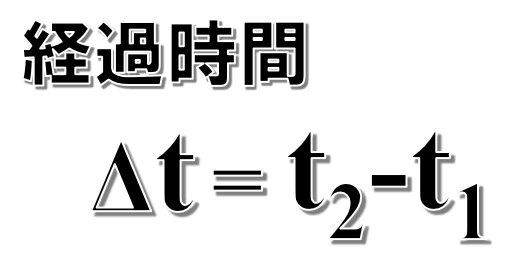
そして、速度の変化量をΔvとして、速度の変化量を計算すると

この時、速度の変化量を時間の変化量で割ると、1秒あたりの速度の変化量が求められます。


これが単位時間あたりの速度の変化量、つまり加速度になります。
こうして、求めた加速度を平均の加速度といいます。
加速度の単位は、m/s2 と書いてメートル毎秒毎秒と読みます。

SI単位系では、距離はメートル、時間は秒を基準とした単位を使用します。
したがって、1m/s2とは、1秒あたりに速度が1m/sの割合で増加する場合の加速度を意味しています。
加速度は、加速する場合もあれば減速する場合もあるので、大きさと向きを持つベクトル量に分類されます。
■平均の加速度の計算
ここで実際に平均の加速度の計算を確認してみます。
この場合であれば、時間の変化量は4.0、速度の変化量は3.0m/sから9.0m/sに変化しているので、次のようになります。
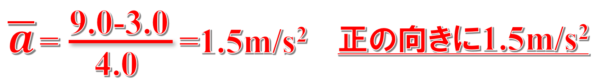
(2)一直線上を正の向きに8.0m/sの速度で進む物体が、6.0秒後に負の向きに4.0m/sの速度になった時

この場合は、少し注意が必要です。
最初に正の向きに8.0m/sで進んでいた物体の速度は、6.0秒後に負の向き、つまり逆向きに4.0m/sの速度になっています。
だから、ここでの速度の変化量は、-4.0-8.0で-12m/sです。したがって、平均の加速度は次のようになります。
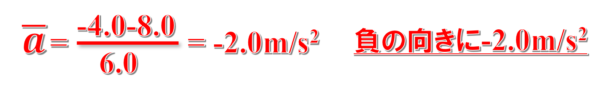
つまり1秒間に2.0m/sのペースで減速する加速度であるということです。
■加速度に関するv-tグラフ
次の表は、一直線上を静止した状態から動く物体の0.10秒後、0.20秒後、0.30秒後と、0.1秒刻みに到達距離を測定してまとめたものです。
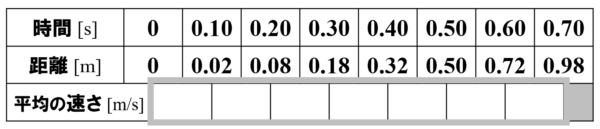
今から、この表に関するv-t グラフを作図してみます。
v-tグラフは、横軸に時間、縦軸に速度をとったグラフですが、表には速さや速度のデータがないので、時間と到達距離から平均の速さを求めていきます。
物体が動き始めてから、0.10秒までの平均の速さは、0.10分の0.02で0.2m/s、0.10秒から0.20秒の区間での平均の速さは、0.10分の0.08-0.02で0.6m/sです。
![]()
同じように計算していくと、次の区間からは、1.0m/s、1.4m/s、1.8m/s、2.2m/s、2.6m/s となります。
それぞれの時間間隔における平均の速さをまとめると、次のようになります。
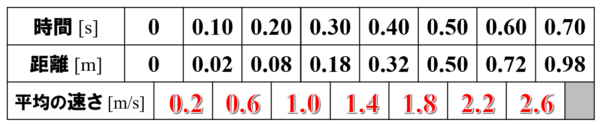
これをもとにして物体の運動のv-t図を作図します。
最初の0.10秒での平均の速さは0.20m/sなので、縦軸の0.2の位置から、横軸に平行な線を原点から0.1の区間に引きます。
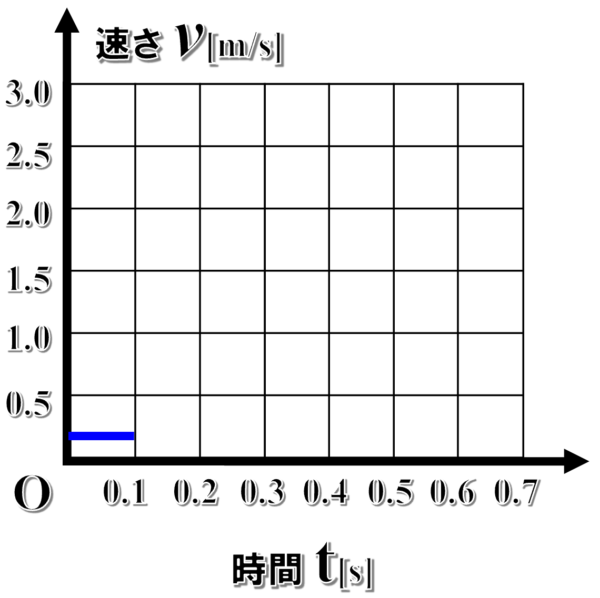
そして、0.1秒後から0.2秒後の平均の速さは、0.6m/sなので、さっきと同じように縦軸の0.6の位置から平行な線を引きます。
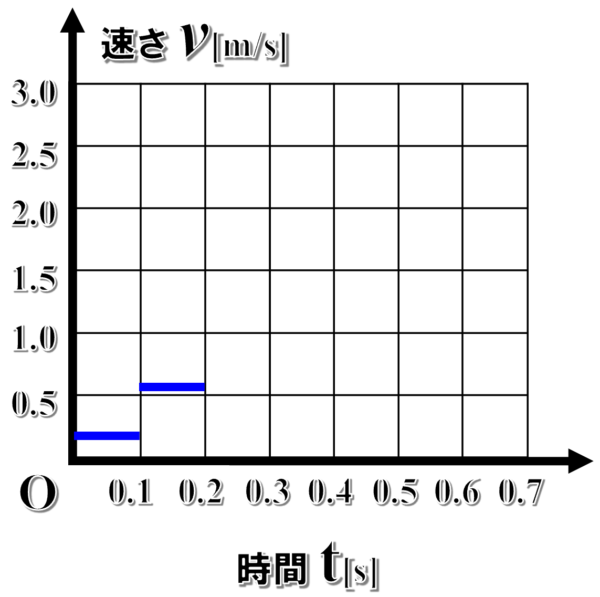
こうして、各区間での平均の速さに対応した線を引いていくと次のようになります。
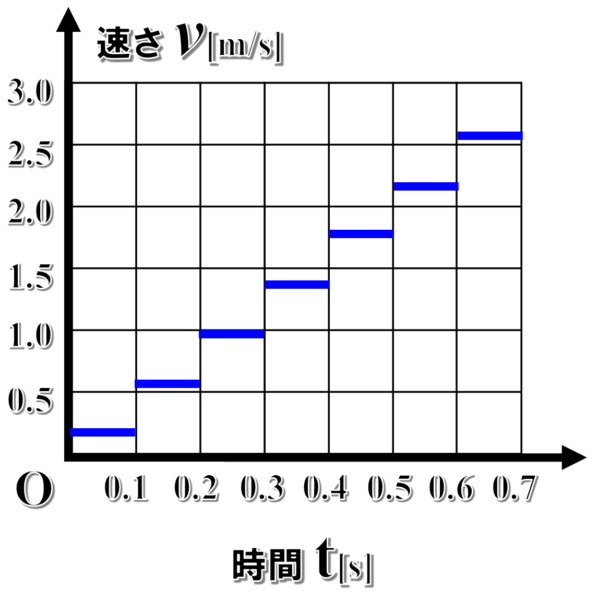
これが表のデータを忠実に再現したv-tグラフになります。
ただ、このグラフを実際の現象に当てはめて考えた時に、0.1秒になった瞬間に速さが瞬時に0.2m/sから0.6m/sに変化するのは不自然です。
そこで、1番で求めた速さを各時間の中央の時刻での速さと考えます。例えば、0.10から0.20秒での平均の速さは、時刻0.15秒での速さとみなして、横軸0.15の位置から縦軸0.6位置に点を書き込みます。
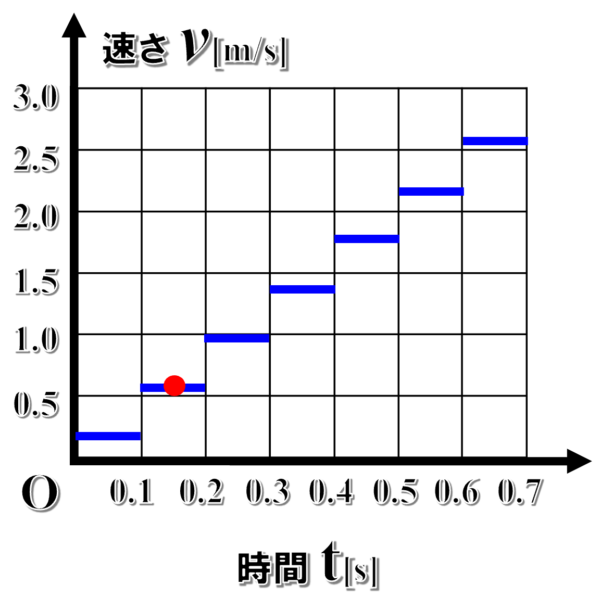
他の時刻についても同様に書き込んでいくと、このようになります。
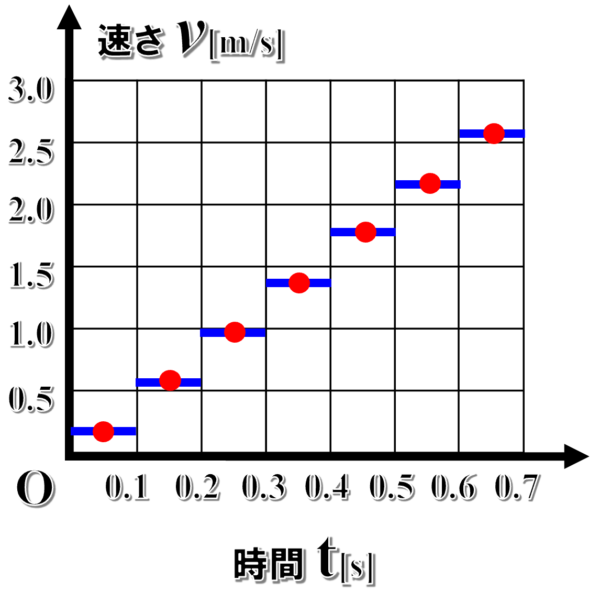
これらの点を結んで出来たグラフは、さっきよりも実際の現象に近いv-tグラフになります。
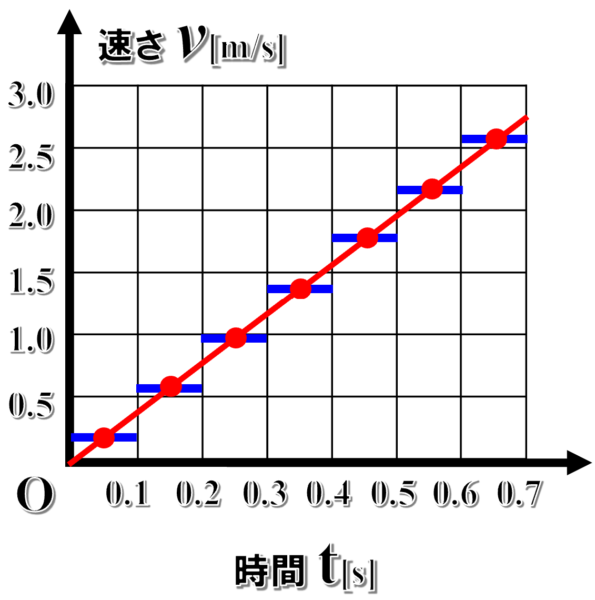
より厳密に加速度を求める場合は、計測する時間を短くしていきます。

そうして、計測時間を限りなく0秒に近づけていった時の加速度のことを瞬間の加速度といいます。
次にこのグラフから物体の加速度を求めてみます。

加速度を求める式は、Δt分のΔvでグラフ上の2点間の速度、ここでは速さの差を時間で割ったものになりますが、これはv-tグラフの傾きを求めること同じです。
したがって、グラフの傾きを求めることによって、物体の加速度を求めるという方針で進めていきます。
そうすると、グラフからtが0.50の時の値が2.0であることが読み取れます。

この数値を利用すると最も計算が簡単そうなので、こちら傾きを求めると、加速度aは、次のようになります。
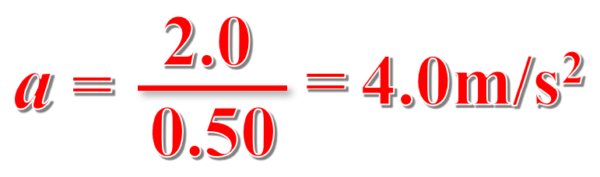
解説は以上となります。
次の記事
この単元の記事